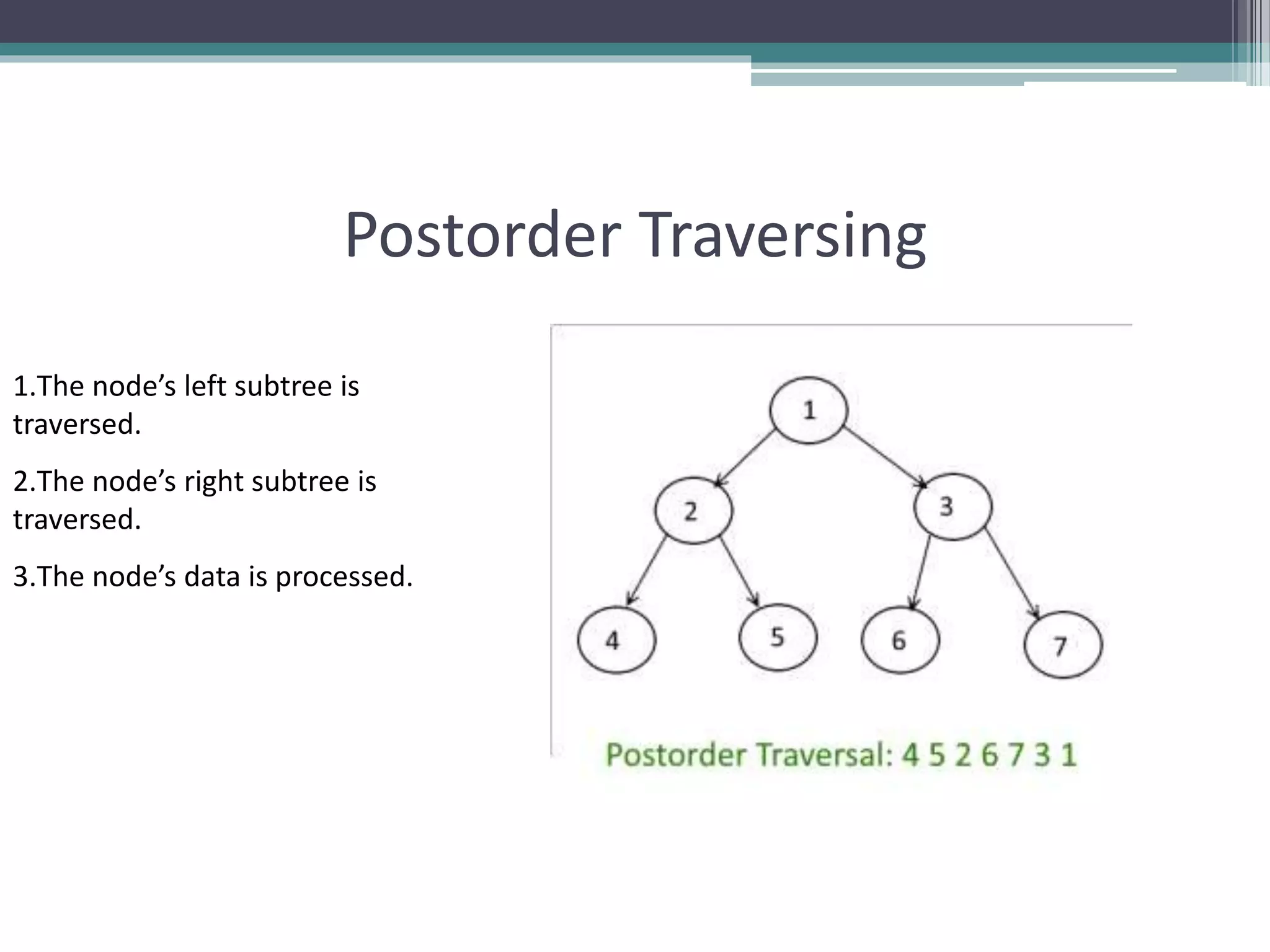
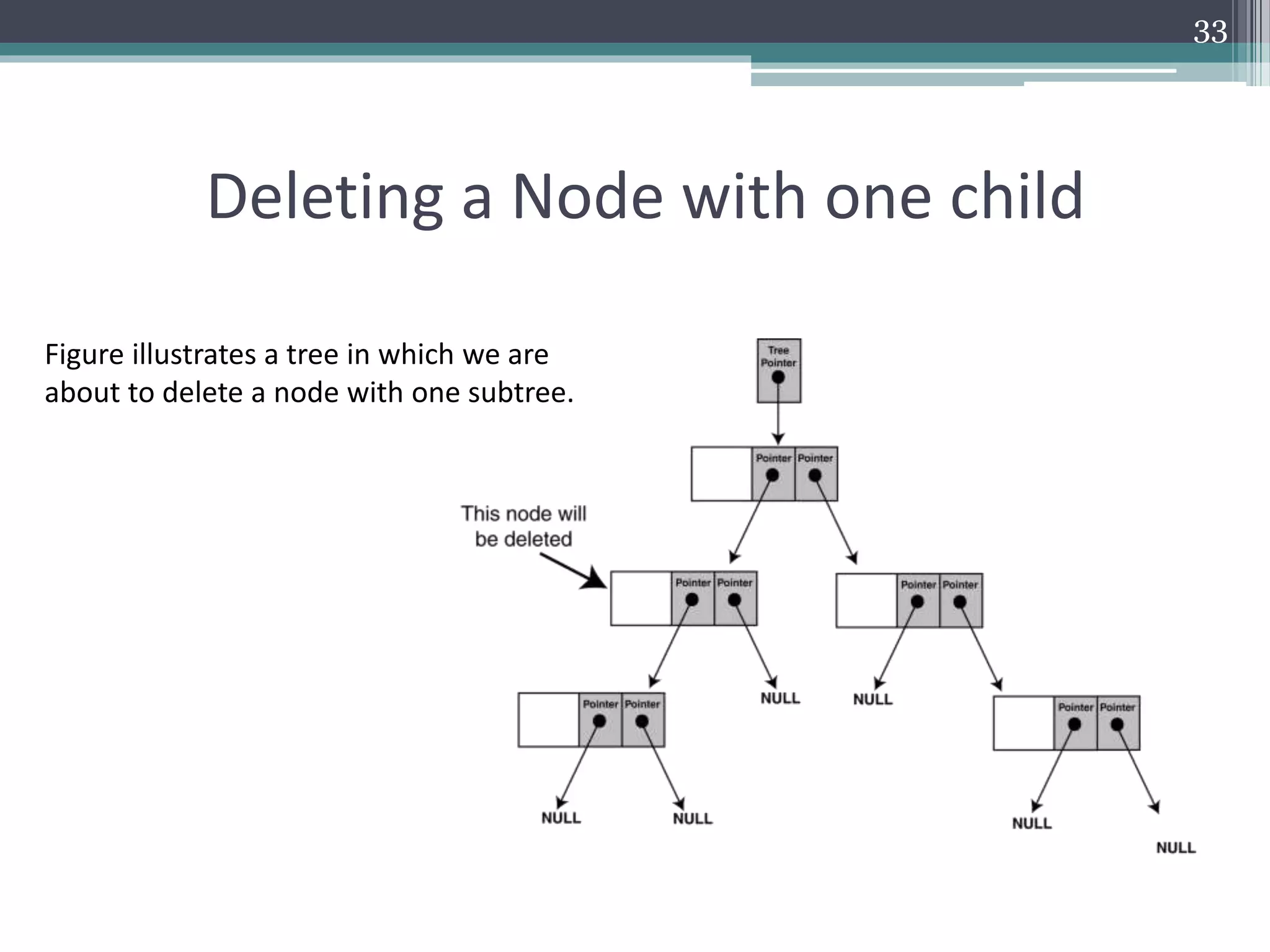
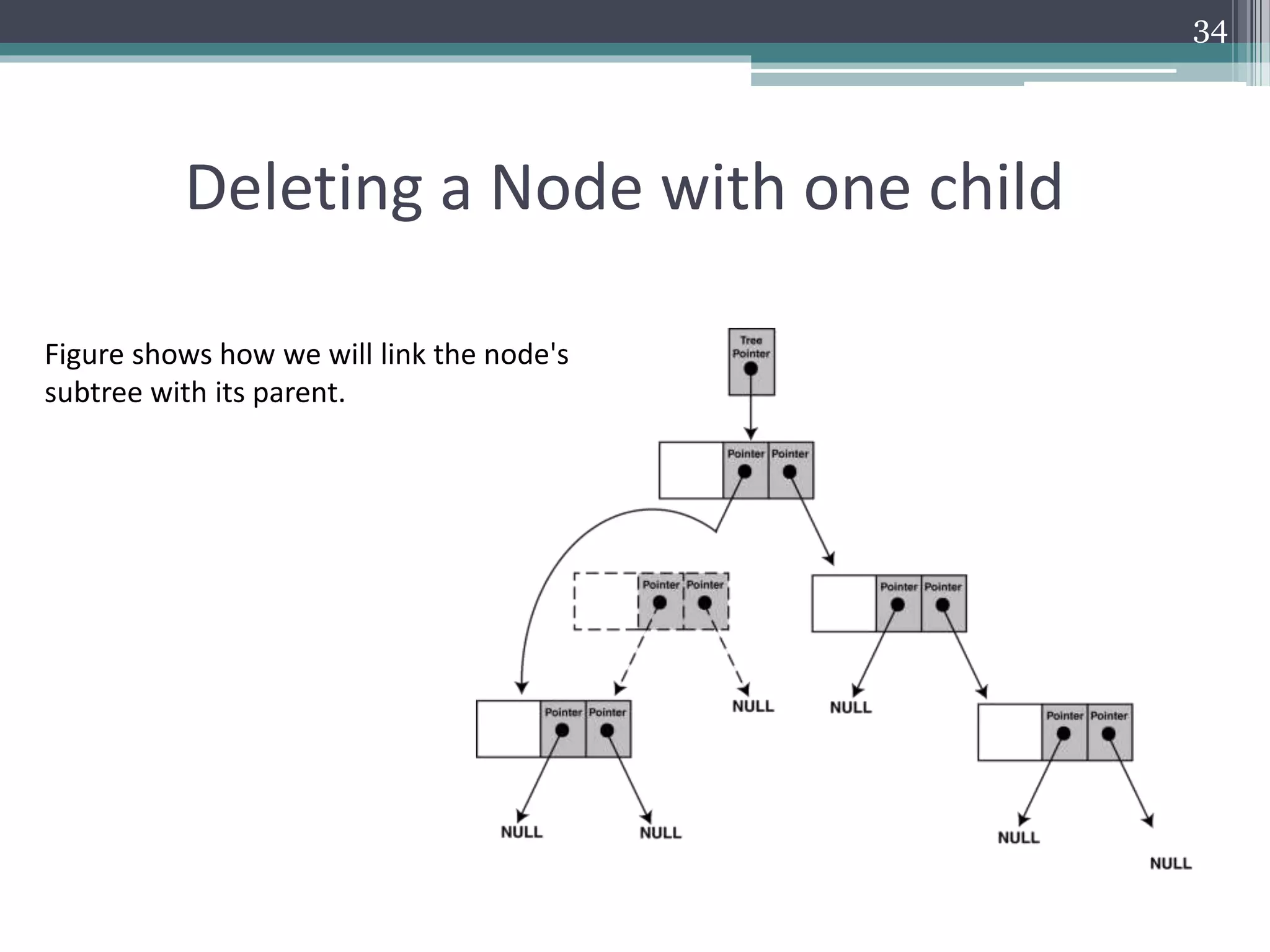
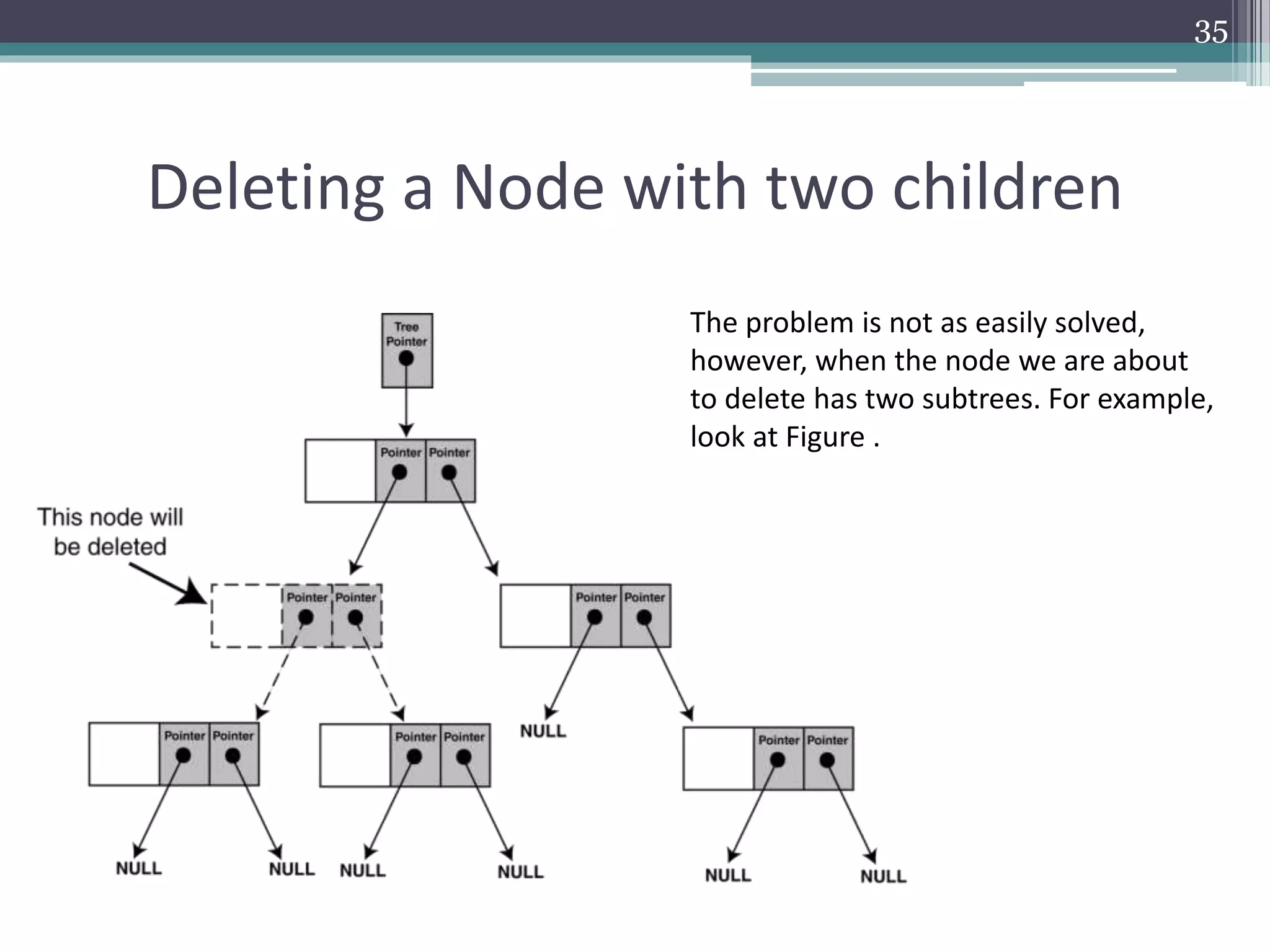
The document provides a comprehensive overview of binary trees, covering their structure, operations, and various traversal methods such as in-order, pre-order, and post-order. It also details explicit algorithms for inserting and deleting nodes in a binary search tree, as well as searching for elements within the tree. Additionally, it discusses special tree types including strictly binary trees and complete binary trees, offering a foundational understanding for programming applications.

1. Binary Tree
Prepared by: Afaq Mansoor Khan
BSSE III- Group A
Session 2017-21
IMSciences, Peshawar.

2. Last Lecture Summary
• Introduction to Queue Data Structure
• Types of Queue Data Structures
• Circular QUEUE and its Operations
• Double Ended QUEUE and its operations

3. Objectives Overview
• Introduction to Binary Tree
• Operations in Binary tree
• Recursive and Non Recursive Traversal of Binary/Binary
Search Tree
• In-Order Traversal
• Pre-Order Traversal
• Post-Order Traversal
• Insertion of New Node in BST
• Deletion of a Node from BST
• Searching in a Binary Search Tree

4. Introduction to Tree
• Fundamental data storage structures used in
programming.
• Combines advantages of an ordered array and a
linked list.
• Searching as fast as in ordered array.
• Insertion and deletion as fast as in linked list.

5. Computer Scientist’s View of a Tree
branches
leaves
root
nodes

6. Binary Tree
• Any Node can have maximum of two child nodes.
• Each node contains:
▫ A value (some sort of data item)
▫ A reference or pointer to a left child (may be null), and
▫ A reference or pointer to a right child (may be null)
• If not empty, a binary tree has a root node
▫ Every node in the binary tree is reachable from the root
node by a unique path
• A node with neither a left child nor a right child is called a leaf

7. Binary Tree
7
a
b c
d e
g h i
l
f
j k

8. Binary Tree
Strictly Binary Tree (SBT):
▫ Every Node has zero or two nodes.
▫ If (n -> LeafNode)
▫ then N=2n-1
Complete Binary Tree (CBT):
▫ All Leaf Nodes are at the same level.
▫ In CBT height of any leaf node is the height of the tree.
▫ N= 20 + 21 + 22 + 23 + ..… + 2L

9. Binary Tree Operations
Creating a Node:
• The basis of our binary tree node is the following
struct declaration:
9
struct TreeNode
{
int data;
TreeNode *left;
TreeNode *right;
TreeNode *parent
};
TreeNode *P=root;

10. Binary Tree Operations
• Root: if (P->parent==NULL)
• Leaf: if (P->Left==NULL && P->Right==NULL)
• isLeft (P){
▫ If ((P->Parent)->Left==P)
▫ return true; }
• isRight (P){
▫ If ((P->Parent)->Right==P)
▫ return true; }
• isSibling (P,Q){
▫ If ((P->Parent)==(Q->Parent))
▫ return true; }
10

11. 11
Tree Traversals
• A binary tree is defined recursively: it consists of a root, a
left subtree, and a right subtree
• To traverse the binary tree is to visit each node in the
binary tree exactly once
• Since a binary tree has three “parts,” there are six possible
ways to traverse the binary tree:
▫ root, left, right
▫ left, root, right
▫ left, right, root
▫ root, right, left
▫ right, root, left
▫ right, left, root

12. Traversing the Tree
• There are three simple ways to traverse a tree:
▫ Inorder
▫ Preorder
▫ Postorder
• Each of these methods is best implemented as a
recursive function.

13. 13
Inorder Traversing - Algorithm
1. Traverse the left subtree, i.e., call Inorder(left-
subtree)
2. Visit the root.
3. Traverse the right subtree, i.e., call
Inorder(right-subtree)

14. Inorder Traversing
1.The node’s left subtree is
traversed.
2.The node’s data is processed.
3.The node’s right subtree is
traversed.

15. 15
Inorder Traversing - Implementation
• In inorder, the root is visited in the middle
• Here’s an inorder traversal to print out all the
elements in the binary tree:
void inorderPrint(BinaryTree bt) {
inorderPrint(bt.leftChild);
cout<<bt.value;
inorderPrint(bt.rightChild);
}

16. Non Recursive Inorder Traversing
1) Create an empty stack S.
2) Initialize current node as root
3) Push the current node to S and set current = current->left
until current is NULL
4) If current is NULL and stack is not empty then:
a) Pop the top item from stack.
b) Print the popped item, set current = popped_item->right
c) Go to step 3.
5) If current is NULL and stack is empty then we are done.

17. 17
Uses of Inorder
• In case of binary search trees (BST), Inorder
traversal gives nodes in non-decreasing order. To
get nodes of BST in non-increasing order, a
variation of Inorder traversal where Inorder
traversals reversed can be used

18. 18
Preorder Traversing - Algorithm
1. Visit the root.
2. Traverse the left subtree, i.e., call
Preorder(left-subtree)
3. Traverse the right subtree, i.e., call
Preorder(right-subtree)

19. Preorder Traversing
1.The node’s data is processed.
2.The node’s left subtree is
traversed.
3.The node’s right subtree is
traversed.

20. 20
Preorder Traversing - Implementation
• In preorder, the root is visited first
• Here’s a preorder traversal to print out all the
elements in the binary tree:
void preorderPrint(BinaryTree bt) {
cout<<bt.value;
preorderPrint(bt.leftChild);
preorderPrint(bt.rightChild);
}

21. 21
Non Recursive Preorder Traversing
• Create a Stack.
• Print the root and push it to Stack and go left
i.e root=root.left and till it hits the NULL.
• If root is null and Stack is empty then
▫ return, we are done.
• Else
▫ Pop the top Node from the Stack and set it as, root
= popped_Node.
▫ Go right, root = root.right.
▫ Go to step 2.
• End If

22. 22
Uses of Preorder
• Preorder traversal is used to create a copy of the
tree.
• Preorder traversal is also used to get prefix
expression on of an expression tree.

23. 23
Postorder traversal - Algorithm
1. Traverse the left subtree, i.e., call
Postorder(left-subtree)
2. Traverse the right subtree, i.e., call
Postorder(right-subtree)
3. Visit the root.

24. Postorder Traversing
1.The node’s left subtree is
traversed.
2.The node’s right subtree is
traversed.
3.The node’s data is processed.

25. 25
Postorder traversal - Implementation
• In postorder, the root is visited last
• Here’s a postorder traversal to print out all the
elements in the binary tree:
void postorderPrint(BinaryTree bt) {
postorderPrint(bt.leftChild);
postorderPrint(bt.rightChild);
cout<<bt.value;
}

26. 26
Non Recursive Preorder Traversing
• Push root into Stack_One.
• while(Stack_One is not empty)
▫ Pop the node from Stack_One and push it into
Stack_Two.
▫ Push the left and right child nodes of popped node
into Stack_One.
• End Loop
• Pop out all the nodes from Stack_Two and print
it.

27. 27
Uses of Postorder
• Postorder traversal is used to delete the tree.
• Postorder traversal is also useful to get the postfix
expression of an expression tree.

28. Inserting a Node
• Inserting a Node: The idea is to do iterative level
order traversal of the given tree using queue. If
we find a node whose left child is empty, we
make new key as left child of the node. Else if we
find a node whose right child is empty, we make
new key as right child. We keep traversing the
tree until we find a node whose either left or
right is empty.
28

29. Inserting a Node - Algorithm
1. If the root is null:
a) Replace empty tree with a new tree with the item at the
root and return true
2. else if the item is equal to root.data
1. The item is already in the tree; return false
3. else if the item is less than root.data
1. Recursively insert the item in the left subtree
4. else
1. Recursively insert the item in the right subtree

30. Inserting a Node - Representation

31. Deleting a Node
• While deleting a leaf node we simply find its parent
and set the child pointer that links to it to NULL, and
then free the node's memory.
• But if we are deleting a node that has child nodes
then we must delete the node while at the same
time preserving the subtrees that the node links to.
• There are two possible situations when we are
deleting a non-leaf node:
▫ A) the node has one child, or
▫ B) the node has two children.
31

32. Deleting a Node - Algorithm
1. Starting at root, find the deepest and rightmost
node in binary tree and node which we want to
delete.
2. Replace the deepest rightmost node’s data with
node to be deleted.
3. Then delete the deepest rightmost node.

33. Deleting a Node with one child
33
Figure illustrates a tree in which we are
about to delete a node with one subtree.

34. Deleting a Node with one child
34
Figure shows how we will link the node's
subtree with its parent.

35. Deleting a Node with two children
35
The problem is not as easily solved,
however, when the node we are about
to delete has two subtrees. For example,
look at Figure .

36. Deleting a Node with two children
36
We cannot attach both of the node's subtrees
to its parent, so there must be an alternative
solution.
One way is to attach the node's right subtree
to the parent, and then find a position in the
right subtree to attach the left subtree. The
result is shown in Figure.

37. Deleting a Node
37
To delete a node from the IntBinaryTree, call the public member function
remove. The argument is the value of the node that is to be deleted.
void IntBinaryTree::remove(int num)
{
deleteNode(num, root);
}
The remove member function calls the deleteNode member function. It passes the
value of the node to delete, and the root pointer.

38. 38
Searching the Tree - Algorithm
1. if the root is null:
a) the item is not in the tree; return null
2. Compare the value of target with root.data
3. if they are equal:
a) the target has been found; return the data at the root
4. else if the target is less than root.data:
a) return the result of searching the left subtree
5. else:
a) return the result of searching the right subtree

39. 39
Searching Tree - Performance
• Search a tree is generally O(log n)
• If a tree is not very full, performance will be worse
• Searching a tree with only right subtrees, for example, is O(n)

40. Summary
• Introduction to Binary Tree
• Operations in Binary tree
• Recursive and Non Recursive Traversal of
Binary/Binary Search Tree
• In-Order Traversal
• Pre-Order Traversal
• Post-Order Traversal
• Insertion of New Node in BST
• Deletion of a Node from BST
• Searching in a Binary Search Tree

41. References
• https://www.geeksforgeeks.org/binary-tree-data-structure/
• www2.latech.edu/~box/ds/chap8.ppt
• https://www.slideshare.net/vanithachandru/binary-tree-24242122
• https://www.cs.cmu.edu/~adamchik/15-
121/lectures/Trees/trees.html
• https://www.slideshare.net/almario1988/binary-tree-7787268
• https://www.geeksforgeeks.org/binary-tree-data-structure/
• www2.latech.edu/~box/ds/chap8.ppt
• https://www.slideshare.net/vanithachandru/binary-tree-24242122
• https://www.cs.cmu.edu/~adamchik/15-
121/lectures/Trees/trees.html
• https://www.slideshare.net/almario1988/binary-tree-7787268