This document discusses linked lists and polynomials represented as linked lists. It provides details on singly linked lists, including how to implement insertion and deletion of nodes. It also describes how to represent stacks and queues as dynamically linked lists. Finally, it discusses representing polynomials using arrays or linked lists, and how to perform addition and multiplication of polynomials in each representation.

1. LINKED LIST
aND
ITS TYPES
Trupti Agrawal 1

2. LINKED LIST
In computer science, a linked list is a data structure consisting of a group
of nodes which together represent a sequence. Under the simplest form,
each node is composed of a data and a reference (in other words, a link) to
the next node in the sequence; more complex variants add additional links.
This structure allows for efficient insertion or removal of elements from
any position in the sequence.
Fig.: A linked list whose nodes contain two fields: an integer value and a
link to the next node. The last node is linked to a terminator used to signify
the end of the list.
Trupti Agrawal 2

3. Singly Linked Lists
Linked lists are drawn as an order sequence of nodes
with links represented as arrows (Figure 4.1).
The name of the pointer to the first node in the list is the name
of the list. (the list of Figure 4.1 is called ptr.)
 Notice that we do not explicitly put in the values of pointers, but simply
draw allows to indicate that they are there.
Trupti Agrawal 3

4. Singly Linked Lists [cont…]
The nodes do not resident in sequential locations
The locations of the nodes may change on different
runs
Link Field
Data Field
Node
. . . Null
ptr
chain
Trupti Agrawal 4

5. Singly Linked Lists [cont…]
Why it is easier to make arbitrary insertions and deletions using a linked
list?
To insert the word mat between cat can sat, we must:
 Get a node that is currently unused; let its address be paddr.
 Set the data field of this node to mat.
 Set paddr’s link field to point to the address found in the link field of
the node containing cat.
 Set the link field of the node containing cat to point to paddr.
Trupti Agrawal 5

6. Singly Linked Lists [cont…]
Delete mat from the list:
We only need to find the element that immediately precedes
mat, which is cat, and set its link field to point to mat’s link
(Figure 4.3).
We have not moved any data, and although the link field of
mat still points to sat, mat is no longer in the list.
Trupti Agrawal 6

7. Singly Linked Lists [cont…]
We need the following capabilities to make linked
representations possible:
Defining a node’s structure, that is, the fields it contains. We
use self-referential structures, discussed in Section 2.2 to do
this.
Create new nodes when we need them. (malloc)
Remove nodes that we no longer need. (free)
Trupti Agrawal 7

8. Singly Linked Lists [cont…]
2.2.4 Self-Referential Structures
One or more of its components is a pointer to itself.
typedef struct list {
char data;
list *link;
}
Construct a list with three nodes
item1.link=&item2;
item2.link=&item3;
malloc: obtain a node (memory)
free: release memory
list item1, item2, item3;
item1.data=‘a’;
item2.data=‘b’;
item3.data=‘c’;
item1.link=item2.link=item3.link=NULL;
a b c
Trupti Agrawal 8

9. Singly Linked Lists [cont…]
Example [List of words ending in at]:
Declaration
typedef struct list_node *list_pointer;
struct list_node {
char data [4];
list_pointer link;
};
Creation
list_pointer ptr =NULL;
Testing
#define IS_EMPTY(ptr) (!(ptr))
Allocation
ptr=(list_pointer) malloc (sizeof(list_node));
Return the spaces:
free(ptr); Trupti Agrawal 9

10. Singly Linked Lists [cont…]
e -> name  (*e).name
strcpy(ptr -> data, “bat”);
ptr -> link = NULL;
address of
first node
ptr data ptr link
 b a t 0 NULL
ptr
Figure 4.4:Referencing the fields of a node(p.142)
Trupti Agrawal 10

11. Singly Linked Lists [cont…]
Example 4.2 [Two-node linked list]:
typedef struct list_node *list_pointer;
typedef struct list_node {
int data;
list_pointer link;
};
list_pointer ptr =NULL;
Program 4.2: Create a two-node list
list_pointer create2( )
{
/* create a linked list with two nodes */
list_pointer first, second;
first = (list_pointer) malloc(sizeof(list_node));
second = (list_pointer) malloc(sizeof(list_node));
second -> link = NULL;
second -> data = 20;
ptr
first -> data = 10;
first ->link = second;
return first;
10 20
} #define IS_FULL(ptr) (!
(ptr))
When returns NULL if there
is no more memory.
 NULL
Trupti Agrawal 11

12. Singly Linked Lists [cont…]
• Insertion
Observation
 insert a new node with data = 50 into the list ptr after node
node
10 20
50
NULL
temp
ptr
Trupti Agrawal 12

13. Singly Linked Lists [cont…]
Implement Insertion:
void insert(list_pointer *ptr, List_pointer node)
{
/* insert a new node with data = 50 into the list ptr after
node */
list_pointer temp;
temp=(list_pointer)malloc(sizeof(list_node));
if(IS_FULL(temp)){
fprintf(stderr, “The memory is fulln”);
exit(1);
}
temp->data=50;
temp 50
Trupti Agrawal 13

14. Singly Linked Lists [cont…]
if(*ptr){ //nonempty list
temp->link = node->link;
node->link = temp;
}
else{ //empty list
temp->link = NULL;
*ptr = temp;
}
}
node
10 20
50
NULL
temp
ptr
Trupti Agrawal 14

15. Singly Linked Lists [cont…]
Deletion
Observation: delete node from the list
ptr trial node
10 50 20 NULL
ptr trial node
10 50 20 NULL
ptr
10 20 NULL
Trupti Agrawal 15

16. Singly Linked Lists [cont…]
Implement Deletion:
void delete(list_pointer *ptr, list_pointer trail,
list_pointer node)
{
/* delete node from the list, trail is the preceding node
ptr is the head of the list */
if(trail)
trail->link = node->link;
else
*ptr = (*ptr)->link;
free(node);
}
ptr trial node
10 50 20 NULL
Trupti Agrawal 16

17. Singly Linked Lists [cont…]
Print out a list (traverse a list)
Program 4.5: Printing a list
void print_list(list_pointer ptr)
{
printf(“The list contains: “);
for ( ; ptr; ptr = ptr->link)
printf(“%4d”, ptr->data);
printf(“n”);
}
Trupti Agrawal 17

18. Dynamically Linked Stacks and Queues
When several stacks and queues coexisted, there was no
efficient way to represent them sequentially.
Notice that direction of links for both stack and the queue
facilitate easy insertion and deletion of nodes.
 Easily add or delete a node form the top of the stack.
 Easily add a node to the rear of the queue and add or delete a node at the
front of a queue.
Trupti Agrawal 18

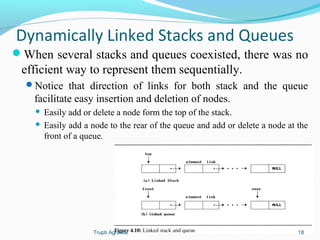
19. Dynamically Linked
Stacks and Queues [cont…]
Represent n stacks
top item link
link
...
NULL
Stack
Trupti Agrawal 19

20. Dynamically Linked
Stacks and Queues [cont…]
Push in the linked stack
void add(stack_pointer *top, element item){
/* add an element to the top of the stack */ Push
stack_pointer temp = (stack_pointer) malloc (sizeof (stack));
if (IS_FULL(temp)) {
fprintf(stderr, “ The memory is fulln”);
exit(1);
}t
emp->item = item;
temp->link = *top;
*top= temp;
}
temp item link
top link
link
...
NULL
Trupti Agrawal 20

21. Dynamically Linked
Stacks and Queues [cont…]
• Pop from the linked stack
element delete(stack_pointer *top) {
/* delete an element from the stack */ Pop
stack_pointer temp = *top;
element item;
if (IS_EMPTY(temp)) {
fprintf(stderr, “The stack is emptyn”);
exit(1);
}i
tem = temp->item;
*top = temp->link;
free(temp);
return item;
}
item link
link
link
...
NULL
temp
top
Trupti Agrawal 21

22. Dynamically Linked
Stacks and Queues [cont…]
Represent n queues
front item link
link
...
NULL
Queue
rear
Delete from
Add to
Trupti Agrawal 22

23. Dynamically Linked
Stacks and Queues [cont…]
enqueue in the linked queue
front link
...
NULL
temp item
link
rear
NULL
Trupti Agrawal 23

24. Dynamically Linked
Stacks and Queues [cont…]
dequeue from the linked queue (similar to push)
front item link
link
link
...
NULL
temp
rear
Trupti Agrawal 24

25. Dynamically Linked
Stacks and Queues [cont…]
The solution presented above to the n-stack, m-queue
problem is both computationally and
conceptually simple.
We no longer need to shift stacks or queues to make
space.
Computation can proceed as long as there is memory
available.
Trupti Agrawal 25

26. Polynomials
A polynomial is an expression that contains more than two
terms. A term is made up of coefficient and exponent. An
example of polynomial is
P(x) = 4x3+6x2+7x+9
Trupti Agrawal 26

27. Polynomials [cont…]
A polynomial thus may be represented using arrays or linked
lists.
Array representation assumes that the exponents of the given
expression are arranged from 0 to the highest value (degree),
which is represented by the subscript of the array beginning
with 0. The coefficients of the respective exponent are placed
at an appropriate index in the array. The array representation
for the above polynomial expression is given below:
Trupti Agrawal 27

28. Polynomials [cont…]
A polynomial may also be represented using a linked list. A
structure may be defined such that it contains two parts- one is
the coefficient and second is the corresponding exponent. The
structure definition may be given as shown below:
ccooeeff eexxppoonn lliinnkk
 struct polynomial
{i
nt coefficient;
int exponent;
struct polynomial *next;
};
Trupti Agrawal 28

29. Polynomials [cont…]
Thus the above polynomial may be represented
using linked list as shown below:
Trupti Agrawal 29

30. Polynomials [cont…]
Addition of two Polynomials:
o For adding two polynomials using arrays is straightforward method, since both the arrays
may be added up element wise beginning from 0 to n-1, resulting in addition of two
polynomials.
o Addition of two polynomials using linked list requires comparing the exponents, and
wherever the exponents are found to be same, the coefficients are added up. For terms with
different exponents, the complete term is simply added to the result thereby making it a
part of addition result.
Multiplication of two Polynomials:
o Multiplication of two polynomials however requires manipulation of each node such that
the exponents are added up and the coefficients are multiplied.
o After each term of first polynomial is operated upon with each term of the second
polynomial, then the result has to be added up by comparing the exponents and adding the
coefficients for similar exponents and including terms as such with dissimilar exponents in
the result.
Trupti Agrawal 30

31. Polynomials [cont…]
Attach a node to the end of a list
void attach(float coefficient, int exponent, poly_pointer *ptr){
/* create a new node with coef = coefficient and expon = exponent, attach
it to the node pointed to by ptr. Ptr is updated to point to this new node
*/
poly_pointer temp;
temp = (poly_pointer) malloc(sizeof(poly_node));
/* create new node */
if (IS_FULL(temp)) {
fprintf(stderr, “The memory is fulln”);
exit(1);
}
temp->coef = coefficient; /* copy item to the new node */
temp->expon = exponent;
(*ptr)->link = temp; /* attach */
*ptr = temp; /* move ptr to the end of the list */
} Trupti Agrawal 31

32. Polynomials [cont…]
 Analysis of PADD (Polynomial addition)
f f
e e
m A x = a x m- + ××× + a x + B x = b x n- + + b x
( )( 1 0 ) ( )( 1 0 )
- - 
n
1 0 1 0
1. coefficient additions
0 £ additions £ min(m, n)
where m (n) denotes the number of terms in A (B).
2. exponent comparisons extreme case:
em-1 > fm-1 > em-2 > fm-2 > … > e1 > f1 > e0 > f0
m+n-1 comparisons
3. creation of new nodes extreme case: maximum number of
terms in d is m+n m + n new nodes
summary: O(m+n)
Trupti Agrawal 32

33. Polynomials [cont…]
A Suite for Polynomials
e(x) = a(x) * b(x) + d(x)
poly_pointer a, b, d, e;
...
a = read_poly();
b = read_poly();
d = read_poly();
temp = pmult(a, b);
e = padd(temp, d);
print_poly(e);
read_poly()
print_poly()
padd()
psub()
pmult()
temp is used to hold a partial result.
By returning the nodes of temp, we
may use it to hold other polynomials
Trupti Agrawal 33

34. Polynomials [cont…]
Erase Polynomials
erase frees the nodes in temp
void erase (poly_pointer *ptr){
/* erase the polynomial pointed to by ptr */
poly_pointer temp;
while ( *ptr){
temp = *ptr;
*ptr = (*ptr) -> link;
free(temp);
}
}
Trupti Agrawal 34

35. Circularly Linked Lists
Circular Linked list
The link field of the last node points to the first node in
the list.
Example
Represent a polynomial ptr = 3x14+2x8+1 as a circularly
linked list.
ptr 33 1144 22 88 11 00
Trupti Agrawal 35

36. Circularly Linked Lists [cont…]
Maintain an Available List
We free nodes that are no longer in use so that we may
reuse these nodes later
We can obtain an efficient erase algorithm for circular
lists, by maintaining our own list (as a chain) of nodes
that have been “freed”.
Instead of using malloc and free, we now use get_node
(program 4.13) and ret_node (program 4.14).
avail ... NULL
List of freed nodes
Trupti Agrawal 36

37. Circularly Linked Lists [cont…]
Maintain an Available List (cont’d)
When we need a new node, we examine this list.
If the list is not empty, then we may use one of its nodes.
Only when the
list is empty we
do need to use
malloc to
create a new
node.
Trupti Agrawal 37

38. Circularly Linked Lists [cont…]
Maintain an Available List (cont’d)
Insert ptr to the front of this list
Let avail be a variable of type poly_pointer that points
to the first node in our list of freed nodes.
Henceforth, we call this list the available space list or
avail list.
Initially, we set avail to NULL
Trupti Agrawal 38

39. Circularly Linked Lists [cont…]
Maintain an Available List
Erase a circular list in a fixed
amount (constant) of time
O(1) independent of the
number of nodes in the list
using cerase
     
temp
ptr
avail      N U LL
Trupti Agrawal 39

40. Circularly Linked Lists [cont…]
We must handle the zero polynomial as a special
case. To avoid it, we introduce a head node into each
polynomial
each polynomial, zero or nonzero, contains one additional
node.
The expon and coef fields of this node are irrelevant.
Why ?
So !
Trupti Agrawal 40

41. Circularly Linked
Lists [cont…]
For fit the
circular list with
head node
representation
We may remove
the test for (*ptr)
from cerase
Changes the
original padd to
cpadd
/* head node */
/*a->expon=-1, so b->expont > -1 */
/* link to the first node */
Trupti Agrawal 41

42. Circularly Linked Lists [cont…]
Operations for circularly linked lists
Question:
What happens when we want to insert a new node at the
front of the circular linked list ptr?
ptr x1 x2 x3
Answer:
 move down the entire length of ptr.
Possible Solution:
x1 x2 x3 ptr
Trupti Agrawal 42

43. Circularly Linked Lists [cont…]
 Insert a new node
at the front of a
circular list
 To insert node at
the rear, we only
need to add the
additional
statement *ptr =
node to the else
clause of
insert_front
x1 x2 x3 ptr
node
Trupti Agrawal 43

44. Circularly Linked Lists [cont…]
Finding the length of a circular list
Trupti Agrawal 44

45. Doubly Linked Lists [cont…]
Singly linked lists pose problems because we can
move easily only in the direction of the links
Doubly linked list has at least three fields
left link field(llink), data field(item), right link
field(rlink).
The necessary declarations:
typedef struct node *node_pointer;
typedef struct node{
node_pointer llink;
element item;
node_pointer rlink;
};
... NULL
? ptr
Trupti Agrawal 45

46. Doubly Linked Lists [cont…]
Sample
doubly linked circular with head node: (Figure 4.23)
empty double linked circular list with head node
(Figure 4.24)
suppose that ptr points to any node in a doubly
linked list, then:
 ptr = ptr -> llink -> rlink = ptr -> rlink -> llink
Trupti Agrawal 46

47. Doubly Linked Lists [cont…]
Insert node
Head node
llink item rlink
New node
node
Trupti Agrawal 47

48. Doubly Linked Lists [cont…]
Delete node
Head node
llink item rlink
deleted node
Trupti Agrawal 48

49. THANK YOU….. !!!
Trupti Agrawal 49