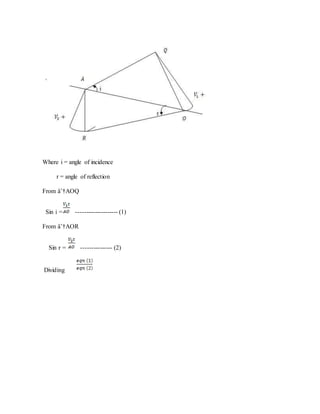
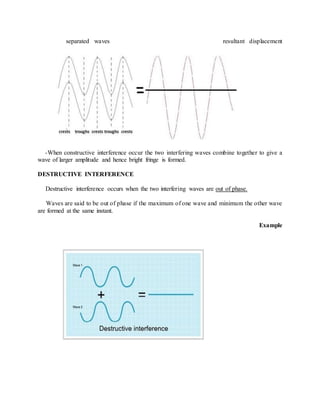
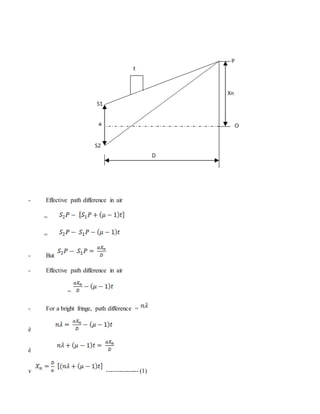
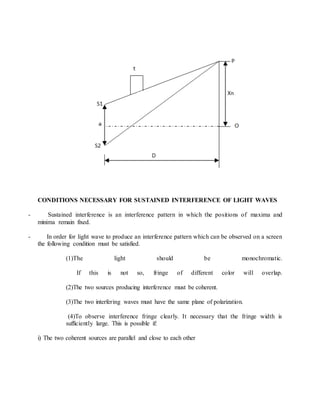
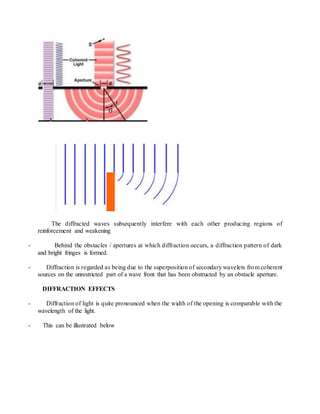
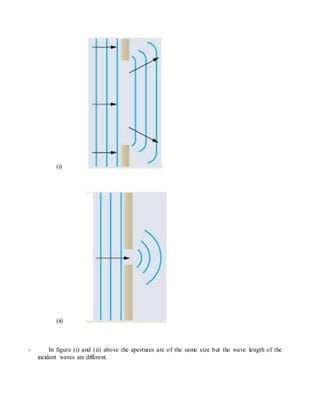
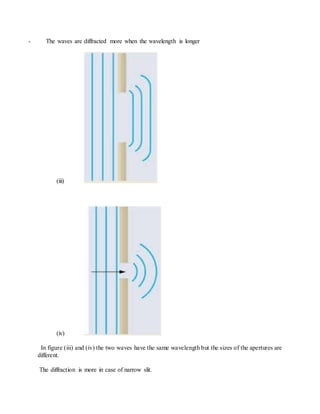
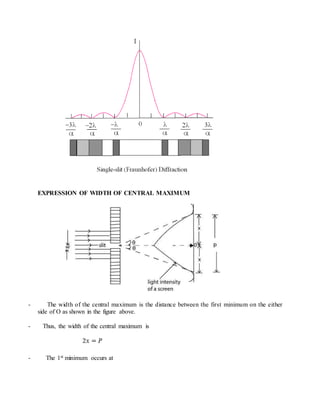
This document describes the theory behind Young's double slit experiment. It defines key terms like coherent sources, constructive and destructive interference, and how they relate to the bright and dark fringes observed in the interference pattern. It presents the mathematical equations that describe the displacement and width of the fringes based on the slit separation, wavelength of light, and distance to the viewing screen. Several sample problems are also provided to demonstrate how to use these equations to calculate values related to the experimental setup and observed interference patterns.