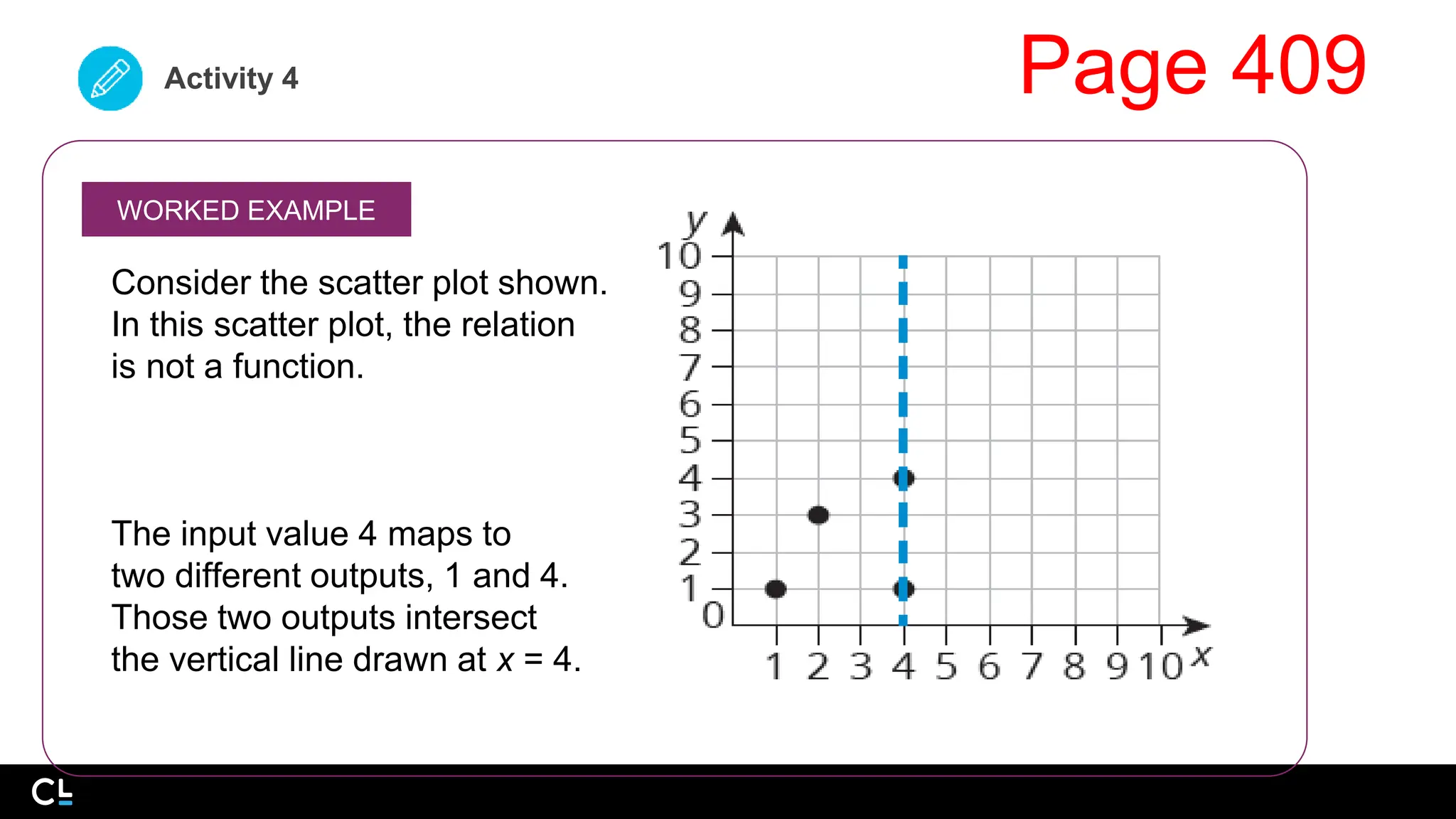
The document provides information about functions and how to determine if a relation represents a function. It discusses functions in terms of mappings, ordered pairs, graphs, and equations. Key points covered include: - A function is a relation where each input has exactly one output. To determine if a relation is a function, check for repeated x-values. - The vertical line test can be used to determine if a graph is a function - if any vertical line intersects the graph at more than one point, it is not a function. - Equations can also represent functions, and this can be tested by substituting values for x and checking if each x has a single y-value output.

1. PRIMETIME
Is the given relation below a function?
Explain.
{(0, 1), (2,4), (5,7), (3, 5) , ( 3, 6)}
Answer: No. It is not a function.
The x value 3 is assigned to 5 and 6.

2. • Describe a functional relationship in terms of a
rule which assigns to each input exactly one
output.
Learning Goals
• Determine whether a relation (represented as a
mapping, set of ordered pairs, table, sequence,
graph, equation, or context) is a function.

3. A function is a relation which describes that there
should be only one output for each __________.
To identify a function from a relation, check to see if
any of the ___________ values are repeated - if not,
it is a function.

4. Activity 4
Functions as Graphs
The vertical line test is a visual method used
to determine whether a relation represented
as a graph is a function. To apply the vertical
line test, consider all of the vertical lines you
can draw on the graph of a relation. When
any vertical line intersects the graph at more
than one point, the relation is not a function.
Page 409

5. Activity 4
WORKED EXAMPLE
Consider the scatter plot shown.
In this scatter plot, the relation
is not a function.
The input value 4 maps to
two different outputs, 1 and 4.
Those two outputs intersect
the vertical line drawn at x = 4.
Page 409

6. Activity 4
1. Use the definition of function to explain why the
vertical line test works.
Look back at the
graphs of the
sequences in the
lesson Patterns,
Sequences,
Rules....
Which sequences
are functions?
TAKE NOTE...
Page 409

7. 2. Use the 12 cards that you sorted in the previous
lesson. Sort the graphs into two groups: functions
and non-functions. Use the letter of each graph to
record your findings.
Page 409
5 minutes

8. Page 397

10. 2. Use the 12 cards that you sorted in the previous
lesson. Sort the graphs into two groups: functions
and non-functions. Use the letter of each graph to
record your findings.
Page 409

11. Activity 5
Functions as Equations
So far, you have determined whether a
mapping, context, or a graph represents a
function. You can also determine whether
an equation is a function.

12. Activity 5
WORKED EXAMPLE
You can use the equation y = 3x to convert yards to feet. Let x
represent the number of yards, and let y represent the number of feet.
You can use the equation y = 3x to convert yards to feet. Let x
represent the number of yards, and let y represent the number of feet.
To test whether this equation is
a function, first, substitute values
for x into the equation, and then
determine whether any x-value maps
to more than one y-value. When
each x-value has exactly one y-value,
it is a function. Otherwise, it is not
a function.
In this case, every x-value maps to only one y-value. You multiply each
x-value by 3. Therefore, this equation is a function.
Page 410

13. Activity 5
It is impossible to test every possible input value to determine whether or not the
equation represents a function. You can graph any equation to see the pattern and
use the vertical line test to determine whether it represents a function.
1. Determine whether each equation is a function. List three ordered pairs that
are solutions to each. Explain your reasoning.
a) y = 5x + 3
b) y = x2
c) y = |x|
d) x2 + y2 = 1
e) y = 4
f) x = 2
If you do not
recognize the
graph, use a
graphing calculator
to see the pattern.
THINK ABOUT...

14. Page 410

17. EXIT TICKET
QUIZZZ