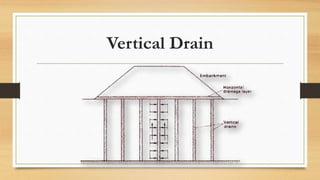
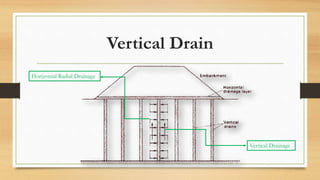
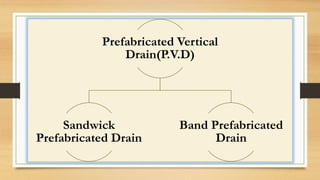
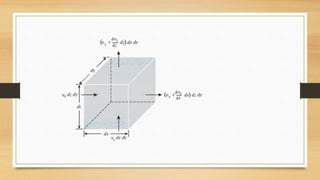
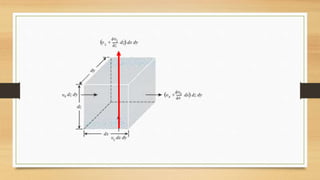
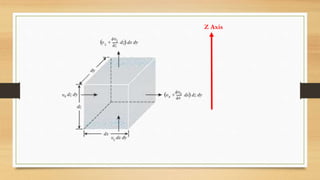
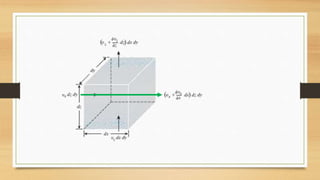
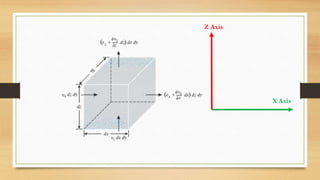
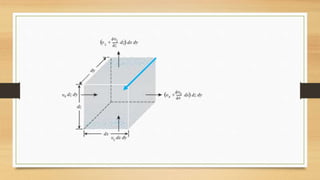
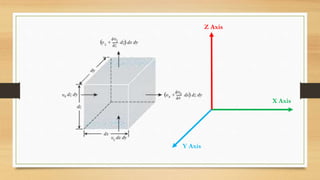
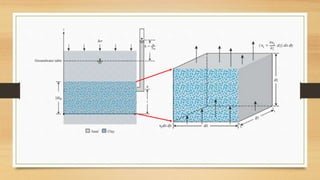
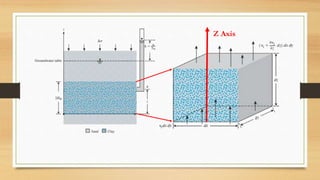
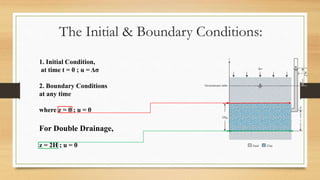
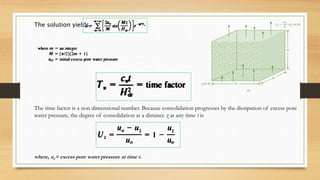
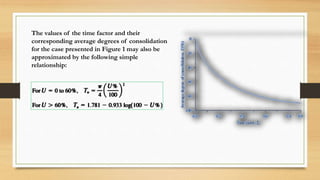
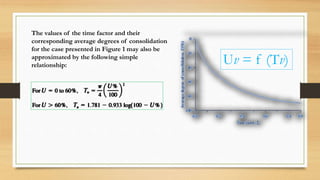
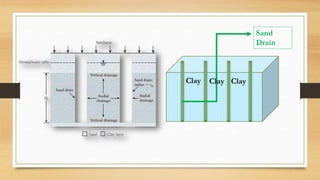
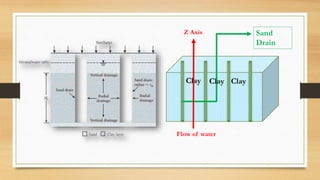
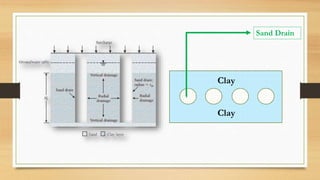
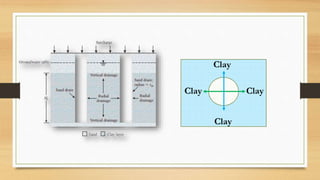
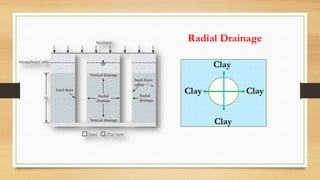
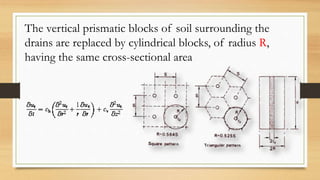
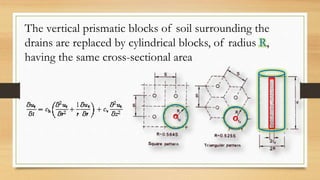
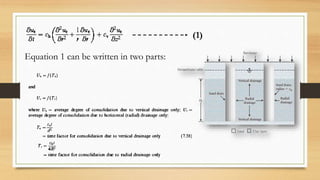
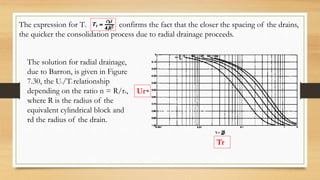
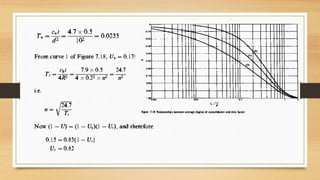
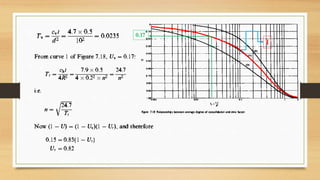
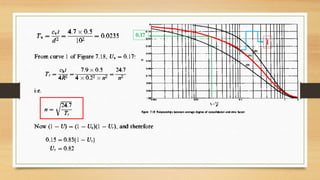
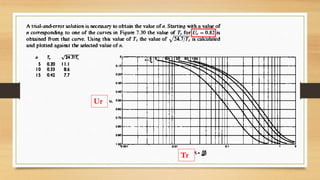
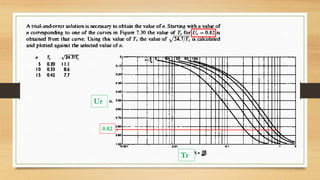
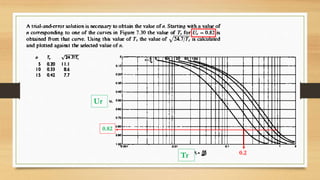
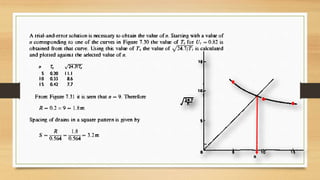
This document discusses vertical drains, which are used to accelerate consolidation in saturated clays. It describes how vertical drains work by shortening drainage paths within clay. Common installation methods involve creating boreholes and placing vertical drains made of sand or prefabricated materials like sandwick or band drains. Design considerations for vertical drains include drain spacing, fill height, soil permeability, and achieving a desired consolidation level within a given time. Mathematical equations are provided for analyzing consolidation based on Terzaghi's theory involving factors like coefficient of consolidation and excess pore water pressure. An example problem demonstrates calculating degree of consolidation over time for a layered soil system using vertical drains.