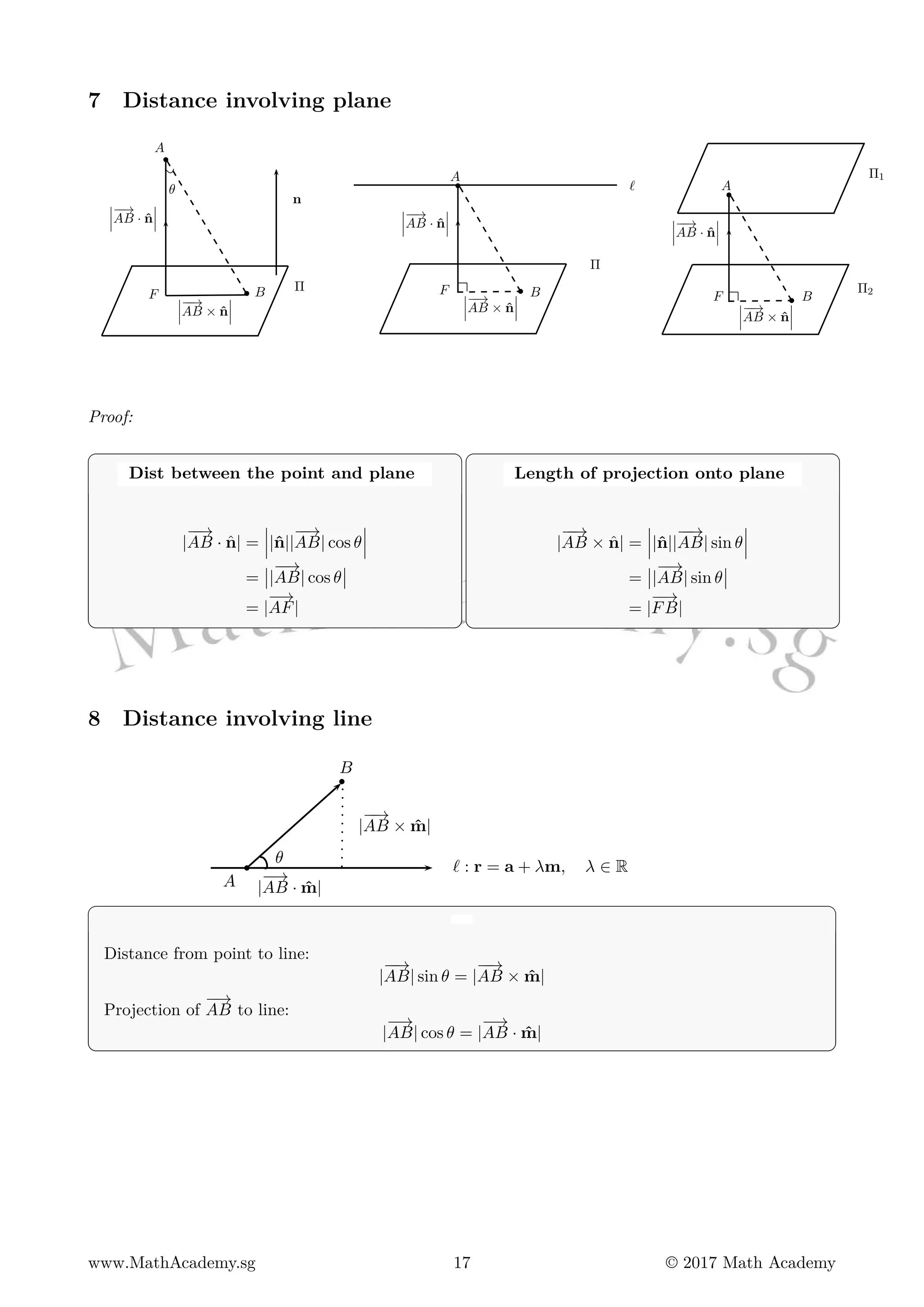
The document discusses various topics related to vectors and planes:
1. It explains the vector product in three forms - mathematical calculation, 3D picture, and in terms of sine. It provides an example to calculate the vector product of two vectors.
2. It discusses the different forms of the equation of a plane - parametric, scalar product, and Cartesian forms. It provides examples to write the equation of a plane in these different forms.
3. It explains how to find the foot of the perpendicular from a point to a plane. It provides examples to find the foot and shortest distance.
4. It discusses how to find acute angles between lines, planes, and a line and plane. Examples



![(b) The plane Π contains the point A(2, 2, −2) and the line r =
1
3
−3
+ λ
−2
0
1
, λ ∈ R.
Find the equation of Π1 in scalar product form.
[r ·
1
3
2
= 4]
(c) Find the cartesian equation of the following planes:
(i) x − y plane
x
y
z
(ii) x − z plane
x
y
z
(iii) y − z plane
x
y
z
(d) Given the following equation,
r ·
1
3
2
= 4,
how do we create points that lies on the plane?
How do we check if a point lies on a plane?
www.MathAcademy.sg 4 © 2017 Math Academy](https://image.slidesharecdn.com/vectors2-171220220503/75/Vectors2-4-2048.jpg)

![Example 4.
The point P has position vector i + 2j - k and a plane Π has equation Π : x + 2y + 3z = 16. Let A
be the point with position vector 9i + 2j + k.
(i) Find the foot of perpendicular from P to Π.
(ii) Hence, find the shortest distance between P and Π.
(iii) Show that A lies on the plane Π.
(iv) Let ℓ be the line that passes through A and P. Find the vector equation of the reflection of the
line ℓ in the plane Π.
[(i)
−−→
OF =
2
4
2
(ii)
√
14]
www.MathAcademy.sg 6 © 2017 Math Academy](https://image.slidesharecdn.com/vectors2-171220220503/75/Vectors2-6-2048.jpg)


![Example 5.
Find the ACUTE angle between the following two lines:
ℓ1 : r = (λ − 3)i + (2λ − 1)j + (2λ − 1)k, λ ∈ R.
ℓ2 : r = (3µ − 1)i + (2µ − 1)j + (µ − 1)k, µ ∈ R.
[36.7◦]
Example 6.
Find the acute angle between the line r = (i + 2j − k) + λ(i − j + k) and plane 2x − y + z = 4.
[70.5◦]
Example 7.
Find the acute angle between the planes r · (i + j + k) = 3 and r · (2i + 2j − k) = 1. [54.7◦]
www.MathAcademy.sg 9 © 2017 Math Academy](https://image.slidesharecdn.com/vectors2-171220220503/75/Vectors2-9-2048.jpg)

![Example 8.
(a) Determine the relationship between pairs of lines and planes:
(i) ℓ1 : r =
1
2
2
+ λ
2
−1
−1
and Π1 : r ·
1
1
1
= 5
(ii) ℓ2 : r = (i + j + k) + λ(i − 2j + k) and Π2 : r · (i + j + k) = 5
(b) Show that the line ℓ1 : r =
1
2
2
+ λ
2
−1
−1
intersects the plane r ·
1
0
1
= 2 at only 1 point.
[(ii) Parallel but does not lie in plane ]
Solution:
(i) m · n =
2
−1
−1
·
1
1
1
= 2 − 1 − 1 = 0. Therefore, ℓ1 and Π1 are parallel.
Furthermore, since
1
2
2
·
1
1
1
= 1 + 2 + 2 = 5, ℓ1 lies in Π1.
Alternative Method:
Since
1 + 2λ
2 − λ
2 − λ
·
1
1
1
= 1 + 2λ + 2 − λ + 2 − λ = 5, ∴ ℓ1 lies in Π1.
www.MathAcademy.sg 11 © 2017 Math Academy](https://image.slidesharecdn.com/vectors2-171220220503/75/Vectors2-11-2048.jpg)




![Example 11 (2011/YJC/Prelim/I/10modified).
The planes π1 and π2 have equations r · (2i − k) = 3 and r · (−i + 3j) = 2 respectively. The 2 planes
intersect in a line l.
(i) Find a vector equation of l. [2]
(ii) Find the coordinates of the point Q which is the reflection of the point P(5, −2, 7) in π2. [4]
(iii) It is given that P lies on π1. Hence or otherwise, find a vector equation of the reflection of the
plane π1 in π2. [2]
[(i) r =
3
2
7
6
0
+ t
3
1
6
, t ∈ R (ii) (2.4, 5.8, 7) (iii) r =
3
2
7
6
0
+ s
3
1
6
+ t
− 9
10
−139
30
−7
, s, t ∈ R]
www.MathAcademy.sg 16 © 2017 Math Academy](https://image.slidesharecdn.com/vectors2-171220220503/75/Vectors2-16-2048.jpg)

![Example 13.
Show the the line ℓ1 : r = 2i − 2j + 3k + λ(i − j + 4k) is parallel to the plane Π : r · (i + 5j + k) = 5.
Find the distance between them. [ 10√
27
units]
www.MathAcademy.sg 19 © 2017 Math Academy](https://image.slidesharecdn.com/vectors2-171220220503/75/Vectors2-19-2048.jpg)
![Example 14 (2011/VJC/Prelim/I/12).
The position vectors of points A, B, C and D with respect to the origin O are −2i + 5j + 5k, 3i + j +
4k, 3i − 4j + k and i + j − 5k respectively.
(i) Obtain an equation of the plane Π, containing A, B and C in the r · n = p form.
(ii) Calculate the angle between Π and the line joining A and D. Hence, or otherwise, find the
shortest distance of D from Π.
[(a) r.
7
15
−25
= −64 (b) 39.0◦, 7.04 units ]
www.MathAcademy.sg 20 © 2017 Math Academy](https://image.slidesharecdn.com/vectors2-171220220503/75/Vectors2-20-2048.jpg)

