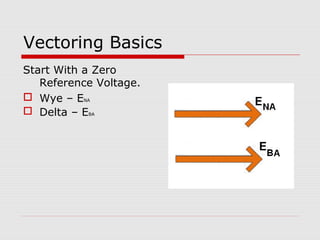
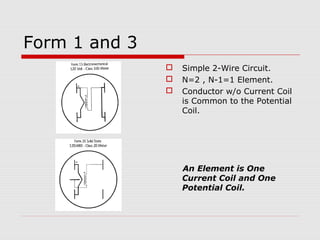
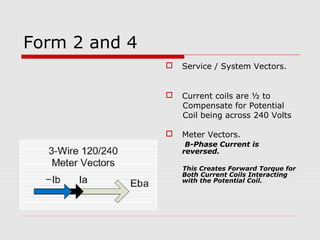
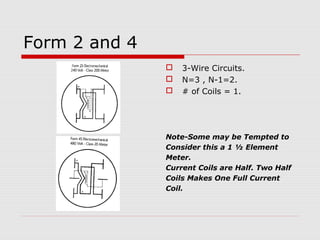
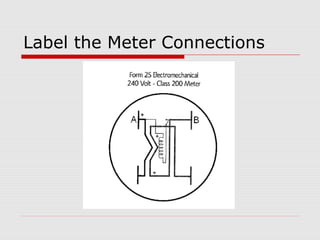
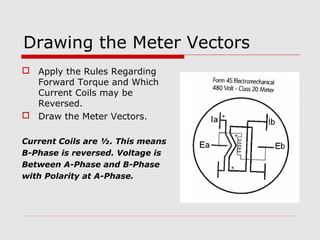
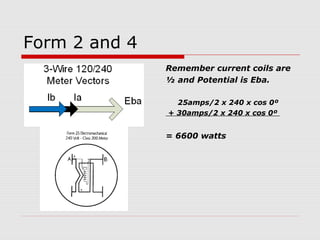
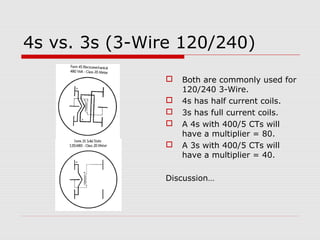
This document provides an overview of vectoring basics for electricity meters. It discusses the different meter forms, including forms 1 and 3 which have one element and conforming vectors, and forms 2 and 4 which have one element but non-conforming vectors where the B-phase current coil is reversed. The document outlines the steps for drawing meter vectors, including applying rules about forward torque and reversed current coils. It provides an example of drawing vectors for a form 2 meter with a hypothetical 3-wire load.

1. Vectoring Basics
Start With a Zero
Reference Voltage.
 Wye – ENA
 Delta – EBA

2. Vectoring Basics
 Potential – Open Arrow.
 Current – Closed Arrow.
 Arrowhead Denotes Polarity.
 A & C Currents Enter the Polarity side of a Current Coil.
 The ONLY Current Coil that is ever Reversed is B-Phase.
 B-Phase Current Coil Reverses Whenever you Alter it.
Half Coils and ‘Z’ Coils are considered altered.
 All Meter Elements Have Forward Torque at Unity Power
Factor.
You cannot have a C-Phase without first having A-Phase and
B-Phase.
Forward torque means less than 90 degrees between
the Potential coil and the current coil.

3. Sequence for Vectoring
 Learn and Memorize the Three Basic Service Vector Diagrams.
 Learn and Memorize Meter Footprints.
 The Meter Footprints show the Potential Connections and
Currents being measured. Labeling the connections is helpful.
 Apply the Rules Regarding Forward Torque and Which Current
Coils may be Reversed.
 Draw the Meter Vectors.
 Create a hypothetical load.
 Do the Math.

4. One Element Meters
 Forms 1 & 3 (Conforming)
 Forms 2 & 4 (Non-Conforming)

5. Form 1 and 3
 System Vectors.
 Meter Vectors.

6. Form 1 and 3
 Simple 2-Wire Circuit.
 N=2 , N-1=1 Element.
 Conductor w/o Current Coil
is Common to the Potential
Coil.
An Element is One
Current Coil and One
Potential Coil.

7. Form 2 and 4
 Service / System Vectors.
 Current coils are ½ to
Compensate for Potential
Coil being across 240 Volts
 Meter Vectors.
B-Phase Current is
reversed.
This Creates Forward Torque for
Both Current Coils Interacting
with the Potential Coil.

8. Form 2 and 4
 3-Wire Circuits.
 N=3 , N-1=2.
 # of Coils = 1.
Note-Some may be Tempted to
Consider this a 1 ½ Element
Meter.
Current Coils are Half. Two Half
Coils Makes One Full Current
Coil.

9. Service Vectors and Footprint

10. Label the Meter Connections

11. Drawing the Meter Vectors
 Apply the Rules Regarding
Forward Torque and Which
Current Coils may be
Reversed.
 Draw the Meter Vectors.
Current Coils are ½. This means
B-Phase is reversed. Voltage is
Between A-Phase and B-Phase
with Polarity at A-Phase.

12. Drawing the Meter Vectors
 Apply the Rules Regarding
Forward Torque and Which
Current Coils may be
Reversed.
 Draw the Meter Vectors.
Current Coils are ½. This means
B-Phase is reversed. Voltage is
Between A-Phase and B-Phase
with Polarity at A-Phase.

13. Form 2 and 4
Invent a load:
A-phase has 1200 watts.
B-phase has 1800 watts.
A-B phase has 3600 watts.
1200/120=10 amps
1800/120=15 amps
3600/240=15 amps
6600 watts total
Ia = 10+15 = 25 amps
Ib = 15+15 = 30 amps

14. Form 2 and 4
Remember current coils are
½ and Potential is Eba.
25amps/2 x 240 x cos 0º
+ 30amps/2 x 240 x cos 0º
= 6600 watts

15. 4s vs. 3s (3-Wire 120/240)
 Both are commonly used for
120/240 3-Wire.
 4s has half current coils.
 3s has full current coils.
 A 4s with 400/5 CTs will
have a multiplier = 80.
 A 3s with 400/5 CTs will
have a multiplier = 40.
Discussion…

16. The End