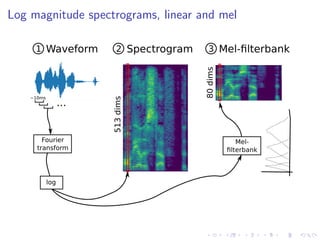
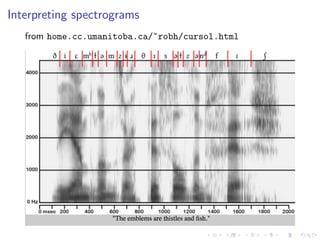
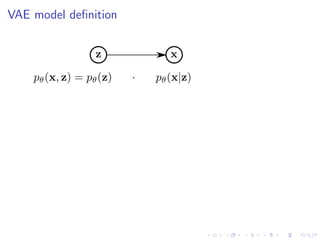
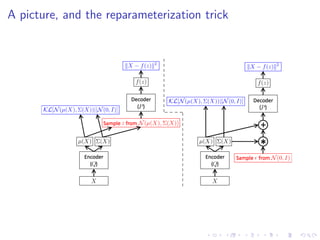
The document discusses variational autoencoders (VAEs) as a generative model for high-dimensional objects like speech and images, comparing them to autoregressive models and GANs in terms of sampling efficiency and likelihood estimation. It details the structure and challenges of VAEs, including the intractable nature of key probabilities, and explores modifications for improved latent variable representation such as β-VAEs and factor-VAEs. The document also references various studies and techniques related to disentangled representation in latent variables.

1. Variational Autoencoders for Speech
Dmytro Bielievtsov
2018

2. Log magnitude spectrograms, linear and mel

3. Interpreting spectrograms
from home.cc.umanitoba.ca/~robh/cursol.html

4. Generative models
Generative models model the distribution of high-dimensional
objects like images, audio, etc.
They model these distributions either by allowing you to
sample from the distribution or by computing likelihoods
Three families of generative model dominate the deep learning
landscape today: autoregressive, GANs, and VAEs

5. Generative model comparison
Autoregressive models can be very accurate (WaveNet) but
are slow to generate (but cf. Distilled WaveNet), and produce
no latent representation of the data
GANs produce a latent representation of the data but are
finicky to train and don’t give likelihoods (at least in their
pure form)
VAEs lack the disadvantages of autoregressive models and
GANs, but in their basic form are prone to producing blurry
samples

6. Disentangled representations
Each latent controls one “factor of variation”. You don’t have
one latent controlling, e.g., pitch + volume and another pitch
- volume
The factor of variation each latent controls is independent of
the setting of the other latents

7. VAE model definition

8. VAE model definition

9. Latent variable models, easy things to do
Drawing samples is easy: z ∼ pθ(z), x ∼ pθ(x | z)
As is computing joint likelihoods

10. Latent variable models, hard things to do
To train the model, we need to maximize pθ(x)
We also need pθ(x) if we want to find likelihoods of samples
To find latent codes of samples (e.g., to do morphing), we
need to know pθ(z | x)
Unfortunately, pθ(x) and pθ(z | x) are intractible

11. Latent variable models, intractable integrals
pθ(x) = pθ(z)pθ(x | z) dz
pθ(z | x) = pθ(z)pθ(x | z)/pθ(x)
Since z is high-dimensional, pθ(x) and pθ(z | x) are intractable
By the way, from now on we will drop θ from our notation for less
clutter

12. The idea of an encoder
For fixed x, for almost all values of z, p(z | x) will be very
nearly zero
If we could somehow train a network to approximate p(z | x),
maybe we could estimate p(x) much more efficiently by
sampling z values that are likely to generate something close
to x

13. The encoder network

14. The encoder network
Instead of using fixed variances, as with the decoder network,
the encoder network also produces variances
Intuitively, we want the network to find an efficient
representation of the data, so we penalize it for outputting
very small variances

15. The fundamental VAE equation
Start with the definition of KL-divergence and then use Bayes’ Law:
D (q(z | x) p(z | x))
= Ez∼q(z|x)[log q(z | x) − log p(z | x)]
= Ez∼q(z|x)[log q(z | x) − log p(x | z) − log p(z)] + log p(x)
Rearranging terms and using the definition of KL-divergence,
OELBO
:= log p(x) − D (q(z | x) p(z | x))
= Ez∼q(z|x)[log p(x | z)]
tractable to optimize
− D (q(z | x) p(z))
tractable to optimize

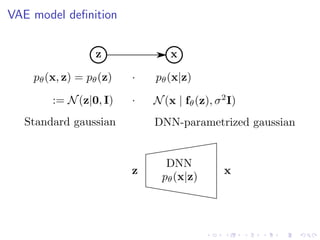
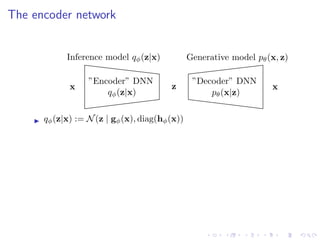
16. Recap
pθ(x | z) := N(x | fθ(z), σ2
I)
p(z) := N(z | 0, I)
qφ(z | x) := N(x | gφ(x), diag(hφ(x))
OELBO(x; θ, φ) := Ez∼qφ(z|x)[log pθ(x | z)] − D (qφ(z | x) p(z))

17. A picture, and the reparameterization trick

18. Interpretability of latent variables
Latent variables produced by vanilla VAE’s are usually meaningless
when considered individually.
Adapted from Higgins et al. 2017

19. Disentangling variables
Simple approaches to encourage disentangled latent variables:
β-VAE
factor-VAE

20. Disentangling variables: β-VAE
Original objective function (ELBO):
OELBO = Ez∼q(z|x)[log p(x | z)] − D (q(z | x) p(z))

21. Disentangling variables: β-VAE
Original objective function (ELBO):
OELBO = Ez∼q(z|x)[log p(x | z)] − D (q(z | x) p(z))
New objective function:
Oβ = Ez∼q(z|x)[log p(x | z)] − β D (q(z | x) p(z))

22. Disentangling variables: β-VAE
Adapted from Higgins et al. 2017

23. Disentangling variables: factor-VAE
Upon closer inspection, β-VAE creates some tradeoff between
disentanglement and reconstruction:
β-VAE objective:
Oβ = Ez∼q(z|x)[log p(x | z)] − β D (q(z | x) p(z))

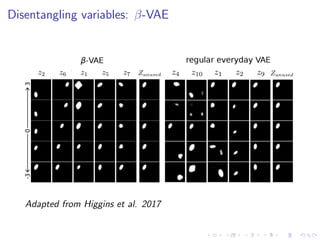
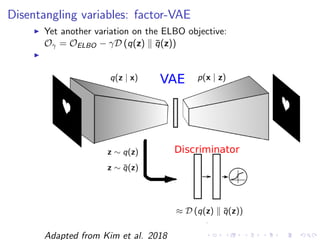
24. Disentangling variables: factor-VAE
Upon closer inspection, β-VAE creates some tradeoff between
disentanglement and reconstruction:
β-VAE objective:
Oβ = Ez∼q(z|x)[log p(x | z)] − β D (q(z | x) p(z))
Let’s look closer at that regularizer:
Ex∼pdata(x)[D (q(z | x) p(z))] = Ienc(x; z) + D (q(z) p(z))

25. Disentangling variables: factor-VAE
Upon closer inspection, β-VAE creates some tradeoff between
disentanglement and reconstruction:
β-VAE objective:
Oβ = Ez∼q(z|x)[log p(x | z)] − β D (q(z | x) p(z))
Let’s look closer at that regularizer:
Ex∼pdata(x)[D (q(z | x) p(z))] = Ienc(x; z) + D (q(z) p(z))
We don’t want to hurt that mutual information term!

26. Disentangling variables: factor-VAE
Yet another variation on the ELBO objective:
Oγ = OELBO − γD (q(z) ¯q(z))

27. Disentangling variables: factor-VAE
Yet another variation on the ELBO objective:
Oγ = OELBO − γD (q(z) ¯q(z))
Adapted from Kim et al. 2018

28. Disentangling variables: factor-VAE
Yet another variation on the ELBO objective:
Oγ = OELBO − γD (q(z) ¯q(z))
Adapted from Kim et al. 2018

29. VQ-VAE, quick look
Adapted from Oord et al. 2017

30. References
Doersch, Carl. “Tutorial on Variational Autoencoders.” ArXiv:1606.05908 [Cs, Stat], June 19, 2016.
http://arxiv.org/abs/1606.05908.
Higgins, Irina, Loic Matthey, Arka Pal, Christopher Burgess, Xavier Glorot, Matthew Botvinick, Shakir
Mohamed, and Alexander Lerchner. “β-VAE: LEARNING BASIC VISUAL CONCEPTS WITH A
CONSTRAINED VARIATIONAL FRAMEWORK,” 2017, 22.
Hsu, Wei-Ning, Yu Zhang, and James Glass. “Learning Latent Representations for Speech Generation and
Transformation.” ArXiv:1704.04222 [Cs, Stat], April 13, 2017. http://arxiv.org/abs/1704.04222.
———. “Unsupervised Learning of Disentangled and Interpretable Representations from Sequential Data.”
ArXiv:1709.07902 [Cs, Eess, Stat], September 22, 2017. http://arxiv.org/abs/1709.07902.
Kim, Hyunjik, and Andriy Mnih. “Disentangling by Factorising.” ArXiv:1802.05983 [Cs, Stat], February 16,
2018. http://arxiv.org/abs/1802.05983.
Kingma, Diederik P., and Max Welling. “Auto-Encoding Variational Bayes.” ArXiv:1312.6114 [Cs, Stat],
December 20, 2013. http://arxiv.org/abs/1312.6114.
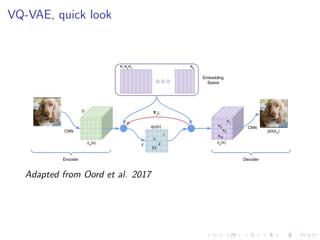
Oord, Aaron van den, Oriol Vinyals, and Koray Kavukcuoglu. “Neural Discrete Representation Learning.”
ArXiv:1711.00937 [Cs], November 2, 2017. http://arxiv.org/abs/1711.00937.