The document discusses parameter estimation for heterogeneous populations using mixed effect models, linking these models to experimental data. It presents applications to GFP transfection data and trail signaling pathways while demonstrating the development of efficient optimization methods to address challenges in estimating parameters. Additionally, it highlights the advantages of mixed effect models in computational tractability and explores various approximation and optimization techniques for parameter estimation.

1. Parameter Estimation for Heterogeneous
Populations
Fabian Fröhlich, Fabian Theis, Jan Hasenauer
Institute of Computational Biology, Helmholtz Zentrum München
and
Chair for Mathematische Modellierung biologischer Systeme, Technische Universität
München
Workshop on Numerical Methods for Optimal Control and Inverse
Problems, Garching by Munich, 11.03.2015
1 / 22

2. Outline
Description of heterogeneity via mixed effect models
Linking the mixed effect models to experimental data
Parameter estimation for mixed effect models
Application to GFP transfection data
Application to TRAIL signalling pathway
2 / 22

3. Heterogeneity in Structured Populations
Behavior of individuals:
time [h]
0 5 10 15 20
h(x)
-50
0
50
100
150
200
250
3 / 22

4. Heterogeneity in Structured Populations
Behavior of individuals:
time [h]
0 5 10 15 20
h(x)
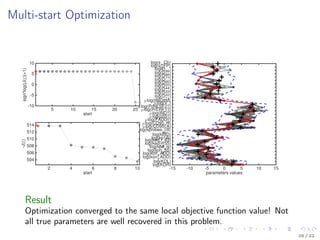
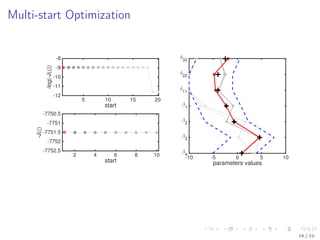
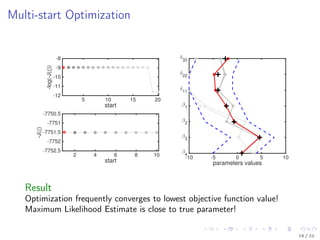
-50
0
50
100
150
200
250
Question
How can we mathematically describe this system?
3 / 22

5. Model Description
Dynamics of individual cells:
∂x
∂t
=
−ϕ1x1
ϕ3x − ϕ2x
x(t = ϕ4) =
1
0
Observation:
y(t) = x2(t)
Noise Model:
¯yij = yi (tj ) + i i ∼ N(0, σ2
i ) j = 1 . . . nt i = 1 . . . ny
4 / 22

6. Model Description
Dynamics of individual cells:
∂x
∂t
=
−ϕ1x1
ϕ3x − ϕ2x
x(t = ϕ4) =
1
0
Observation:
y(t) = x2(t)
Noise Model:
¯yij = yi (tj ) + i i ∼ N(0, σ2
i ) j = 1 . . . nt i = 1 . . . ny
Question
How to describe the system at population level?
4 / 22

7. Mixed Effect Model
Parameters of individuals consist of common effect β ∈ Rnβ
and random
effect bk
∈ Rnb k = 1 . . . ncell
ϕk
= g(β, bk
) bk
∼ N(0, D)
∂xk
∂t
= f (t, xk
; ϕk
)
xk
0 (t = w ϕk
) = v(ϕk
)
5 / 22

8. Mixed Effect Model
Parameters of individuals consist of common effect β ∈ Rnβ
and random
effect bk
∈ Rnb k = 1 . . . ncell
ϕk
= g(β, bk
) bk
∼ N(0, D)
∂xk
∂t
= f (t, xk
; ϕk
)
xk
0 (t = w ϕk
) = v(ϕk
)
Question
What are related formulations of this problem?
5 / 22

9. Related Formulations
Population Balance Equations (PBE) -> Partial Differential
Equations
Solution to ODE move along characteristics of PDE
State space (same dimension as x) is augmented by random effect
states (dimension nb)
In general linear, but high dimension of states
6 / 22

10. Related Formulations
Population Balance Equations (PBE) -> Partial Differential
Equations
Solution to ODE move along characteristics of PDE
State space (same dimension as x) is augmented by random effect
states (dimension nb)
In general linear, but high dimension of states
Advantage of Mixed Effect Model
ODE description is numerically more tractable!
6 / 22

11. Related Formulations
Population Balance Equations (PBE) -> Partial Differential
Equations
Solution to ODE move along characteristics of PDE
State space (same dimension as x) is augmented by random effect
states (dimension nb)
In general linear, but high dimension of states
Advantage of Mixed Effect Model
ODE description is numerically more tractable!
Question
How can we link our model to experimental data?
6 / 22

12. Likelihood for Mixed Effect Models
Likelihood functions are probabilisitcally motivated and link data to
models.
p(Y|β, D) =
1
γ
nk
k=1
ˆ
Rn
b
p(Yk
|bk
, β)p(bk
|D)db
Data Y = Yk
= {{¯yk
ij }
ny
i=1; tj }nt
j=1
ncell
k=1
p(Yk
|bk
, β) = exp

−
1
2
nt
j=1
ny
i=1
yk
ij − ¯yk
ij
σj
2


yk
ij = h(t, xk
; g(β, bk
))
s.t.
∂xk
∂t
= f (t, xk
; g(β, bk
))
7 / 22

13. Likelihood for Mixed Effect Models
Likelihood functions are probabilisitcally motivated and link data to
models.
p(Y|β, D) =
1
γ
nk
k=1
ˆ
Rn
b
p(Yk
|bk
, β)p(bk
|D)db
Data Y = Yk
= {{¯yk
ij }
ny
i=1; tj }nt
j=1
ncell
k=1
p(Yk
|bk
, β) = exp

−
1
2
nt
j=1
ny
i=1
yk
ij − ¯yk
ij
σj
2


yk
ij = h(t, xk
; g(β, bk
))
s.t.
∂xk
∂t
= f (t, xk
; g(β, bk
))
Question
How can we approximate the integral?
7 / 22

14. Laplace Approximation for Integral
Pinheiro [1994] suggests Laplace approximation of integral
p(Y|β, δ) ≈
ncell
k=1
ˆ
Rn
b
exp(−
1
2
Ψk (ˆbk
, β)−
1
2
(bk
−ˆbk
)T 2
bΨk (ˆbk
, β)(bk
−ˆbk
))dbk
where
Ψk (b, β, D) = −2 log p(Yk
|b, β)p(b, D)
s.t ˆbk
= arg min
b
Ψk (b, β, D) .
This approximation yields
p(Y|β, D) ≈
ncell
k=1
exp −
1
2
Ψk (ˆbk
, β) +
1
2
log (2π)nb det 2
bΨk (ˆbk
, β) .
8 / 22

15. Laplace Approximation for Integral
Pinheiro [1994] suggests Laplace approximation of integral
p(Y|β, δ) ≈
ncell
k=1
ˆ
Rn
b
exp(−
1
2
Ψk (ˆbk
, β)−
1
2
(bk
−ˆbk
)T 2
bΨk (ˆbk
, β)(bk
−ˆbk
))dbk
where
Ψk (b, β, D) = −2 log p(Yk
|b, β)p(b, D)
s.t ˆbk
= arg min
b
Ψk (b, β, D) .
This approximation yields
p(Y|β, D) ≈
ncell
k=1
exp −
1
2
Ψk (ˆbk
, β) +
1
2
log (2π)nb det 2
bΨk (ˆbk
, β) .
Question
What is the corresponding inverese problem?
8 / 22

16. Formulation as Optimization Problem
Parameter Estimation via Maximum Likelihood Estimate (MLE)
Parametric β(ξ), D(ξ)
J(ξ) = − log (p(D|β(ξ), D(ξ))) = −Ψ(ˆb, β(ξ)) +
1
2
det 2
bΨ(ˆb, β(ξ))
MLE yields hierarchical optimization problem
ˆξ = arg min
ξ
J(ξ)
where for every evaluation of J(ξ) multiple inner ODE constrained
optimisation problems have to be solved
ˆbk
= arg min
b
Ψk (b, β(ξ)) k = 1 . . . ncell
s.t.
∂x
∂t
= f (t, x; ϕ(β(ξ), b))
9 / 22

17. Properties of J(ξ)
The objective function J(ξ) in general
is non-convex
is computationally expensive to evaluate
is sufficiently smooth
Proprietary implementations [Gibiansky et al., 2012] exist but
are not extendable
do not cover all desirable features
Local gradient based methods perform well in many ODE constrained
optimization problems [Raue et al., 2013]
→ Develop an efficient local gradient based optimization schemes for
mixed effect models
10 / 22

18. Properties of J(ξ)
The objective function J(ξ) in general
is non-convex
is computationally expensive to evaluate
is sufficiently smooth
Proprietary implementations [Gibiansky et al., 2012] exist but
are not extendable
do not cover all desirable features
Local gradient based methods perform well in many ODE constrained
optimization problems [Raue et al., 2013]
→ Develop an efficient local gradient based optimization schemes for
mixed effect models
Question
How to compute gradients of J(ξ)?
10 / 22

19. Gradient of J w.r.t. ξ
Differentiation w.r.t. ξi yields
dJ
dξi
=
1
2
det 2
bΨ(ˆb, β(ξ)) Tr 2
bΨ(ˆb, β(ξ))−1 d 2
bΨ(ˆb, β(ξ))
dξi
−
1
2
dΨ
dξi
2
bΨ(b, β) is invertible at b = ˆb as the Hessian is positive definite in
isolated local minima.
For derivatives of Ψ w.r.t. ξ we need to consider the implicit dependence
of ˆb on ξ as
ˆb = arg min
b
Ψ(b, β(ξ))
11 / 22

20. Gradient of Ψ w.r.t.β
Given that ˆb is a local minimizer, we know that
bΨ(ˆb, β) = 0 .
We can then apply the implicit function theorem to obtain the local
existence of a differentiable function ˆb(β) with gradient
β
ˆb(β) = − 2
bΨ(ˆb(β), β)
−1
β bΨ(ˆb(β), β)
2
bΨ(b, β) is invertible at b = ˆb as the Hessian is positive definite in
isolated local minima.
12 / 22

21. Gradient of x w.r.t. ϕ
For
∂x
∂t
= f (t, x; ϕ)
the derivatives w.r.t. ϕi can be compute via sensitivity equations:
∂
∂t
∂x
∂ϕi
= x f (t, x; ϕ)
∂x
∂ϕi
+
∂f (t, x; ϕ)
∂ϕi
∂
∂t
∂x
∂ϕi ϕj
=
∂x
∂ϕj
T
2
x f (t, x; ϕ)
∂x
∂ϕi
+ x f (t, x; ϕ)
∂x
∂ϕi ∂ϕj
+
∂f (t, x; ϕ)
∂ϕi ∂ϕj
Efficient implementation for the computation of first order sensitivities
are available in CVODES [Serban and Hindmarsh, 2005].
13 / 22

22. Application Example 1: GFP Transfection
(Collaboration with Rädler Lab, LMU Munich)

23. Parametrization
∂xk
∂t
=
−ϕk
1x1
ϕk
3x − ϕk
2x
xk
(t = ϕk
4) =
1
0
ϕk
=




exp(β1)
exp(β2 + bk
1 )
exp(β3 + bk
2 )
exp(β4 + bk
3 )




bk
=


bk
1
bk
2
bk
3

 ∼ N




0
0
0

 ,


exp(δ11) 0 0
0 exp(δ22) 0
0 0 exp(δ33)




ξ = [ β1 β2 β3 β4 δ11 δ22 δ33 ]
15 / 22

24. Multi-start Optimization
start
5 10 15 20
-log(-J(ξ))
-12
-11
-10
-9
-8
start
2 4 6 8 10
-J(ξ)
-7752.5
-7752
-7751.5
-7751
-7750.5
parameters values
-10 -5 0 5 10
β4
β3
β2
β1
δ11
δ22
δ33
16 / 22

25. Multi-start Optimization
start
5 10 15 20
-log(-J(ξ))
-12
-11
-10
-9
-8
start
2 4 6 8 10
-J(ξ)
-7752.5
-7752
-7751.5
-7751
-7750.5
parameters values
-10 -5 0 5 10
β4
β3
β2
β1
δ11
δ22
δ33
Result
Optimization frequently converges to lowest objective function value!
Maximum Likelihood Estimate is close to true parameter!
16 / 22

26. Model-Data Comparison
time
0 5 10 15 20
h(x)
-50
0
50
100
150
200
250
data
model
time
0 5 10 15 20
residual
-30
-20
-10
0
10
20
30
40
17 / 22

27. Model-Data Comparison
time
0 5 10 15 20
h(x)
-50
0
50
100
150
200
250
data
model
time
0 5 10 15 20
residual
-30
-20
-10
0
10
20
30
40
Result
Model matches data, amplitude of residual matches standard deviation!
17 / 22

28. Application Example 2: TRAIL signalling pathway
(Collaboration with Eils Lab, DKFZ Heidelberg)

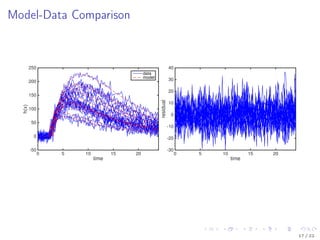
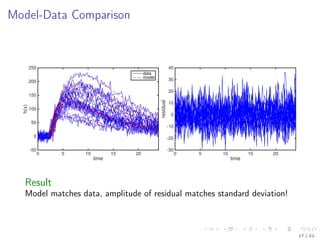
29. Model Description
Kallenberger et al. [2014] introduced a model for the TRAIL signalling
pathway.
This model was extended to account for new experimental data.
Number of parameters nϕ: 21
Number of states nx : 15
Number of observables ny : 6
Number of variable species nb: 8
19 / 22

30. Multi-start Optimization
start
5 10 15 20 25
sign*log(|J(ξ)|+1)
-10
-5
0
5
10
start
2 4 6 8 10
-J(ξ)
504
506
508
510
512
514
parameters values
-15 -10 -5 0 5 10 15
log(KDR)
log(KDL)
log(konF
ADD)
log(koffF
ADD)
log(konp
55)
log(kpdc
is)
log(kedt
rp
55)
log(kedt
rp
43)
log(kp18i)
log(kBID)
log(kprobessC
8)
µlog(CD950
A)
µlog(CD950
H)
µlog(FADD0
)
µlog(p550
)
µlog(BID0
)
µlog(PrERF10
)
µlog(PrNESF20
)
µlog(Vc
)
µlog(tBIDthd)
log(D11
)
log(D22
)
log(D33
)
log(D44
)
log(D55
)
log(D66
)
log(D77
)
log(D88
)
log(D99
)
log(sG
FP)
log(sm
Ch)
Result
Optimization converged to the same local objective function value! Not
all true parameters are well recovered in this problem.
20 / 22

31. Summary & Outlook
We developed an efficient gradient based optimization scheme
We showed that optimization works for well for low and high
dimensional problems
The method is easily extendable to account for multiple experiments
and data types
Apply developed methods to experimental data
It is possible to introduce additional penalization when the cdf of bk
and D do not match
21 / 22

32. Thanks To
Supervisors:
Fabian Theis
Jan Hasenauer
Collaboration Partners:
Joachim Rädler and Carolin Leonhardt, LMU Munich
Roland Eils and Stefan Kallenberger, DKFZ Heidelberg
Funding:
Graduate School for Quantitative Biosciences Munich
22 / 22

33. Leonid Gibiansky, Ekaterina Gibiansky, and Robert Bauer. Comparison of
Nonmem 7.2 Estimation Methods and Parallel Processing Efficiency on
a Target-Mediated Drug Disposition Model. Journal of
Pharmacokinetics and Pharmacodynamics, 39:17–35, 2012. ISSN
1567567X.
Stefan M Kallenberger, Joël Beaudouin, Juliane Claus, Carmen Fischer,
Peter K Sorger, Stefan Legewie, and Roland Eils. Intra- and
Interdimeric Caspase-8 Self-Cleavage Controls Strength and Timing of
CD95-Induced Apoptosis. Science Signaling, 7(316), 2014. ISSN
1937-9145. doi: 10.1126/scisignal.2004738.
José C Pinheiro. Topics in Mixed Effects Models. PhD thesis, 1994.
Andreas Raue, Marcel Schilling, Julie Bachmann, Andrew Matteson, Max
Schelke, Daniel Kaschek, Sabine Hug, Clemens Kreutz, Brian D
Harms, Fabian J Theis, Ursula Klingmüller, and Jens Timmer. Lessons
Learned From Quantitative Dynamical Modeling in Systems Biology.
PLoS ONE, 8(9):e74335, 2013. ISSN 1932-6203. doi:
10.1371/journal.pone.0074335.
Radu Serban and AC Hindmarsh. CVODES: An ODE Solver with
Sensitivity Analysis Capabilities. ACM Transactions on Mathematical
Software, 31(3):363–396, 2005.
22 / 22