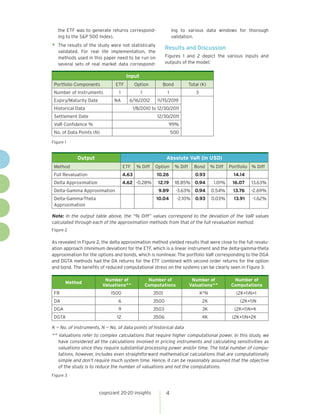
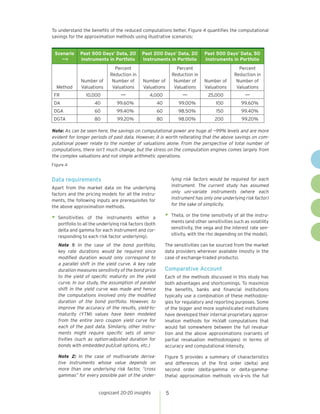
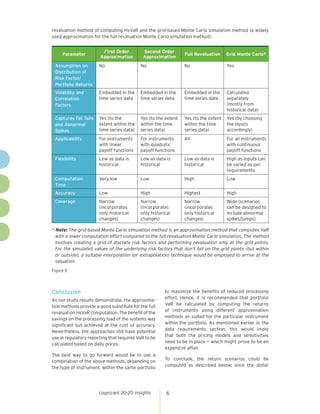
The document evaluates alternative methods to approximating historical value at risk (HsVaR) that can significantly reduce computational requirements compared to the full revaluation method, while maintaining acceptable accuracy. It considers a sample portfolio and calculates HsVaR using full revaluation and approximation methods involving delta, delta-gamma, and delta-gamma-theta. The results show the approximation methods produce HsVaR values close to full revaluation, within 1-18%, while requiring far fewer valuations, resulting in up to 99.6% reduction in computations. This demonstrates the tradeoff between accuracy and reduced processing from using approximation methods.