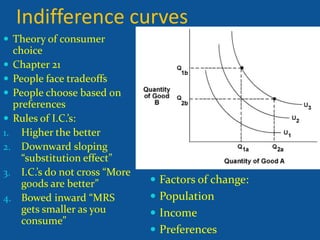
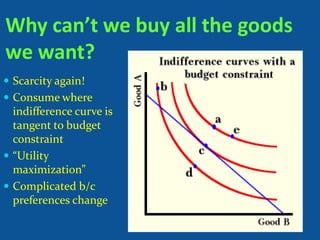
This document discusses concepts related to consumer choice and utility maximization. It provides information on: - Consumers attempting to maximize utility based on their budget constraint. - Indifference curves and how consumers choose based on preferences within the constraints of their budget. - Why consumers cannot buy all goods they want due to scarcity and must consume where their indifference curve is tangent to their budget constraint in order to maximize utility. 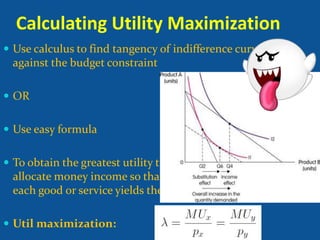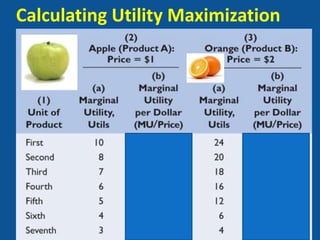- Calculating utility maximization using calculus or a formula where the marginal utility per dollar spent on each good is equal.

1. It can not be a financial asset, it much be an actual good.
Estimate price on board

2. What if Warren Buffett is
too busy to go shopping
so he gives you the cash.
 Would you still buy the one good?
 Why or why not?
 Budget constraint
 Does money always increase utility? Many goods vs. few
or one for consumers
 Ted.org video clip

3. Utility Maximization
 Consumers attempt to maximize their utility based on
their budget constraint
 Consumer surplus

4. 11/26/11
 Utility
maximization
 Pareto efficient?

5. Indifference curves
 Theory of consumer
choice
 Chapter 21
 People face tradeoffs
 People choose based on
preferences
 Rules of I.C.’s:
1. Higher the better
2. Downward sloping
“substitution effect”
3. I.C.’s do not cross “More
goods are better”
4. Bowed inward “MRS
gets smaller as you
consume”
 Factors of change:
 Population
 Income
 Preferences

6. Why can’t we buy all the goods
we want?
 Scarcity again!
 Consume where
indifference curve is
tangent to budget
constraint
 “Utility
maximization”
 Complicated b/c
preferences change

7. Calculating Utility Maximization
 Use calculus to find tangency of indifference curve
against the budget constraint
 OR
 Use easy formula
 To obtain the greatest utility the consumer should
allocate money income so that the last dollar spent on
each good or service yields the same marginal utility.
 Util maximization:

8. Assumptions:
 A consumer can buy oranges or apples
 A consumer wants $10 to spend on fruit at the farmers
market
 A consumer prefers oranges to apples
 How can this consumer maximize their utility?

9. Calculating Utility Maximization

10. Calculating Utility Maximization
Budget $420 on tickets/year
$60 per game
Games
1
2
3
4
5
6
7
Total
Utility
10
19
27
34
40
45
49
Marginal
Utility
10
9
8
7
6
5
4
Total
MU/Price Games Utility
0.166667
1
9
0.15
2
18
0.133333
3
25
0.116667
4
31
0.1
5
36
0.083333
6
40
0.066667
7
44
$60 per game
Marginal
Utility
9
9
7
6
5
4
4
MU/Price
0.15
0.15
0.116667
0.1
0.083333
0.066667
0.066667

12. Calculating Profit Maximization

13. Calculating Profit Maximization

15. Mankiw
 Pages 464-465
 #15 then #12
 EC #14