CLASS 9 TRIANGLE

1. CLASS – XTH
TOPIC - TRINAGLES
Name:- Sandeep Jaiswal
11813483
Integrated B.Sc. B.Ed.

2. A
B C
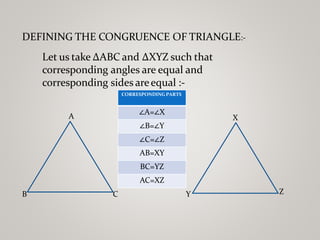
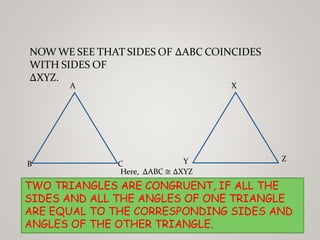
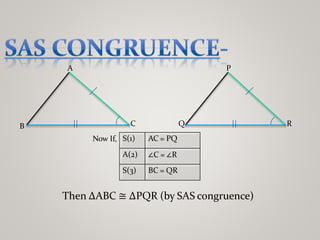
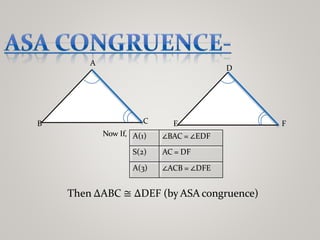
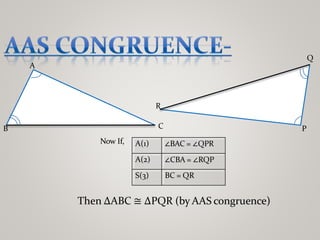
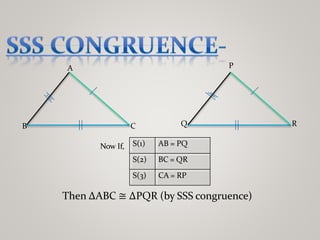
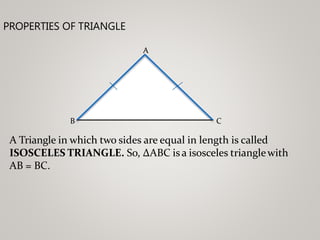
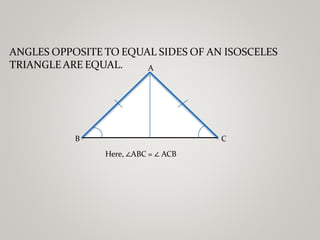
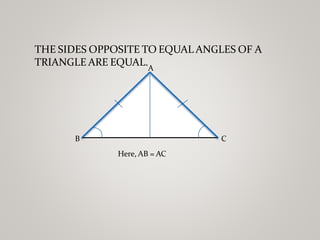
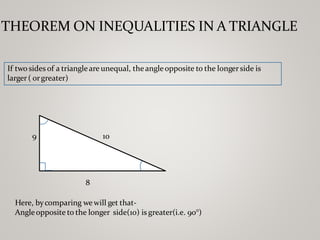
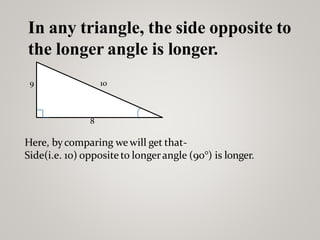
We know that a closed figure formed by three intersecting lines is called a
triangle(‘Tri’ means ‘three’).
A triangle has three sides, three angles and three vertices.
For e.g.-in
TriangleABC, denoted as ∆ABC AB,BC,CAare the three sides, ∠A,∠B,∠C are
three angles and A,B,C are three vertices.

3. DEFINING THE CONGRUENCE OF TRIANGLE:-
Let us take ∆ABC and ∆XYZ such that
corresponding angles are equal and
corresponding sides areequal :-
A
B C
X
Y Z
CORRESPONDING PARTS
∠A=∠X
∠B=∠Y
∠C=∠Z
AB=XY
BC=YZ
AC=XZ

4. NOW WE SEE THAT SIDES OF ∆ABC COINCIDES
WITH SIDES OF
∆XYZ.
B C
A X
Y Z
SO WE GET THAT
TWO TRIANGLES ARE CONGRUENT, IF ALL THE
SIDES AND ALL THE ANGLES OF ONE TRIANGLE
ARE EQUAL TO THE CORRESPONDING SIDES AND
ANGLES OF THE OTHER TRIANGLE.
Here, ∆ABC ≅ ∆XYZ

5. THISALSO MEANS
THAT:- A corresponds to X
B corresponds to Y
C corresponds to Z
Forany twocongruent triangles the corresponding
parts areequal and are termed as:-
CPCT – Corresponding Parts of Congruent Triangles

6. CRITERIAS FOR CONGRUENCE OF TWO TRIANGLES
SAS(side-angle-side) congruence
• Twotrianglesarecongruent if twosidesand the included angleof one triangleare
equal to the twosidesand the included angleof othertriangle.
ASA(angle-side-angle) congruence
• Twotrianglesarecongruent if twoanglesand the included sideof one triangleare
equal to twoanglesand the included sideof othertriangle.
AAS(angle-angle-side) congruence
• Twotrianglesarecongruent if any two pairs of angleand one pairof corresponding
sidesareequal.
SSS(side-side-side) congruence
• If three sidesof one triangleareequal to the three sidesof another triangle, then the
two trianglesarecongruent.
RHS(right angle-hypotenuse-side) congruence
• If in two right-angled triangles the hypotenuseand onesideof one triangleareequal to
the hypotenuseand onesideof theother triangle, then the two trianglesarecongruent.

7. A
B C
P
Q R
S(1) AC = PQ
A(2) ∠C = ∠R
S(3) BC = QR
Now If,
Then ∆ABC ≅ ∆PQR (by SAS congruence)

8. A
B C
D
E F
Now If, A(1) ∠BAC = ∠EDF
S(2) AC = DF
A(3) ∠ACB = ∠DFE
Then ∆ABC ≅ ∆DEF (by ASA congruence)

9. A
B C P
Q
R
Now If, A(1) ∠BAC = ∠QPR
A(2) ∠CBA = ∠RQP
S(3) BC = QR
Then ∆ABC ≅ ∆PQR (by AAS congruence)

10. Now If, S(1) AB = PQ
S(2) BC = QR
S(3) CA = RP
A
B C
P
Q R
Then ∆ABC ≅ ∆PQR (by SSS congruence)

11. Now If, R(1) ∠ABC = ∠DEF = 90°
H(2) AC = DF
S(3) BC = EF
A
B C
D
E F
Then ∆ABC ≅ ∆DEF (by RHS congruence)

12. PROPERTIES OF TRIANGLE
A
B C
A Triangle in which two sides are equal in length is called
ISOSCELES TRIANGLE. So, ∆ABC isa isosceles trianglewith
AB = BC.

13. ANGLES OPPOSITE TO EQUAL SIDES OF AN ISOSCELES
TRIANGLE ARE EQUAL.
B C
A
Here, ∠ABC = ∠ ACB

14. THE SIDES OPPOSITE TO EQUAL ANGLES OF A
TRIANGLE ARE EQUAL.
C
B
A
Here, AB = AC

15. THEOREM ON INEQUALITIES IN A TRIANGLE
If two sides of a triangleare unequal, theangleopposite to the longer side is
larger( orgreater)
10
9
8
Here, bycomparing wewill get that-
Angleopposite to the longer side(10) is greater(i.e. 90°)

16. 10
9
8
Here, bycomparing we will get that-
Side(i.e. 10) opposite to longerangle (90°) is longer.
In any triangle, the side opposite to
the longer angle is longer.

17. 10
9
8
Here bycomparing weget-
9+8>10
8+10>9
10+9>8
So, sum of any two sides isgreater than the third side.
The sum of any two side of a triangle is
greater than the third side.