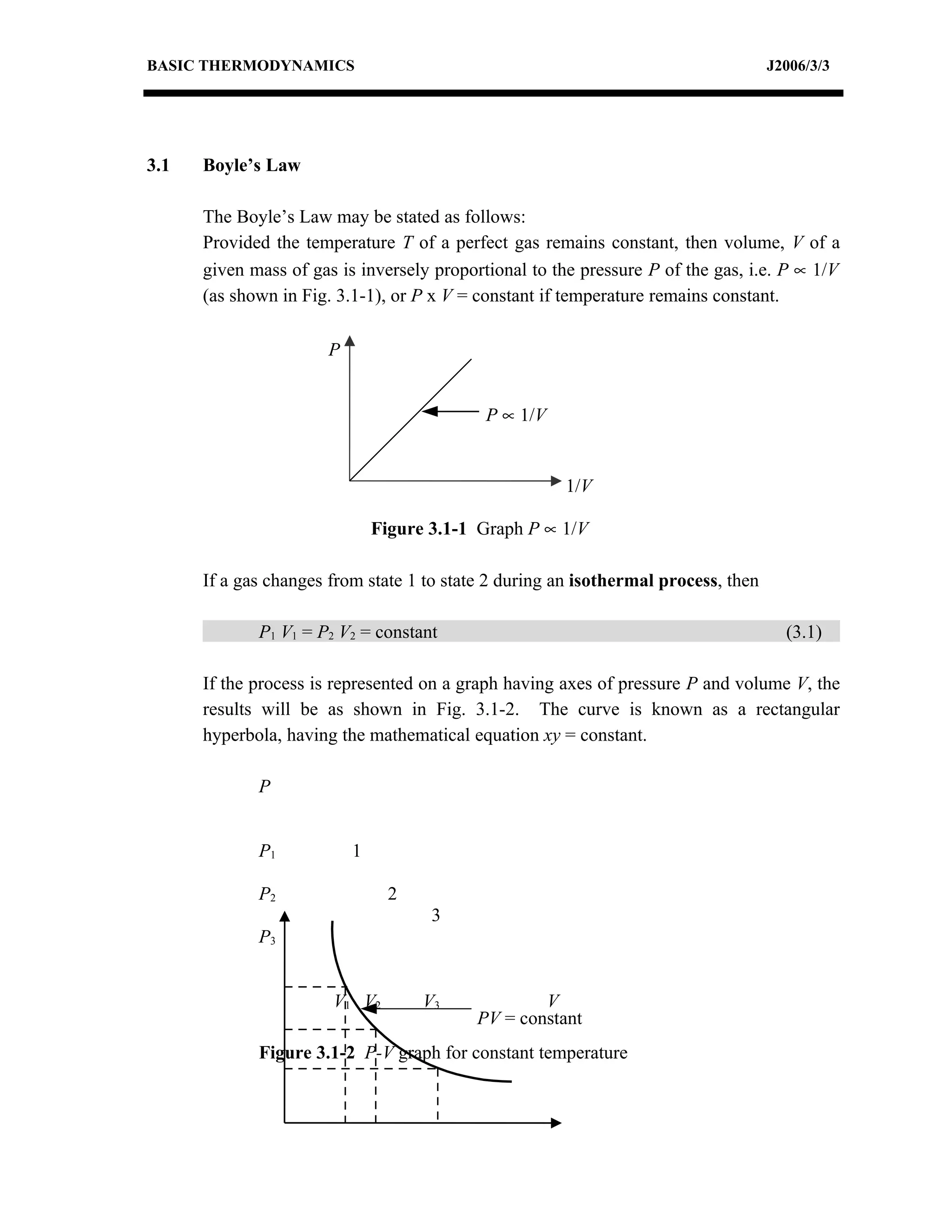
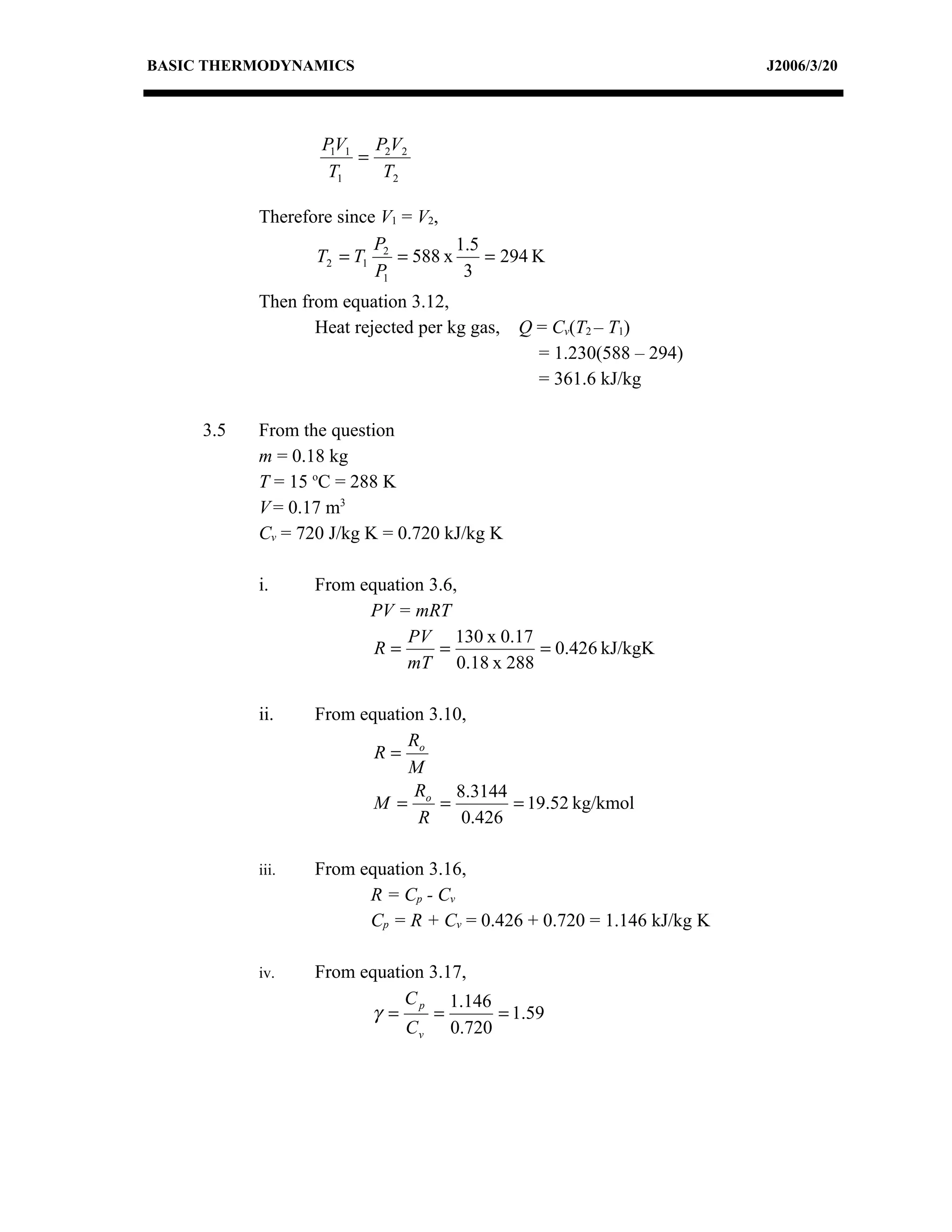
This document discusses basic thermodynamics concepts. It begins by defining a perfect gas and stating Boyle's Law and Charles' Law, which describe the relationships between pressure, volume, and temperature in gases. It then defines specific heat capacity at constant volume (Cv) as the amount of heat required to raise the temperature of a gas by 1 degree Celsius while keeping its volume constant. The document provides equations relating heat transfer, temperature change, and internal energy for a constant volume process involving a perfect gas. It explains that for such a process, no work is done since the piston cannot move during constant volume heating or cooling.