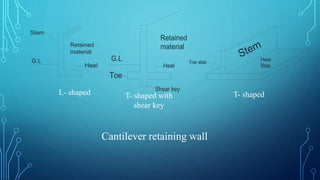
The document presents a comprehensive guide on the design of cantilever retaining walls, focusing on the specifications and calculations required for such structures, including stability checks and component design. It includes detailed calculations for earth pressure, dimensions, and stability factors based on given parameters, along with material specifications and reinforcement details. The design follows the requirements for a retaining wall with height specifications, ensuring safety against sliding and overturning forces.

1. A. D. PATEL INSTITUTE OF TECHNOLOGY
Civil Engineering Department
Topic:-Cantilever Retaining Wall
Design of Reinforced Concrete Structures
Guide By :
Prof. Darshan Yagnik
Prof. Tausif Kauswala
Academic Year 2020-21
Present By :
Harsh Shani

2. CANTILEVER RETAINING WALL
This is a most common type of retaining wall. It is consists of a vertical wall (stem),
heel slab and toe slab which act as cantilever beams. Its stability is maintained by the weight of
the retaining wall and the weight of the earth on the heel slab of the retaining wall. It is
generally used when the height of wall up to 6m.
The cantilever retaining wall resists the horizontal earth pressure as wall as other
vertical pressure by way bending of various components acting as cantilevers.

3. Heel
Stem
G.L
Retained
material
Cantilever retaining wall
Heel
Shear key
Toe
Retained
material
G.L Toe slab
Stem
Heel
Slab
T- shaped with
shear key
T- shaped
L- shaped

4. EXAMPLE
Design a cantilever retaining wall to retain the earth of height 5.5 m
above the ground level. Fix the dimensions and carry out stability checks of
retaining wall . Design all component and Provide all necessary checks.
Take SBC of soil = 175 kN/𝑚2
∅ = 30º , µ = 0.5
Unit weight of soil = 18 kN/𝑚3
Use M20 grade of concrete and Fe 415 grade of steel.

5. Solution :-
1. Coefficients of earth pressure :-
∅ = 30º
𝐾𝑎=
1−sin ∅
1+sin ∅
=
1−sin 30
1+sin 30
=
1
3
∴ 𝐾𝑝 =
1
𝐾𝑎
= 3

6. 2. Preliminary dimensions :
𝛾 =18 kn/𝑚3
SBC of soil = 175 kn/𝑚2
∴ the minimum depth of foundation is
𝑑𝑚𝑖𝑛=
𝑞0
𝛾
1−sin ∅
1+sin ∅
2
=
175
18
1
3
2
= 1.08 m
∴ provide depth of foundation as 1.2 m
∴ overall depth of retaining wall ,
H = 5.5 +1.20
H = 6.70 m

7. H/3
𝑃𝑎
5.5m
1.2 m
h
H
𝑃𝑎=𝐾𝑎*𝛾 ∗ H
Active earth pressure diagram
b

8. • Base width (b)
For ‘T’ shaped retaining wall, the minimum base width may be taken as :
b =
3𝑃
2 𝛾
P = ½*𝐾𝑎*𝛾*ℎ2
=
1
2
*
1
3
*18*6.702 = 134.67 kN
∴ b =
3 𝑥 134.67
2 𝑥 18
= 3.35m
Consider toe width =
1
3
x b =
1
3
x 3.35 =1.12m
∴ Provide toe width = 1.2m
∴ Provide total base width = 4.0m

9. • Thickness of base slab :
Thickness =
𝐻
12
to
𝐻
15
=
6.7
12
to
6.7
15
= 0.558 to 0.446m
consider uniform thickness of base slab = 0.5m
• Thickness of stem at base :
Pressure at the base of stem
𝑃𝑎=𝐾𝑎*𝛾 ∗ h
h = 6.70 – 0.50 = 6.20 m

10. ∴ maximum moment at the base of stem
=
1
2
𝐾𝑎∗𝛾 ∗ ℎ2
x
ℎ
3
=
1
2
∗
1
3
∗ 18 ∗
6.203
3
= 238.32 kNm
factored moment = 1.5 * 238.32
Mu= 357.48 kNm
For Fe 415 steel,
Mu = 0.138*fck*b*𝑑2
357.48*106= 0.138*20*1000*𝑑2
d = 359.89 mm
SP.16
Page no .10

11. Consider 50 mm effective cover
∴ total d for stem required = 359.89 + 50
= 409.89 mm
Provide total depth of stem = 450 mm
∴ Width of heel = 4.00-1.20-0.45 =2.35m
Provide top width of stem = 0.20m
Provide shear key of size 0.45m x 0.50m below base to prevent sliding of the wall

12. 3. Stability calculations :
H/3
𝑃𝑎
5.5m
1.2 m
h=6.20m
H=6.70m
𝑃𝑎=𝐾𝑎*𝛾 ∗ H = 40.2 kN/𝑚2
Active earth pressure diagram
b = 4m
0.25 0.2
0.2
0.7m
0.5m
Toe
0.5m
1.20 m 0.45 m 2.35m
𝑊1
𝑊2
𝑊3
𝑊4
𝑊5
G.L.
Back fill
Heel
Shear key
stem
A B
C D

13. The over all dimensions of the retaining wall are shown in fig
Consider 1m length of wall
Horizontal active pressure at the base of the wall
= 𝐾𝑎*𝛾 ∗ h = 1
3
∗ 18 ∗6.7 = 40.2 kN/𝑚2
• Horizontal loads :
Sliding force , 𝑃𝑎ℎ = 134.67 kN ←
Overturning moment, 𝑀𝑜 = 300.31 kNm ↺
Load type Horizontal load (kN) Perpendicular
distance for A (m)
Moment about A
(kNm)
Active earth
pressure
1
2
∗ 40.2 ∗6.7 = 134.67 kN
6.7
3
=2.23m 300.31 kNm
Total 𝑃𝑎ℎ = 134.67 kN ← 𝑀𝑜 = 300.31 kNm↺

14. • Vertical loads :
density of concrete = 25 kn/𝑚3
density of soil = 18 kn/𝑚3
Sr
no
Load type Horizontal load (kN) Perpendicular distance
for A (m)
Moment
about A
(kNm)
1 Stem -𝑊1 𝑊1= (6.20*0.20)*25=31kN 1.2+0.25+0.1=1.55m 48.05
2 Stem − 𝑊2 𝑊2= (
1
2
*0.25*6.2)*25 = 19.375kN 1.2+
2
3
*0.25 = 1.37 m 26.54
3 Base slab- 𝑊3 𝑊3= (4*0.5)*25 = 50kN 4
2
= 2m 100.00
4 Shear key - 𝑊4 𝑊4= (0.45*0.5)*25 =5.625 kN 1.2+
0.45
2
= 1.425 m 8.02
5 Backfill - 𝑊5 𝑊5= (2.35*6.2)*18 = 262.26 kN 1.2+0.45+
2.35
2
= 2.825m 740.88
Total 𝑊 = 368.26 kN ↓ 𝑀𝑟 = 923.49
kNm ↻

15. ∴ Total downward load, 𝑊 = 368.26 kN ↓
Resisting moment , 𝑀𝑟 = 923.49 kNm ↻
Let, distance of C.G. of vertical loads from the face of the toe, i.e. from point A is x .
𝑊 *x = net moment at A (toe)
∴ x =
(923.49−300.31)
368.26
= 1.69m
Hence, eccentricity e =
𝑏
2
- x
=
4
2
- 1.69
= 0.31 m
𝑊
𝑏
2
x e

16. • Maximum pressure at A (toe) :
𝑃𝑚𝑎𝑥=
𝑤
𝑏
1 +
6𝑒
𝑏
=
368.26
4
1 +
6∗0.31
4
= 134.86 kN/𝑚2 ……..at toe
• Minimum pressure at B (Heel) :
𝑃𝑚𝑖𝑛=
𝑤
𝑏
1 −
6𝑒
𝑏
=
368.26
4
1 −
6∗0.31
4
= 49.25 kN/𝑚2 ……..at heel
𝑃𝑚𝑎𝑥 = 134.86 kN/𝑚2
< 175 kN/𝑚2
……safe
𝑃𝑚𝑖𝑛 = 49.2 kN/𝑚2
> 0 i.e. not negative.
Therefore, no tension at base .

17. • Factor of safety against overturning :
Resisting moment , 𝑀𝑟 = 923.49 kNm ↻
Overturning moment, 𝑀𝑜 = 300.31 kNm ↺
∴ F.S. =
𝑀𝑟
𝑀𝑜
=
923.49
300.31
= 3.07>1.55 ………. Safe
• Factor of safety against sliding :
Sliding force , 𝑃𝑎ℎ = 134.67 kN ←
Frictional force =𝜇 ∗ 𝑊
= 0.5*368.26
=184.13 kN → 0.5m
0.5m
𝜇 ∗ 𝑊
0.7 m
ℎ1 = 1m
𝑊
𝐾𝑎*𝛾 ∗ ℎ1
=3*18*1.0
=54 kN/𝑚2

18. Passive pressure under the base of Key
𝑃𝑝= 𝐾𝑎*𝛾 ∗ ℎ1
=3*18*1.0
=54 kN/𝑚2
total 𝑃𝑝 =
1
2
* 54 *1.0
= 27 kN →
total restoring force
= 𝜇 ∗ 𝑊 + 𝑃𝑝
= 184.13+27
=211.13 kN →
F.S. =
𝑟𝑒𝑠𝑡𝑜𝑟𝑖𝑛𝑔 𝑓𝑜𝑟𝑐𝑒
𝑠𝑙𝑖𝑑𝑖𝑛𝑔 𝑓𝑜𝑟𝑐𝑒
=
211.13
134.67
= 1.57 > 1.55 …….safe
ℎ1 = 0.5 +0.5
= 1.0m

19. 4. Design of stem :
Stem acts as a cantilever of height 6.20 m
Subjected to uniformly varying load of = 𝐾𝑎*𝛾*h
=
1
3
* 18*6.2
= 37.2 kN/𝑚2
∴ B.M. at the base of stem =
1
2
*(37.2*6.2) *
1
3
*6.2
= 238.32 kNm
∴ factored moment, Mu = 1.5*238.32
= 357.48 kNm
𝐴𝑠𝑡 required ,
𝑀𝑢
𝑏𝑑2 =
357.48
1000∗(400)2
𝑀𝑢 = 2.23
SP.16
Page no : 48
d = 450-50
=400mm

20. ∴ 𝑝𝑡 = 0.730 %
∴ 𝐴𝑠𝑡 =
𝑝𝑡
100
*bd
=
0.730
100
*1000*400
= 2920 𝑚𝑚2
∴ Provide 20mm ∅ bars @ 100 mm c/c (𝐴𝑠𝑡 = 3142 𝑚𝑚2
)
• Distribution steel :
Average thickness of stem =
200+450
2
= 325𝑚𝑚
Provide minimum 0.12 % steel as distribution steel
∴ 𝐴𝑠𝑡 =
𝑝𝑡
100
*bd
=
0.12
100
*1000*350
= 390 𝑚𝑚2
Provide 10mm ∅ bars @ 200 mm c/c (𝐴𝑠𝑡 = 390 𝑚𝑚2) on tension face (in horizontal direction)

21. On the outer face use 0.06% steel both ways.
∴ Provide 10mm ∅ bars @ 300 mm c/c both ways on the outer face.
• Curtailment of vertical bars :
Bending moment at depth h from top of wall
M =
1
2
𝐾𝑎∗𝛾 ∗ ℎ2 x
ℎ
3
=
1
6
𝐾𝑎∗𝛾 ∗ ℎ3
∴ bending moment I proportional to ℎ3
.
𝐴𝑠𝑡 required is proportional to B.M. / effective depth.
∴ 𝐴𝑠𝑡 ∝
ℎ3
𝑑
∴
𝐴𝑠𝑡1
𝐴𝑠𝑡
=
ℎ1
3 /𝑑1
ℎ3/𝑑
∴
𝐴𝑠𝑡1
𝐴𝑠𝑡
=
ℎ1
3 ∗𝑑
ℎ3∗𝑑1

22. 𝑑1 = 𝑑𝑡+
(𝑑−𝑑𝑡)
ℎ
∗ ℎ1
= 150+
(450−150)
6200
∗ ℎ1
= 150+0.04ℎ1
For 50 % curtailment of steel ,
𝐴𝑠𝑡1
𝐴𝑠𝑡
=
1
2
∴
𝐴𝑠𝑡1
𝐴𝑠𝑡
=
ℎ1
3 ∗𝑑
ℎ3∗𝑑1
∴
1
2
=
ℎ1
3 ∗400
62003∗150+0.04ℎ1
∴ 1.787x1013
+ 4.766x109
ℎ1 = 400ℎ1
3
Solving by calculator from 3-degree,
ℎ1 = 4642.11
= 4.64 m from top of wall.
𝑑𝑡= 200-50
= 150 mm
d = 450-50
= 400 mm

23. Theoretical cut off point from bottom of stem
= 6.20-4.64
=1.56 m
The bars should extend a development length from the theoretical cut off point.
For M20 , Fe 415
𝐿𝑑 = 47 ∅
= 47*20 = 940mm
∴ Actual cut off point from bottom of stem, = 1.56+0.94
= 2.50 m
∴ curtail 50% of bars at 2.5 m from bottom of stem.
Similarly curtail 50% of remaining bars at 4.5m from bottom of stem.

24. • Check for shear :
Pressure at base of stem =𝐾𝑎*𝛾*h
=
1
3
* 18*6.2
= 37.2 kN/𝑚2
Shear at base of stem = V =
1
2
*37.2*6.2 = 115.32kN
∴ Vu = 1.5*115.32 = 172.98 kN
∴ 𝜏𝑣 =
𝑉𝑢
𝑏𝑑
=
172.98∗103
1000∗400
= 0.432𝑁/𝑚𝑚2
∴ 𝑝𝑡 =
𝐴𝑠𝑡 ∗100
𝑏𝑑
=
100∗3142
1000∗400
= 0.785%
𝜏𝑐 = 0.57 𝑁/𝑚𝑚2
> 0.432𝑁/𝑚𝑚2
….safe
IS:456-2000
Page no .72,73

25. 5. Design of Heel Slab :
Pressure Distribution below base
1.20 0.45 2.35
A B C D
134.86 kN/m2
49.25 kN/m2
p=109.18 kN/m2
p=99.54 kN/m2
49.25
86.61

26. Pressure at the junction of stem with heel slab is
4 m → 85.61 (difference)
2.35 m → ? (50.29)
∴p = 49.25 + 50.29
= 99.54 kN/m2 (at D)
Pressure at the junction of stem with toe slab is
4 m → 85.61 (difference)
2.80 m → ? (59.93)
∴ p = 49.25 + 59.93
= 109.18 kN/m2
width of heel slab is 2.35 m

27. Total downward pressure on heel slab
= weight of backfill + self weight of heel slab
= (6.2 x 18) + (0.5 x 25)
= 124.10 kN/m2 ↓
2.35 m
99.54 kN/m2
49.25 kN/m2
124.10 kN/m2 124.10 kN/m2
24.56 kN/m2
24.56kN/m2
50.29kN/m2
74.56 kN/m2
2.35 m
Upward Pressure Downward Pressure Net Pressure
NET PRESSURES ON HEEL

28. Maximum S.F. at D = (24.56 x 2.35) + (2x 2.35 x 50.29)
= 57.72 + 59.10 = 116.82 kN
Factored S.F.
Vu= 1.5 x 116.82
= 175.23 kN
Maximum B.M. at D = 57.72 ∗
2.35
2
+ 59.10 ∗
2
3
∗ 2.35
= 67.82 + 92.59
= 160.41 kNm
Factored B.M.,
Mu = 1.5 x 160.41
= 240.62 kNm
d = 500 — 50 = 450 mm

29. 𝑀𝑢
𝑏𝑑2 =
240.62∗106
1000∗4502
= 1.188
∴ 𝑝𝑡 = 0.355%
W
P
Tension face
Tension face
Tension face
x x
z
Soil pressure
DEFORMATION CHARACTERISTICS OF RETAINING WALL

30. ∴ 𝐴𝑠𝑡 =
𝑝𝑡
100
*bd
=
0.355
100
*1000*450
= 1597.50 𝑚𝑚2
Provide 16 mm @ 120 mm c/c (𝐴𝑠𝑡 =1675 mm2) on top face of heel
• Check for shear :
∴ 𝜏𝑣 =
𝑉𝑢
𝑏𝑑
=
175.23∗103
1000∗450
= 0.389𝑁/𝑚𝑚2
∴ 𝑝𝑡 =
𝐴𝑠𝑡 ∗100
𝑏𝑑
=
100∗1675
1000∗450
= 0.372%
From IS : 456-2000, Table - 19, Page 73
𝜏𝑐 = 0.418 𝑁/𝑚𝑚2
> 0.389 𝑁/𝑚𝑚2
….safe

31. • Distribution Steel :
Provide minimum 0.12% steel of gross cross sectional area
∴ 𝐴𝑠𝑡 =
𝑝𝑡
100
*bd
=
0.12
100
*1000*500
= 600 𝑚𝑚2
Provide 10mm ∅ bars @ 130 mm c/c (𝐴𝑠𝑡 = 604 𝑚𝑚2
)
Also provide 10 0 @ 260 mm c/c both ways on bottom face for crack control.
• Anchorage Length :
Anchorage length required = 𝐿𝑑
= 47 ∅
= 47 x 16
= 752 mm = 800 ram
extend the main steel of heel for a length 800 mm from D to the left side
IS :456-2000
Page no : 48
from Sp. 16, P. 184

32. 6. Design of toe slab :
Toe slab is designed as a cantilever slab.
Total downward pressure on toe
= Self weight of toe slab
= 0.5 x 25
= 12.5 kN/m2
134.86 kN/m2
109.18 kN/m2
12.5 kN/m2 12.5 kN/m2
122.36 kN/m2
96.68 kN/m2
1.20 m
25.68
Upward Pressure Downward Pressure Net Pressure
1.20 m
A C
A C
C
A
Net pressures on toe
Critical section

33. Maximum B.M. at C
= 1.20 ∗ 96.68 ∗
1.20
2
+
1
2
∗ 1.20 ∗ 25.68 ∗
2
3
∗ 1.20
= 69.61 + 12.32 = 81.93 kNm
Factored B.M.,
Mu= 1.5 x 81.93 = 122.90 kNm
𝑀𝑢
𝑏𝑑2 =
122.90∗106
1000∗4502
= 0.61
∴ 𝑝𝑡 = 0.175%
∴ 𝐴𝑠𝑡 =
𝑝𝑡
100
*bd
=
0.175
100
*1000*450
= 787.5 𝑚𝑚2

34. Half the reinforcement of stem i.e. 20 ∅ @ 200 mm c/c =
3142
2
= 1571 mm2 anchored in toe
will serve as toe reinforcement.
• Distribution Steel :
Provide minimum 0.12% steel of gross cross sectional area
∴ 𝐴𝑠𝑡 =
𝑝𝑡
100
*bd
=
0.12
100
*1000*500
= 600 𝑚𝑚2
Provide 10mm ∅ bars @ 130 mm c/c (𝐴𝑠𝑡 = 604 𝑚𝑚2)

35. 7. Design of shear key :
Size of shear key provided is 0.45 m x 0.50 m
Provide minimum reinforcement in key
∴ 𝐴𝑠𝑡 =
𝑝𝑡
100
*bd
=
0.12
100
*1000*450
= 540 𝑚𝑚2
Half the main reinforcement of stem are anchored in key =
3142
2
= 1571𝑚𝑚2
Also extend temperature reinforcement of stem on outer face in the shear key. This is 10 ∅ @
400 mm c/c = 196 nun2
Total 𝐴𝑠𝑡 in key = 1571 + 196
= 1767 mm2 > 540 mm2 …….ok

36. 20 ∅ @ 400 mm c/c
10 ∅ @ 200 mm c/c
20 ∅ @ 200 mm c/c
10 ∅ @ 130 mm c/c
16 ∅ @ 120 mm c/c
20 ∅ @ 200 mm c/c
10 ∅ @ 130 mm c/c
10 ∅ @ 130 mm c/c
both way
10 ∅ @ 260 mm c/c
both way
20 ∅ @ 100 mm c/c
Stem reinforcement
Cross section