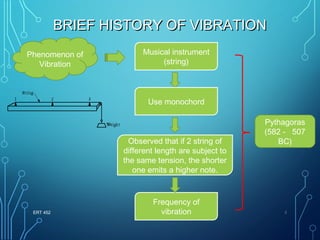
This document provides an overview of vibrations, including: 1) A brief history of vibration studies from Pythagoras to modern scientists like Galileo and Newton. Frahm later proposed using dynamic vibration absorbers to eliminate unwanted vibrations. 2) It discusses the importance of studying vibrations to reduce failures in machines and structures, and explores applications in manufacturing and other fields. 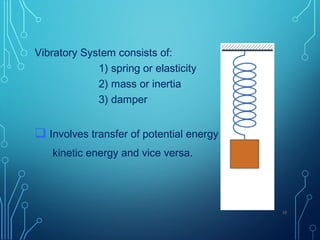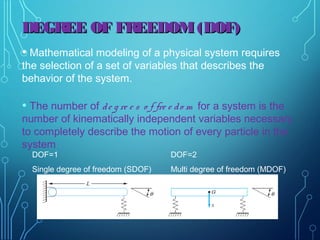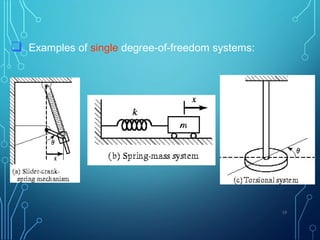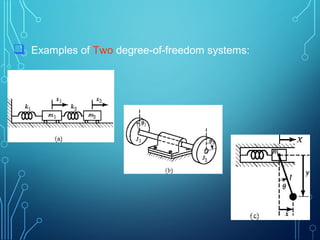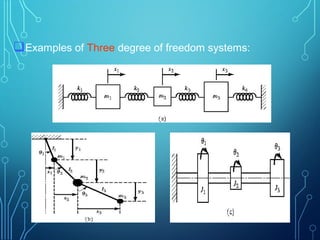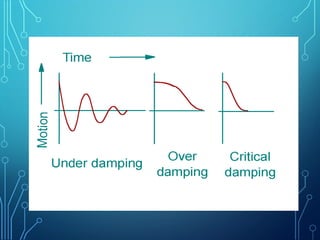3) Basic concepts of vibrations are introduced like period, frequency, resonance, and the three main types of vibration: longitudinal, transverse, and torsional. Classifications of free and forced vibrations as well as degrees of freedom in systems are also covered.

1. VIBRATIONS
SATYENDRA KUMARSANTSATYENDRA KUMARSANT
1630071308516300713085
66THTH
SEM[ JAN- JUNE 2016]SEM[ JAN- JUNE 2016]
1

2. TOPIC OUTLINE
Introduction – History and Importance of Vibrations
Importance of the Study of Vibration
 Basic Concepts of Vibrations
 Classification of Vibration
Damping
Sources
2

3. BRIEF HISTORY OF VIBRATIONBRIEF HISTORY OF VIBRATION
ERT 452 3
Phenomenon of
Vibration
Musical instrument
(string)
Observed that if 2 string of
different length are subject to
the same tension, the shorter
one emits a higher note.
Use monochord
Frequency of
vibration
Pythagoras
(582 - 507
BC)

4. (1564 – 1642) Galileo Galilei
- Founder of modern experimental science.
- Started experimenting on simple pendulum.
- Study the behavior of a simple pendulum
(observe pendulum movement of a lamp).
- Describing resonance, frequency, length,
tension and density of a vibrating stretched
string.
4
(1642 – 1727) Sir Isaac Newton
- Derive the equation of motion of a
vibrating body.

5. (1902 – 1909) Frahm
- Investigate the importance of torsional
vibration study in the design of the
propeller shafts of steamships.
- Propose the dynamic vibration absorber,
which involves the addition of a
secondary spring-mass system to
eliminate the vibration of main system.
5

6. More often, vibration is undesirable, wasting energy
and creating unwanted sound – noise!
The vibrational motions of
engines, electric motors,
other mechanical devices
which are usually the results
of imbalance in rotating
parts, uneven friction,
meshing gear, etc. are
typically unwanted!

7. IMPORTANCE OF THE STUDY OFIMPORTANCE OF THE STUDY OF
VIBRATIONVIBRATION
Vibrations can lead to excessive deflections and
failure on the machines and structures.
To reduce vibration through proper design of
machines and their mountings.
To utilize profitably in several consumer and
industrial applications.
To improve the efficiency of certain machining,
casting, forging & welding processes.
To stimulate earthquakes for geological research
and conduct studies in design of nuclear reactors.
7

8. BASICBASIC
CONCEPTS OFCONCEPTS OF
VIBRATIONVIBRATION
ERT 452 8

9. WHAT İS VİBRATİON ?
• Vibration is defined as mechanical oscillations of a
system about an equilbrium position.

10. Vibratory System consists of:
1) spring or elasticity
2) mass or inertia
3) damper
 Involves transfer of potential energy to
kinetic energy and vice versa.
10

11. PERIOD – It is the time taken by the motion to
repeat itself, and is measured in Seconds.
CYCLE – It is the Motion completed during one
time period.
FREQUENCY – Number of cycles of motion
completed in one second. Expressed in Hz (Hertz)
RESONANCE - When the frequency of the
external force is the same as that of the natural
frequency of the system, a state of resonance is
said to have been reached. Resonance results in
large amplitude of vibrations and this may be
dangerous. 11

12. TYPES OF VIBRATIONSTYPES OF VIBRATIONS
LONGITUDINAL VIBRATIONS
A continuing periodic change in th
e
displacement of elements of an
object in the direction of the long
axis of the rod
ERT 452 12

13. TRANSVERSE VIBRATIONTRANSVERSE VIBRATION
a vibration in which the element
moves to and fro in a direction
perpendicular to the direction of the
advance of the wave.
TORSIONAL VIBRATIONSTORSIONAL VIBRATIONS
Angular vibration of an object (shaft)
along its axis of rotation. Torsional
vibration is often a concern in power
transmission systems using rotating
shafts or couplings where it can
cause failures if not controlled.
13

14. CLASSIFICATION OFCLASSIFICATION OF
VIBRATIONSVIBRATIONS
ERT 452 14
• Free Vibrations
• Forced Vibrations

15. Free vibration occurs when a mechanical system is
set in motion with an initial input and allowed to
vibrate freely. Examples of this type of vibration are
pulling a child back on a swing and letting go, or
hitting a tuning fork and letting it ring. The mechanical
system vibrates at one or more of its natural
frequencies and damps down to motionlessness.
15
Free
Vibrations

16. Forced Vibration
Forced vibration is when a time-varying disturbance
(load, displacement or velocity) is applied to a
mechanical system.
The disturbance can be a periodic and steady-state
input, a transient input, or a random input. The periodic
input can be a harmonic or a non-harmonic disturbance.
Examples of these types of vibration include a washing
machine shaking due to an imbalance, transportation
vibration caused by an engine or uneven road, or the
vibration of a building during an earthquake

17. ERT 452 17
 Undamped Vibration:Undamped Vibration:
When no energy is lost or dissipated in friction or
other resistance during oscillations
 Damped Vibration:Damped Vibration:
When anyenergy is lost or dissipated in friction or
other resistance during oscillations
 LinearVibration:LinearVibration:
When all basic components of a vibratory system,
i.e. the spring, the mass and the damper behave
linearly
 NonlinearVibration:NonlinearVibration:
If anyof the components behave nonlinearly

18. • Mathematical modeling of a physical system requires
the selection of a set of variables that describes the
behavior of the system.
• The number of de g re e s o f fre e do m for a system is the
number of kinematically independent variables necessary
to completely describe the motion of every particle in the
system
DOF=1
Single degree of freedom (SDOF)
DOF=2
Multi degree of freedom (MDOF)
DEGREE OF FREEDOM(DOF)DEGREE OF FREEDOM(DOF)

19.  Examples of single degree-of-freedom systems:
19

20.  Examples of Two degree-of-freedom systems:
20

21. Examples of Three degree of freedom systems:
ERT 452 21

22. Example of Infinite number of degrees of freedom system:
Infinite number of degrees of freedom system are
termed co ntinuo us or distribute d systems.
Finite number of degrees of freedom are termed
discre te or lum pe d parameter systems.
22

23. IMPORTANT APPLICATIONSIMPORTANT APPLICATIONS
Static de fle ctio n of a BEAMat the free end is given by:
Spring Co nstant is given by:
EI
Wl
st
3
3
=δ
( )7.1
3
3
l
EIW
k
st
==
δ
23
W = mg is the weight of the mass m,
E = Young’s Modulus, and
I = moment of inertia of cross-section of beam

24. SPRING ELEMENTSSPRING ELEMENTS
Combination of Springs:
1 ) Spring s in paralle l– if we have n spring constants k1, k2, …,
kn in paralle l, then the equivalent spring constant keq is:
( )11.121 ... neq kkkk +++=
24

25. Combination of Springs:
2) Spring s in se rie s – if we have n
spring constants k1, k2, …, kn in
se rie s, then the equivalent spring
constant keq is:
( )17.1
1
...
111
21 neq
kkkk
+++=
25

26. 26
DAMPINGDAMPING
The Diminishing of vibrations with time is called
Damping.

27. • Damping is the conversion of mechanical energy
of a structure into thermal energy.
• The amount of energy dissipated is a measure of
the structure’s damping level.
• Damping is very important with earthquakes
since it dissipates the destructive energy of an
earthquake which will help reduce the damage to
the building.

28. TYPES OF DAMPINGTYPES OF DAMPING
Viscous Damping:
Damping force is proportional to the velocity of
the vibrating body in a fluid medium such as air,
water, gas, and oil.
Coulomb or Dry Friction Damping:
Damping force is constant in magnitude but
opposite in direction to that of the motion of the
vibrating body between dry surfaces.
Material or Solid or Hysteretic Damping:
Energy is absorbed or dissipated by material
during deformation due to friction between
internal planes.
28

29. Hysteresis loop for elastic materials:
29

30. The more is the hysteresis in the stress-strain
curve, the greateris the energy dissipation, and
hence the higheris the damping ability.

32. • Damping is the decrease in amplitude with time due to
the resistance of the mediumto the vibration.
• Damping occurs progressively as energy is taken out
of the systemby anotherforce such as friction.
• If the damping is enough that the systemjust fails to
oscillate, then it is said to be critically damped.
Damping more than this is referred to as overdamping
and less is similarly underdamped.
OBSERVATIONSOBSERVATIONS

33. SOURCES
• Wikipedia
• Google
• NPTEL
• Enotes
• Britannica
• Theory of machines by S S Rattan
ERT 452 33

34. 34