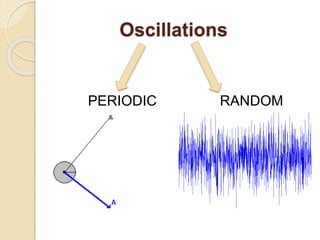
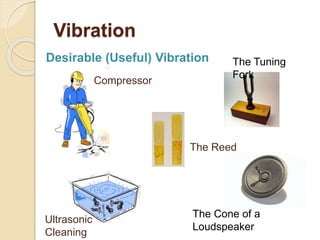
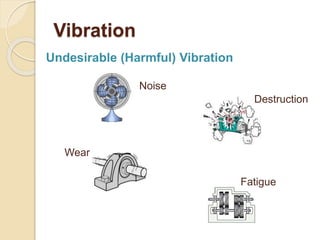
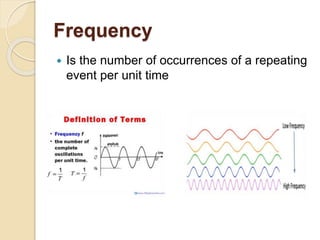
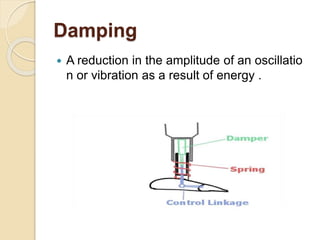
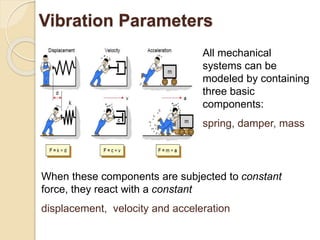
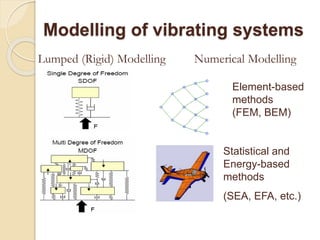
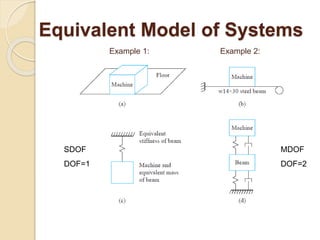
This document provides an introduction to mechanical vibration. It defines vibration as a continuous slight shaking movement and defines mechanical vibration as the measurement of periodic oscillations around an equilibrium point. It discusses different types of vibration including free undamped, free damped, forced damped, forced undamped, and vibration of multi degree of freedom systems. Key concepts discussed include periodic motion, natural frequency, damping, resonance, stiffness, and inertia. Models for analyzing vibration including lumped modeling and finite element modeling are also introduced.

1. Introduction to Mechanical Vibration
Eng.Eslam Mersal
Eng.Salma Osama
Supervised By Dr.Abdelrady Okasha

2. What is vibration?
 A continuous slight shaking movement : a series of
small, fast movements back and forth or from side
to side .

3. Definition of Mechanical
Vibration
 Mechanical vibration is defined as the
measurement of a periodic process of
oscillations with respect to an equilibrium point.

4. Oscillatory Motion
 Is the Motion Backward and Forward in a
Circular Arc .

5. Oscillations
PERIODIC RANDOM

6. Vibration
 It is also an everyday
phenomenon we meet on
everyday life.

7. Vibration
Desirable (Useful) Vibration
Compressor
Ultrasonic
Cleaning
The Tuning
Fork
The Reed
The Cone of a
Loudspeaker

8. Vibration
Undesirable (Harmful) Vibration
Noise
Destruction
Wear
Fatigue

9. Vibration
More often, vibration is undesirable,
wasting energy and creating unwanted
sound – noise!
The vibrational motions of
engines, electric motors,
other mechanical devices
which are usually the
results of imbalance in
rotating parts, uneven
friction, meshing gear, etc.
are typically unwanted!

10. Definitions
 Periodic motion: A motion which repeats itself after equal
intervals of time.
 Time period: Time taken to complete one cycle.
 Frequency: Number of cycles per unit time.
 Amplitude: The maximum displacement of a vibrating body
from its equilibrium position.
 Natural frequency: When no external force acting on the
system after giving it an initial displacement, the body
vibrates. These vibrations are called free vibrations and their
frequency as natural frequency. It is expressed in rad/sec or
Hertz.
 Fundamental Mode of Vibration: The fundamental mode of
vibration of a system is the mode having the lowest natural
frequency.
 Damping: is the resistance to the motion of vibrating body.
 Resonance: when the frequency of external excitation is

11. Periodic Motion
 When the same motion repeats itself after
equal intervals of time .

12. Frequency
 Is the number of occurrences of a repeating
event per unit time

13. Natural Frequency
 Is the frequency at which a system tends
to oscillate in the absence of any driving
or damping force

14. Damping
 A reduction in the amplitude of an oscillatio
n or vibration as a result of energy .

15. Resonance
 Is a phenomenon in which a vibrating system or
external force drives another system to oscillate
with greater amplitude at a specific preferential
frequency .

16. Stiffness
 The extent to which it resists deformation in
response to an applied force .

17. Inertia
 Is the resistance of any physical object to
any change in its state of motion; this
includes changes to its speed, direction or
state of rest .

18. Simple Harmonic Motion
 The motion of a body about a fixed
point is called simple harmonic
motion.
 The motion is periodic.
 The motion of a simple pendulum is
simple harmonic in nature.
 A body having simple harmonic motion
is represented by the equation.
X=Asin(wt)

19. Vibration Parameters
All mechanical
systems can be
modeled by containing
three basic
components:
spring, damper, mass
When these components are subjected to constant
force, they react with a constant
displacement, velocity and acceleration

20. Lumped (Rigid) Modelling Numerical Modelling
Element-based
methods
(FEM, BEM)
Statistical and
Energy-based
methods
(SEA, EFA, etc.)
Modelling of vibrating systems

21. Degree of Freedom (DOF)
• The number of degrees of freedom for a system is
the number of kinematically independent variables
necessary to completely describe the motion of
every particle in the system.
DOF=1
Single degree of freedom (SDOF)
DOF=2
Multi degree of freedom (MDOF)

22. Equivalent Model of Systems
Example 1: Example 2:
SDOF
DOF=1
MDOF
DOF=2

23. Types of Vibration
 Free undamped vibration
 Free damped vibration
 Forced damped vibration
 Forced undamped vibration
 Forced damped vibration under
harmonic motion of the base
 Vibration of multi degree of freedom
systems

24. Free Vibration
Equilibrium pos.
 When a system is initially disturbed by a displacement,
velocity or acceleration, the system begins to vibrate
with a constant amplitude and frequency depend on
its stiffness and mass.
 This frequency is called as natural frequency, and
the form of the vibration is called as mode shapes

25. Forced Vibration
If an external force applied to a
system, the system will follow the
force with the same frequency.
However, when the force
frequency is increased to the
system’s natural frequency,
amplitudes will dangerously
increase in this region. This
phenomenon called as
“Resonance”
’

26. Damped Vibration
When the energy of a vibrating system is gradually
dissipated by friction and other resistances, the
vibrations are said to be damped. The vibrations
gradually reduce or change in frequency or intensity
or cease and the system rests in its equilibrium
position

27. Thanks