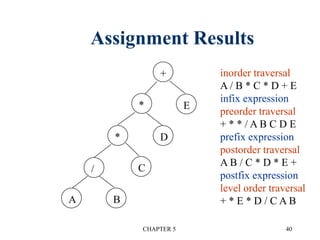
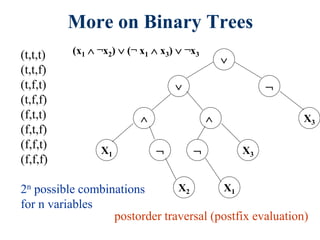
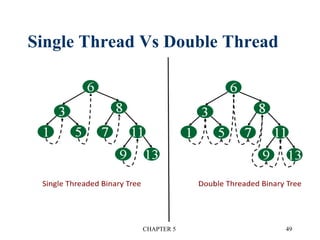
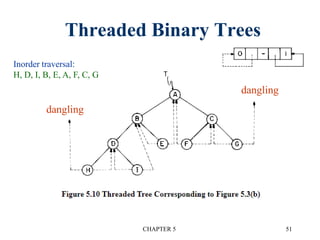
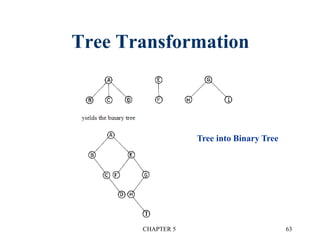
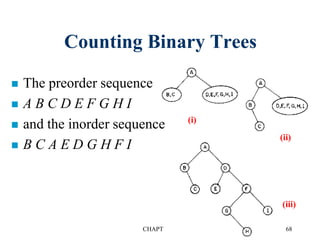
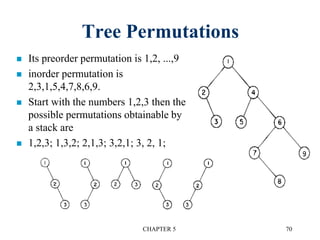
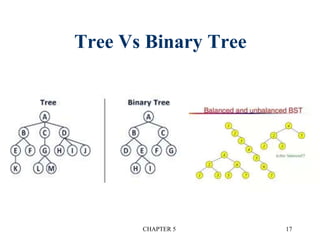
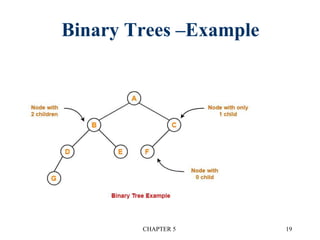
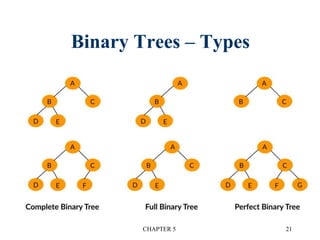
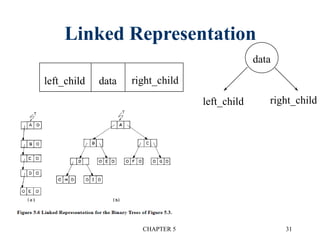
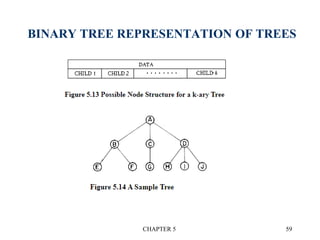
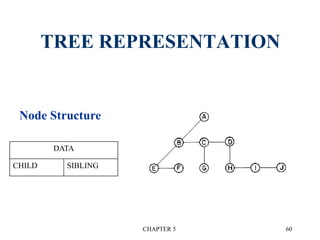
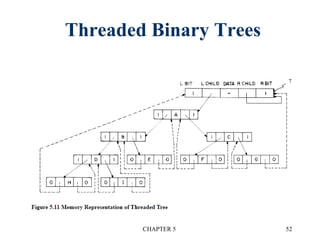
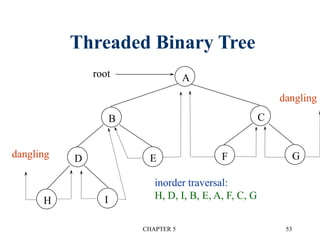
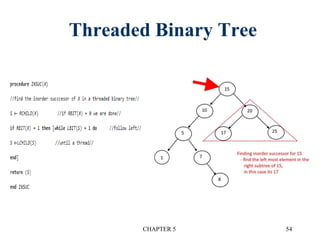
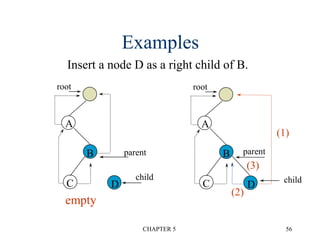
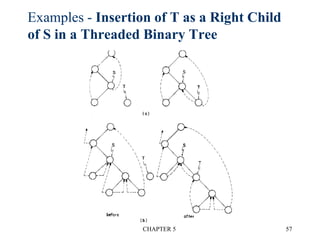
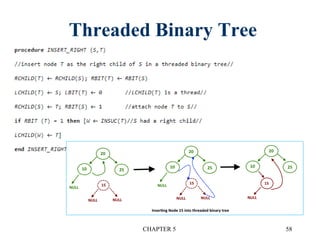
There are three main types of binary tree representations: 1. Sequential representation stores nodes in arrays sequentially. It wastes space and has problems with insertion/deletion. 2. Linked representation stores a data field and left/right child pointer fields in each node. 3. Threaded binary trees reduce wasted space by replacing null pointers with "threads" to other nodes. This allows traversal without recursion.

1. CHAPTER 5
Trees
Dr. R. Khanchana
Assistant Professor
Department of Computer Science
Sri Ramakrishna College of Arts and Science for Women
http://icodeguru.com/vc/10book/books/book1/chap05.htm

2. Tree
 A Tree Structure means that the data is
organized so that items of information are
related by branches.
CHAPTER 5 2

3. Genealogical Chart Types
CHAPTER 5 3
Pedigree Chart
Two way Branching

4. Genealogical Chart Types
CHAPTER 5 4
Lineal Chart

5. CHAPTER 5 5
Definition of Tree
 A tree is a finite set of one or more nodes
such that:
 There is a specially designated node called
the root.
 The remaining nodes are partitioned into n>=0
disjoint sets T1, ..., Tn, where each of these sets
is a tree.
 We call T1, ..., Tn the subtrees of the root.

6. CHAPTER 5 6
Terminology
 Node stands for the item of information plus the branches
to other items.
 The degree of a node is the number of subtrees of the
node.
– The degree of A is 3; the degree of C is 1.
 The node with degree 0 is a leaf or terminal node. Other
nodes are nonterminal nodes.
 A node that has subtrees is the parent of the roots of the
subtrees.
 The roots of these subtrees are the children of the node.
 Children of the same parent are siblings.

7. Terminology
 The ancestors of a node are all the nodes along the
path from the root to the node.
 The degree of a tree is the maximum degree of the
nodes in the tree.
 The height or depth of a tree is defined to be the
maximum level of any node in the tree.
 The level of a node is defined by initially letting the
root be at level one.
 If a node is at level l then its children are at level l + 1
 A forest is a set of n>=0 disjoint trees. If we remove
the root of a tree we get a forest.
CHAPTER 5 7

8. CHAPTER 5 8
Forest
 A forest is a set of n >= 0 disjoint trees
A E G
B C D F H I G
H
I
A
B
C
D
F
E
Forest

9. CHAPTER 5 9
Trees

10. Level
CHAPTER 5 10

11. Depth
CHAPTER 5 11

12. Representation of Trees
CHAPTER 5 12

13. CHAPTER 5 13
Representation of Trees
 List Representation
– ( A ( B ( E ( K, L ), F ), C ( G ), D ( H ( M ), I, J ) ) )
– The root comes first, followed by a list of sub-trees
data link 1 link 2 ... link n
How many link fields are
needed in such a representation?

14. CHAPTER 5 14
Left Child - Right Sibling
A
B C D
E F G H I J
K L M
data
left child right sibling

15. Representation of Trees
CHAPTER 5 15

16. Quiz
CHAPTER 5 16
https://quizizz.com/admin/quiz/5f4390b3d43729001baf44e1

17. Tree Vs Binary Tree
CHAPTER 5 17

18. CHAPTER 5 18
Binary Trees
 Definition: A binary tree is a finite set
of nodes that is either empty or consists
of a root and two disjoint binary trees
called the left subtree and the right
subtree.
 Any tree can be transformed into binary
tree.
– by left child-right sibling representation
 The left subtree and the right subtree are
distinguished.

19. Binary Trees –Example
CHAPTER 5 19

20. Binary Trees – Types
CHAPTER 5 20

21. Binary Trees – Types
CHAPTER 5 21

22. CHAPTER 5 22
Samples of Trees
A
B
A
B
A
B C
GE
I
D
H
F
Complete Binary Tree
Skewed Binary Tree
E
C
D
1
2
3
4
5

23. Binary Trees
CHAPTER 5 23

24. CHAPTER 5 24
Maximum Number of Nodes in BT
 Lemma –5.1
 The maximum number of nodes on level i of a
binary tree is 2i-1, i>=1.
 The maximum nubmer of nodes in a binary tree
of depth k is 2k-1, k>=1.
Prove by induction.
2 2 11
1
i
i
k
k

  

25. CHAPTER 5 25
Relations between Number of
Leaf Nodes and Nodes of Degree 2
Lemma –5.2
For any nonempty binary tree, T, if n0 is the
number of leaf nodes and n2 the number of nodes
of degree 2, then n0=n2+1
proof: Let n and B denote the total number of nodes &
branches in T.
Let n0, n1, n2 represent the nodes with no children,
single child, and two children respectively.
n= n0+n1+n2, B+1=n, B=n1+2n2 ==> n1+2n2+1= n,
n1+2n2+1= n0+n1+n2 ==> n0=n2+1

26. CHAPTER 5 26
Full BT VS Complete BT
 A full binary tree of depth k is a binary tree of
depth k having 2 -1 nodes, k>=0.
 A binary tree with n nodes and depth k is
complete iff its nodes correspond to the nodes
numbered from 1 to n in the full binary tree of
depth k.
k
A
B C
GE
I
D
H
F
A
B C
GE
K
D
J
F
IH ONML
Full binary tree of depth 4
Complete binary tree

27. Quiz
 https://quizizz.com/admin/quiz/5f449b8b68
3fb6001b5efd76
CHAPTER 5 27

28.  A full binary tree of depth k is a binary tree
of depth k having 2k - 1 nodes.
 A binary tree with n nodes and of
depth k is complete iff its nodes correspond
to the nodes which are numbered one to n in
the full binary tree of depth k
CHAPTER 5 28
Binary Tree Representations

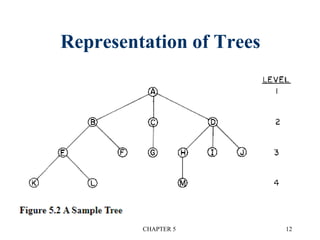
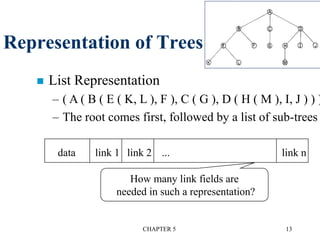
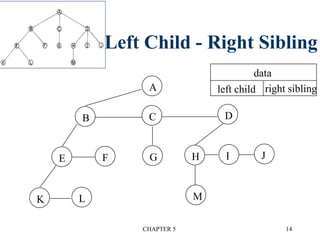
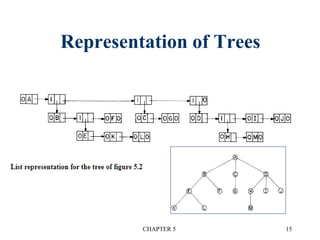
29. CHAPTER 5 29
Binary Tree Representations
Lemma 5.3: If a complete binary tree with n nodes (i.e.,
depth= [log2n] + 1) is represented sequentially as above
then for any node with index i, 1 i n we have:
(i) PARENT(i) is at [i/2] if i 1. When i = 1, i is the root
and has no parent.
(ii) LCHILD(i) is at 2i if 2i n. If 2i > n, then i has no
left child.
(iii) RCHILD(i) is at 2i + 1 if 2i + 1 n. If 2i + 1 > n,
then i has no right child.

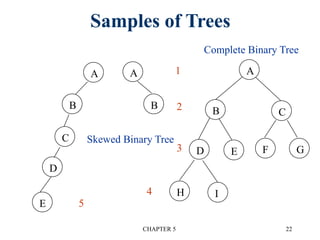
30. CHAPTER 5 30
Sequential Representation
A
B
--
C
--
--
--
D
--
.
E
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
.
[16]
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
A
B
C
D
E
F
G
H
I
A
B
E
C
D
A
B C
GE
I
D
H
F
(1) waste space
(2) insertion/deletion
problem

31. CHAPTER 5 31
Linked Representation
dataleft_child right_child
data
left_child right_child

32. CHAPTER 5 32
Binary Tree Traversals
 Let L, D, and R stand for moving left, Printing
the data, and moving right.
 There are six possible combinations of traversal
– LDR, LRD, DLR, DRL, RDL, RLD
 Adopt convention that we traverse left before
right, only 3 traversals remain
– LDR, LRD, DLR
– inorder, postorder, preorder

33. Binary Tree Traversals
CHAPTER 5 33

34. Binary Tree Traversals
CHAPTER 5 34

35. InOrder Tree Traversals
CHAPTER 5 35
Output
A/B ** C * D + E

36. PreOrder Tree Traversals
CHAPTER 5 36
Output
+* / A ** B C D E

37. PostOrder Tree Traversals
CHAPTER 5 37
Output
A B C ** / D * E +

38. CHAPTER 5 38
Assignment
+
*
A
*
/
E
D
C
B
Inorder traversal ?
Preorder traversal ?
Postorder traversal ?

39. Quiz
CHAPTER 5 39
https://quizizz.com/admin/quiz/5f53582fac018d001b325a30

40. CHAPTER 5 40
Assignment Results
+
*
A
*
/
E
D
C
B
inorder traversal
A / B * C * D + E
infix expression
preorder traversal
+ * * / A B C D E
prefix expression
postorder traversal
A B / C * D * E +
postfix expression
level order traversal
+ * E * D / C A B

41. More on Binary Trees
CHAPTER 5 41

42. More on Binary Trees
CHAPTER 5 42

43. More on Binary Trees- X1, I, J, Z, FST, X2, K
CHAPTER 5 43

44. More on Binary Trees
CHAPTER 5 44

45. 


X3X1
X2 X1
 X3
(x1  ¬x2)  (¬ x1  x3)  ¬x3(t,t,t)
(t,t,f)
(t,f,t)
(t,f,f)
(f,t,t)
(f,t,f)
(f,f,t)
(f,f,f)
2n possible combinations
for n variables
postorder traversal (postfix evaluation)
More on Binary Trees

46. LCHILD DATA VALUE RCHILD
More on Binary Trees - Node structure

47. More on Binary Trees
CHAPTER 5 47

48. CHAPTER 5 48
Threaded Binary Trees
 Two many null pointers in current representation
of binary trees
n: number of nodes
number of non-null links: n-1
total links: 2n
null links: 2n-(n-1)=n+1
 Replace these null pointers with some useful “threads”.

49. Single Thread Vs Double Thread
CHAPTER 5 49

50. Advantages of Threaded BST
 Thread is pointer to other nodes in the tree to
replace null links.
CHAPTER 5 50

51. Threaded Binary Trees
CHAPTER 5 51
Inorder traversal:
H, D, I, B, E, A, F, C, G
dangling
dangling

52. Threaded Binary Trees
CHAPTER 5 52

53. CHAPTER 5 53
Threaded Binary Tree
A
B C
GE
I
D
H
F
root
dangling
dangling
inorder traversal:
H, D, I, B, E, A, F, C, G

54. Threaded Binary Tree
CHAPTER 5 54

55. Threaded Binary Tree
CHAPTER 5 55

56. CHAPTER 5 56
Examples
root
parent
A
B
C D
child
root
parent
A
B
C D child
empty
Insert a node D as a right child of B.
(1)
(2)
(3)

57. Examples - Insertion of T as a Right Child
of S in a Threaded Binary Tree
CHAPTER 5 57

58. Threaded Binary Tree
CHAPTER 5 58

59. BINARY TREE REPRESENTATION OF TREES
CHAPTER 5 59

60. TREE REPRESENTATION
CHAPTER 5 60
DATA
CHILD SIBLING
Node Structure

61. Associated Binary Tree
CHAPTER 5 61

62. Tree Vs Binary Tree
CHAPTER 5 62

63. Tree Transformation
CHAPTER 5 63
Tree into Binary Tree

64. Tree Transformation
CHAPTER 5 64
Define this transformation in a formal way as follows:
If T1, ...,Tn is a forest of trees, then the binary tree
corresponding to this forest, denoted by B(T1, ..., Tn):
(i) is empty if n = 0;
(ii) has root equal to root (T1); has left subtree equal
to B(T11,T12, ...,T1m) where T11, ..., T1m are the subtrees
of root(T1); and has right subtree B(T2, ..., Tn).

65. Tree Transformation
CHAPTER 5 65
Preorder traversal of T is equivalent to visiting the nodes of F in tree
preorder which is defined by:
(i) if F is empty then return;
(ii) visit the root of the first tree of F;
(iii) traverse the subtrees of the first tree in tree preorder;
(iv) traverse the remaining trees of F in tree preorder.
Inorder which is defined by:
(i) if F is empty then return;
(ii) traverse the subtrees of the first tree in tree inorder;
(iii) visit the root of the first tree;
(iv) traverse the remaining trees in tree inorder.
postorder which is defined by:
(i) if F is empty then return;
(ii) traverse the subtrees of the first tree of F in tree postorder;
(iii) traverse the remaining trees of F in tree postorder;
(iv) visit the root of the first tree of F.

66. Quiz
CHAPTER 5 66
https://quizizz.com/admin/quiz/5f53574a41c5a0001b1467dd

67. Counting Binary Trees
 The number of distinct binary trees having n nodes.
 If n = 0 or n = 1 there is one such tree.
 If n = 2, then there are two distinct binary trees
 and if n = 3, there are five
CHAPTER 5 67

68. Counting Binary Trees
 The preorder sequence
 A B C D E F G H I
 and the inorder sequence
 B C A E D G H F I
CHAPTER 5 68
(i)
(ii)
(iii)

69. Tree Permutations
 A permutation is an arrangement in a particular
order of a group of items.
 Let the nodes of an n node binary tree be
numbered 1 to n.
 The inorder permutation defined by such a
binary tree is the order in which its nodes are
visited during an inorder traversal of the tree.
 A preorder permutation is similarly defined.
CHAPTER 5 69

70. Tree Permutations
 Its preorder permutation is 1,2, ...,9
 inorder permutation is
2,3,1,5,4,7,8,6,9.
 Start with the numbers 1,2,3 then the
possible permutations obtainable by
a stack are
 1,2,3; 1,3,2; 2,1,3; 3,2,1; 3, 2, 1;
CHAPTER 5 70

71. Matrix Multiplication
 A product of n matrices
M1 * M2 * M3 * ... * Mn
 For example, if n = 3, there are two possibilities
(M1 * M2) * M3 and M1 * (M2 * M3)
 and if n = 4, there are five ways
((M1 * M2) * M3) * M4, (M1 * (M2 * M3)) * M4,
M1 * ((M2 * M3) * M4)
(M1 * (M2 * (M3 * M4))), ((M1 * M2) * (M3 * M4))
CHAPTER 5 71

72. Matrix Multiplication
 Let bn be the number of different ways to
compute the product of n matrices.
Then b2 = 1, b3 = 2, b4 = 5. Let Mij, i j, be
the product Mi * Mi+1 * ... * Mj.
CHAPTER 5 72

73. CHAPTER 5 73