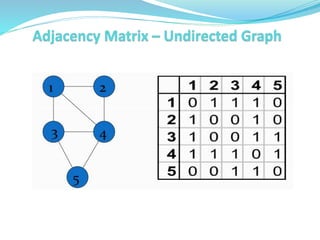
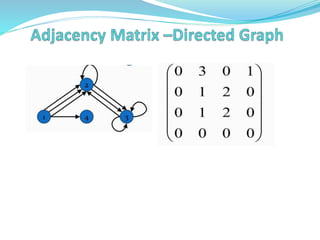
The document defines graphs and discusses their properties and applications. It covers topics like directed vs undirected graphs, representations using adjacency matrices and lists, graph traversals using depth-first and breadth-first search, minimum spanning trees, and applications of graphs in areas like social networks and the world wide web.

1.  Graphs are collections of nodes connected by edges
G = (V,E) where V is a set of nodes and E a set of
edges.
 Graphs are useful in a number of applications
– Shortest path problems
– Maximum flow problem
 Graphs unlike trees are more general for they can
have connected components.

2.  Directed Graphs: A directed graph edges allow
travel in one direction. graph
 Undirected Graphs: An undirected edges allow
travel in either direction

3. A graph is an ordered pair G=(V,E) with a set of
vertices or nodes and the edges that connect them.
 A subgraph of a graph has a subset of the vertices
and edges.
 The edges indicate how we can move through the
graph.
 A path is a subset of E that is a series of edges
between two nodes.
 A graph is connected if there is at least one path
between every pair of nodes.

4. The length of a path in a graph is the number of edges in
the path.
 A complete graph is one that has an edge between
every pair of nodes.
 A weighted graph is one where each edge has a cost for
traveling between the nodes.
 A cycle is a path that begins and ends at the same node.
 An acyclic graph is one that has no cycles.
An acyclic, connected graph is also called an unrooted
tree

5. Number of Edges – Undirected Graph
 The no. of possible pairs in an n vertex graph is n*(n-1)
 Since edge (u,v) is the same as edge (v,u), the number of
edges in an undirected graph is n*(n- 1)/2.
Number of Edges - Directed Graph
 The no. of possible pairs in an n vertex graph is n*(n-1)
 Since edge (u,v) is not the same as edge (v,u), the number
of edges in a directed graph is n*(n-1)
 Thus, the number of edges in a directed graph is ≤ n*(n-1)

6. For graphs to be computationally useful, they
have to be conveniently represented in programs
 There are two computer representations of
graphs:
 Adjacency matrix (Sequential representation)
 Adjacency lists ( Linked representation)

7. A square grid of boolean values
If the graph contains N vertices, then the grid
contains N rows and N columns.
 For two vertices numbered I and J, the element at
row I and column J is true(0) if there is an edge from I
to J, otherwise false(1).

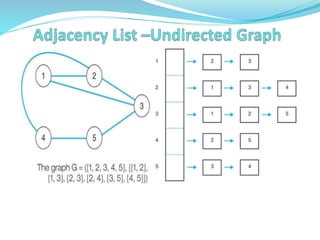
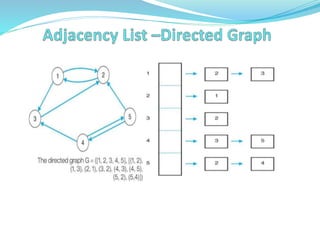
10. In an adjacency list, the n rows of the adjacency list are
represented as n-linked lists, one list per vertex of the graph
 A graph of n nodes is represented by a one dimensional array L
of linked lists, where
● L[i] is the linked list containing all the nodes adjacent from
node i.
● The nodes in the list L[i] are in no particular order.
For a weighted graph, this list would also include the weight for
each edge.

13.  Some algorithms require that every vertex of a graph
be visited exactly once.
 The order in which the vertices are visited may be
important, and may depend upon the particular
algorithm.
 The two common traversals:
- depth-first
- breadth-first

14. DFS starts at the vertex v of G as a start vertex and v is
marked as visited .
 Then, each unvisited vertex adjacent to v is searched
using the DFS recursively Once all the vertices that
can be reached from v have been visited, the search of
v is complete.
 If some vertices remain unvisited, we select an
unvisited vertex as a new start vertex and then repeat
the process until all the vertices of G are marked
visited

15. The order of the
depth-first traversal
of this graph starting
at node 1 would be:
1, 2, 3, 4, 7, 5, 6, 8, 9

16. In BFS, all the unvisited vertices adjacent to i are visited
after visiting the start vertex i and marking it visited.
Next, the unvisited vertices adjacent to these vertices are
visited and so on until the entire graph has been traversed.
 From the starting node, we follow all paths of length
one.
 Then we follow paths of length two that go to unvisited
nodes.
 We continue increasing the length of the paths until
there are no unvisited nodes along any of the paths.

17. The order of the
breadth-first traversal
of this graph starting
at node 1 would be:
1, 2, 8, 3, 7, 4, 5, 9, 6

18.  A tree is a connected graph with no cycles
 A spanning tree is a sub-graph of G that has all
vertices of G and is a tree
 A minimum spanning tree of a weighted graph G is
the spanning tree of G whose edges sum to
minimum weight

19. Spanning trees (a) Graph (b) Spanning tree
(c) Minimum spanning tree

20. An undirected graph is connected if there is at least
one path between every pair of vertices in the graph
 A connected component of a graph is a maximal
connected subgraph, that is, every vertex in a
connected component is reachable from the vertices in
the component

21. This figure shows
the Sample graph with
one connected component
 This figure shows the Graph
with two connected components

22.  Prim’s algorithm starts from one vertex and grows
the rest of the tree by adding one vertex at a time, by
adding the associated edges
This algorithm builds a tree by iteratively adding
edges until a minimal spanning tree is obtained, that
is, when all nodes are added
 At each iteration, it adds to the current tree a vertex
though minimum weighted edge that does not
complete a cycle.

23.  Minimum Spanning tree using Prim’s algorithm.

24.  Another way to construct a minimum spanning tree
for a graph G is to start with a graph T = (V′, E′ = ø)
consisting of the n vertices of G and having no edges.
 In Prim’s algorithm, we start with one connected
component, add a vertex to have one connected
component and no cycles, and end up with one
connected component
 Here, we start with n connected components; at each
step, the number of connected components would
reduce by one and end up with one connected
component

25. The shortest path between
two given vertices is the path
having minimum length.

26. In Computer science graphs are used to represent the
flow of computation.
Google maps uses graphs for building transportation
systems.
In Facebook, users are considered to be the vertices and if
they are friends then there is an edge running between them.
This is an undirected graph

27. In World Wide Web, web pages are considered to be the
vertices. There is an edge from a page u to other page v if there is
a link of page v on page u. This is an example of Directed graph.
In Operating System, we come across the Resource Allocation
Graph where each process and resources are considered to be
vertices. Edges are drawn from resources to the allocated process,
or from requesting process to the requested resource. If this
leads to any formation of a cycle then a deadlock will occur.

28. The number of elements in the adjacency matrix of a graph
having 7 vertices is __________
a) 7 b) 14 c) 36 d) 49
What would be the number of zeros in the adjacency matrix of
the given graph?
a) 10 b) 6 c) 16 d) 0
 A graph with all vertices having equal degree is known as a __
a) Multi Graph b) Regular Graph
c) Simple Graph d) Complete Graph