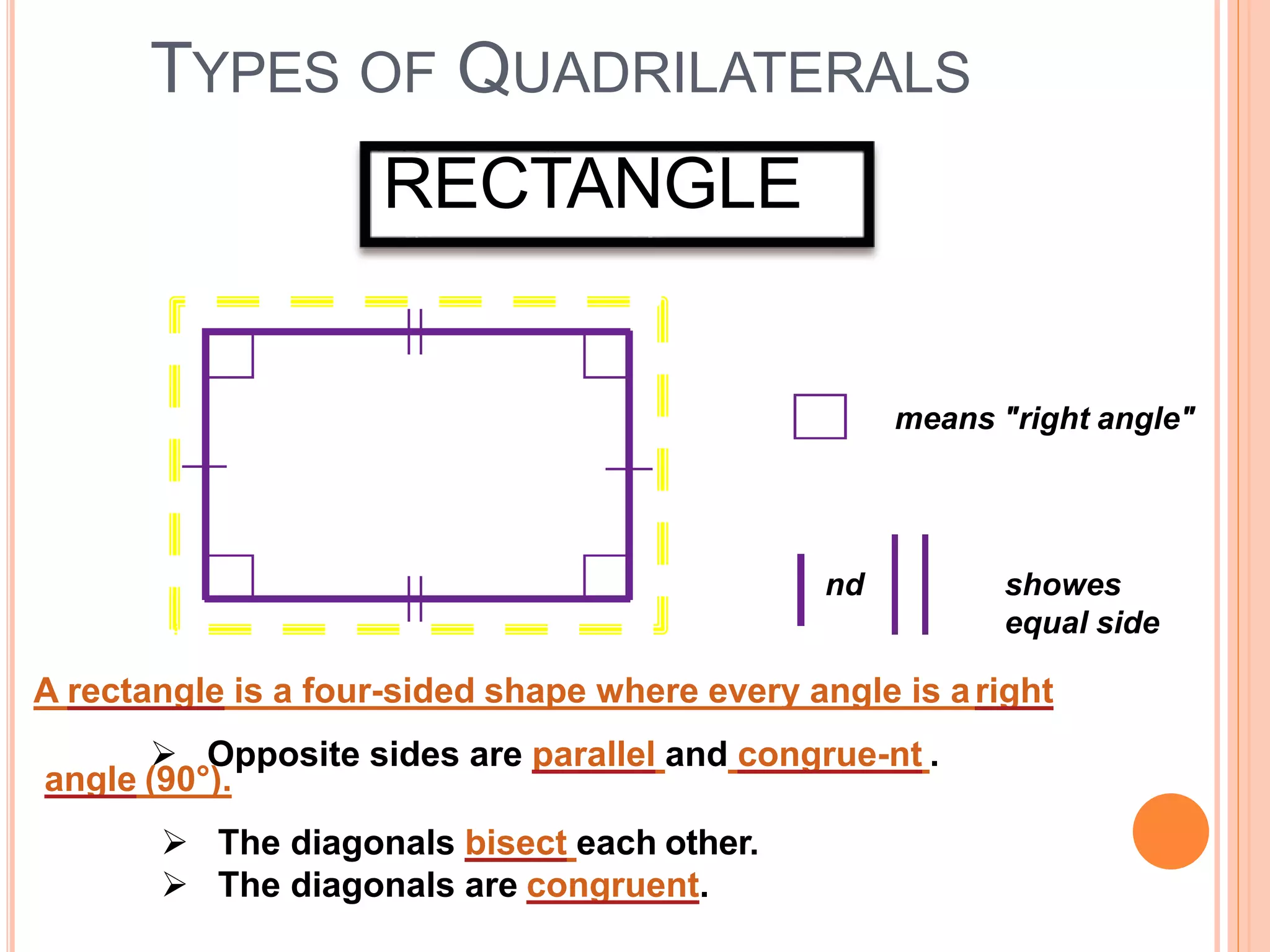
The document discusses different types of polygons and quadrilaterals. It defines a polygon as a closed plane figure bounded by three or more straight sides that meet at vertices. Quadrilaterals are polygons with four sides. There are several types of quadrilaterals including rectangles, squares, rhombi, parallelograms, trapezoids, and kites. The document provides properties and definitions for each type of quadrilateral.

2. CURVES
 Aplanecurveis acurve that lies in asingle plane or aplane
surfacelike paper.Aplane curve may beclosed or open.

3. POLYGONS
Polygon is a closed
plane figure bounded by
three or more straight sides
that meet in pairs in the same
number of vertices, and do
not intersect other than at
these vertices.

4. PARTS OF APOLYGON
- The endpoints of the sidesof polygons are called vertices.
When naming a polygon, its vertices are named in
consecutive order either clockwise or counterclockwise.
- Consecutivesides are two sidesthat have an endpoint in common.
The four-sided polygon in Figure below could have beennamed
ABCD,BCDA,or ADCB,for example. It doesnot matter with which
letter you begin aslong asthe vertices are named consecutively.
SidesABand BCare examples of consecutive sides.
There are four pairs of consecutive sidesin this polygon.

5. PARTS OF APOLYGON
ADIAGONAL OF APOLYGON IS ANY SEGMENT THAT JOINS TWO
NONCONSECUTIVE VERTICES. FIGURE SHOWS FIVE-SIDED POLYGON
QRSTU.SEGMENTS QS,SU,UR,RTAND QTARE THE DIAGONALS IN
THIS POLYGON.
Diagonalsof a polygon can be found with the formula given below :

7. CLASSIFICATION OFPOLYGONS
Polygons first fit into twogeneral
categories—convexand notconvex
(sometimes called concave).
Apolygon is concave if there are two
points somewhere inside it for whicha
segmentwith theseasits endpoints
cuts at least 2 of the sidesof the
polygon.
Apolygon that is not concave is called
convex

8. CLASSIFICATION OFPOLYGONS

9. CLASSIFICATION OFPOLYGONS
Polygons are also classified by how many sides (or angles or
vertices) they have. The following lists the different types of
polygons and the number of sidesthat they have:
Atriangle is athree-sided polygon
Aquadrilateral is afour-sided polygon.
Apentagonis afive-sided polygon.
Ahexagonis asix-sided polygon.
Aseptagonor heptagon is aseven-sided polygon.
An octagonis an eight-sided polygon.
Anonagonis anine-sided polygon.
Adecagonis aten-sided polygon

10. REGULAR POLYGONS
When apolygon is both equilateral and equiangular, it is referred
to asaregular
polygon.For apolygon to beregular, it must also be convex.
.

11. SUMOF INTERIOR ANGLES OF POLYGON
Sumof the interior anglesof apolygon =(N - 2) x180°
Note: Sumofexterioranglesofanypolygonisalways360 degrees &the
sumofinterior anglesofapolygoncanbemoreorlessthan 360 degrees
whichcanbecalculatedbytheformulagiven above.

15. AQuadrilateral is any shapewith 4 sides.Theword
“quadrilateral” comes from two Latin words “quadri” which
means ‘a variant of four’ and “lateral” which means side.
PROPERTIES:
 with four sides
 with four angles
 with four vertices
 With one pair of diagonals
QUADRILATERALS

16.  Interior AngleSumProperty: According to this property, the
sum of the interior angles of the quadrilateral is 360°
 ExteriorAngle SumProperty: According to this property, the
sum of the exterior angles of the quadrilateral is 360°
QUADRILATERALS

17. QUADRILATER
ALS
Rectangle
Parallelogram
Rhombus
Square
Isosceles
Trapezoid
Kite
Quadrilateral
(Trapezium)
Trapezoid

18. TYPES OF QUADRILATERALS
RECTANGLE
means "right angle"
and showes
equal sidesid
 The diagonals bisect each other.
 The diagonals are congruent.
A rectangle is a four-sided shape where every angle is aright
 Opposite sides are parallel and congrue-nt .
angle (90°).

20. RHOMBUS
A rhombus is a four-sided shape where all sides haveequal
length.
 Also opposite sides are parallel and opposite angles are equal.
Another interesting thing is that the diagonals (dashed lines in
second figure) of a rhombus bisect each other at right angles.

21. SQUARE
means "right angle"
show equal sides
A square has equal sides and every angle is a rightangle (90°)

23. PARALLELOGRAM
A parallelogram is a quadrilateral with
opposite sides parallel. Also opposite
angles are equal (angles "a“ is same as
angles "b“ ). The opposite sides are
equal .The adjacent angles are
supplementary and the diagonals
bisects each other ; but they are not
equal.

25. TRAPEZIUM
Trapezium Isosceles Trapezium
A trapezium is quadrilateral which has at least one pair ofparallel
sides
It is called an Isosceles trapezium if the sides that aren'tparallel
are equal in length and both angles coming from a parallel side are
equal
Note : Trapezium is UK terminology & in US terminology it is called as
Trapezoid

27. KITE
 A kite is a quadrilateral
whose four sides can be
grouped into two pairs of
equal-length sides that are
adjacent to each other.
 Kite quadrilaterals are
named for the wind-
blown, flying kites, which
often have this shape

28.  Two pairs of adjacent sides of a kite are equal
in length
One pair of opposite angles (the ones that
are between the sides of unequal length)
are equal in size.
 One diagonal bisects the other.
 Diagonals intersect at right angles.

29. QUADRILATERALS