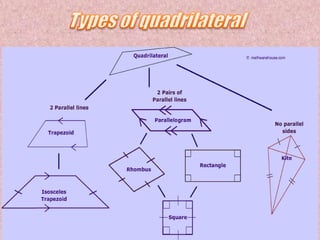
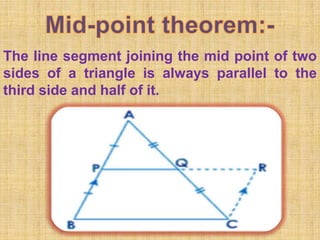
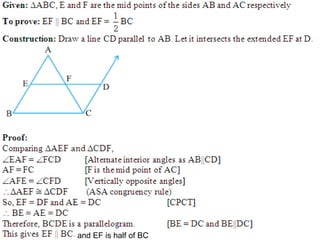
We gratefully acknowledge our maths teacher for helping us prepare this PowerPoint presentation on types of quadrilaterals. The document then defines and describes the key properties of various quadrilaterals including parallelograms, rectangles, squares, rhombi, trapezoids, kites, and the use of midpoints and diagonals to prove geometric theorems.

2. We all gratefully acknowledge the valuable
contributions of our respected MATHS TEACHER as
without her we won`t be able to prepare this
PowerPoint presentation of Maths.
Our special thanks for her support
and her precious knowledge that made us able to
accomplish this task.

3. A Quadrilateral is an enclosed 4 sided figure which has 4
vertices and 4 angles.
There are two types of quadrilaterals and they are:-
 Convex quadrilateral:-
A quadrilateral whose all four angles sum upto 360 degree
and diagonals intersect interior to it
 Concave quadrilateral:-
A quadrilateral whose sum of four angles is more than 360
degrees and diagonals intersect interior to it.
 There are many types of quadrilaterals which have
many different properties.

5. A quadrilateral with opposite sides parallel and
equal is a parallelogram .
Properties:-
• A diagonal of a parallelogram divides it into
two congruent triangles.
•In a parallelogram, opposite sides are equal.
•In a parallelogram opposite angles are equal.
•The diagonals of a parallelogram bisect each
other.
These properties have their converse also.

6. A rectangle is a parallelogram with one angle 90 degree
The properties of rectangle are:-
The diagonals of rectangle are of equal length.
It has including properties of parallelogram.
It has two pairs of opposite sides equal.
The opposite sides of rectangle are parallel to each other.

7. A square is a rectangle with adjacent sides
equal. The properties of a square are:-
Square has including properties of
Rectangle
Diagonals of a
square bisect each other at 90
Degrees and are equal.
The all four interior angles of square are
right angles.

8. A Rhombus is a parallelogram with adjacent
sides equal. The properties of rhombus are:-
A rhombus has the including properties of
A parallelogram.
The diagonals of rhombus bisect each other at 90 degree
The diagonals of rhombus bisect opposite angles

9. A trapezium is quadrilateral with one pair of opposite sides parallel and
other sides are non parallel
PROPERTIES OF TRAPEZIUM ARE:-
Co-interior angles of parallel sides of trapezium are supplementary
Sum of the angles of trapezium are 360 degree.

10. A quadrilateral with two pairs of adjacent sides
equal is known as a kite. Properties of kite are:-
The diagonals of a kite bisect each other 90
degree.
Adjacent sides of a kite are equal.
The smaller diagonal bisect the angles of kite.
Sum of angles of kite is 360 degree.

11. The line segment joining the mid point of two
sides of a triangle is always parallel to the
third side and half of it.

12. Given:-D and E are the mid points of the sides AB
and AC .
To prove:-DE is parallel to BC and DE is half of
BC.
construction:- Construct a line parallel to AB
through C.
proof:-in triangle ADE and triangle CFE
AE=CE
angle DAE= angle FCE (alternate angles )
angle AED= angle FEC (vertically opposite

13. Hence by CPCT AD= CF- - - - - - - - -1
But
AD = BD(GIVEN)
so from (1), we get,
BD = CF
BD is parallel to CF
Therefore BDFC is a parallelogram
That is:- DF is parallel to BC and DF= BC
Since E is the mid point of DF
DE= half of BC, and , DE is parallel to BC
Hence proved .

14. According to the converse of mid point theorem
the line drawn through the mid point of one side
of a triangle, is parallel to another side bisects the
third side.
WE CAN PROVE THE CONVERSE OF
THE MID POINT THEOROM THROUGH
THE EXPLANATION IN THE NEXT SLIDE .

15. and EF is half of BC