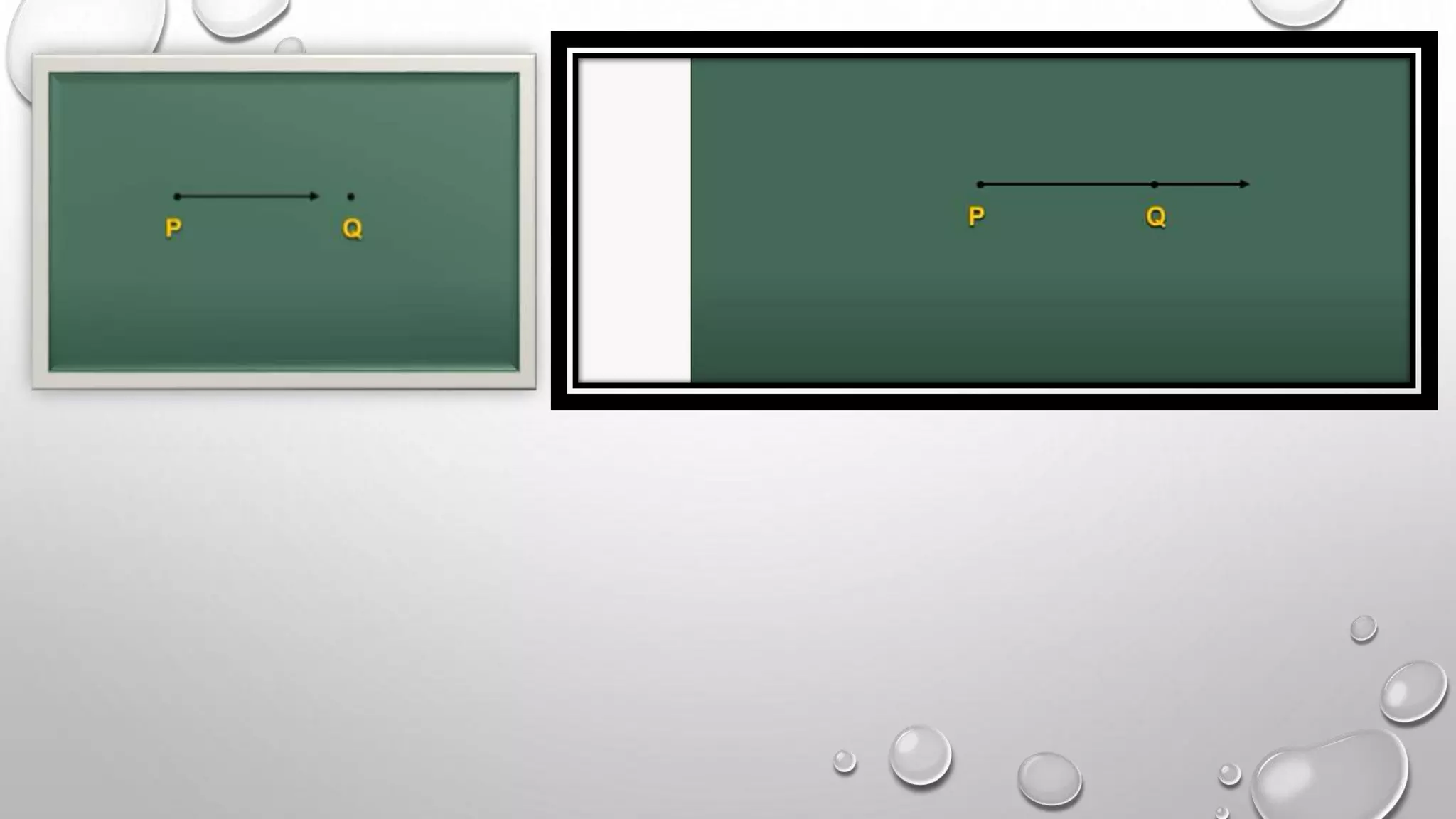
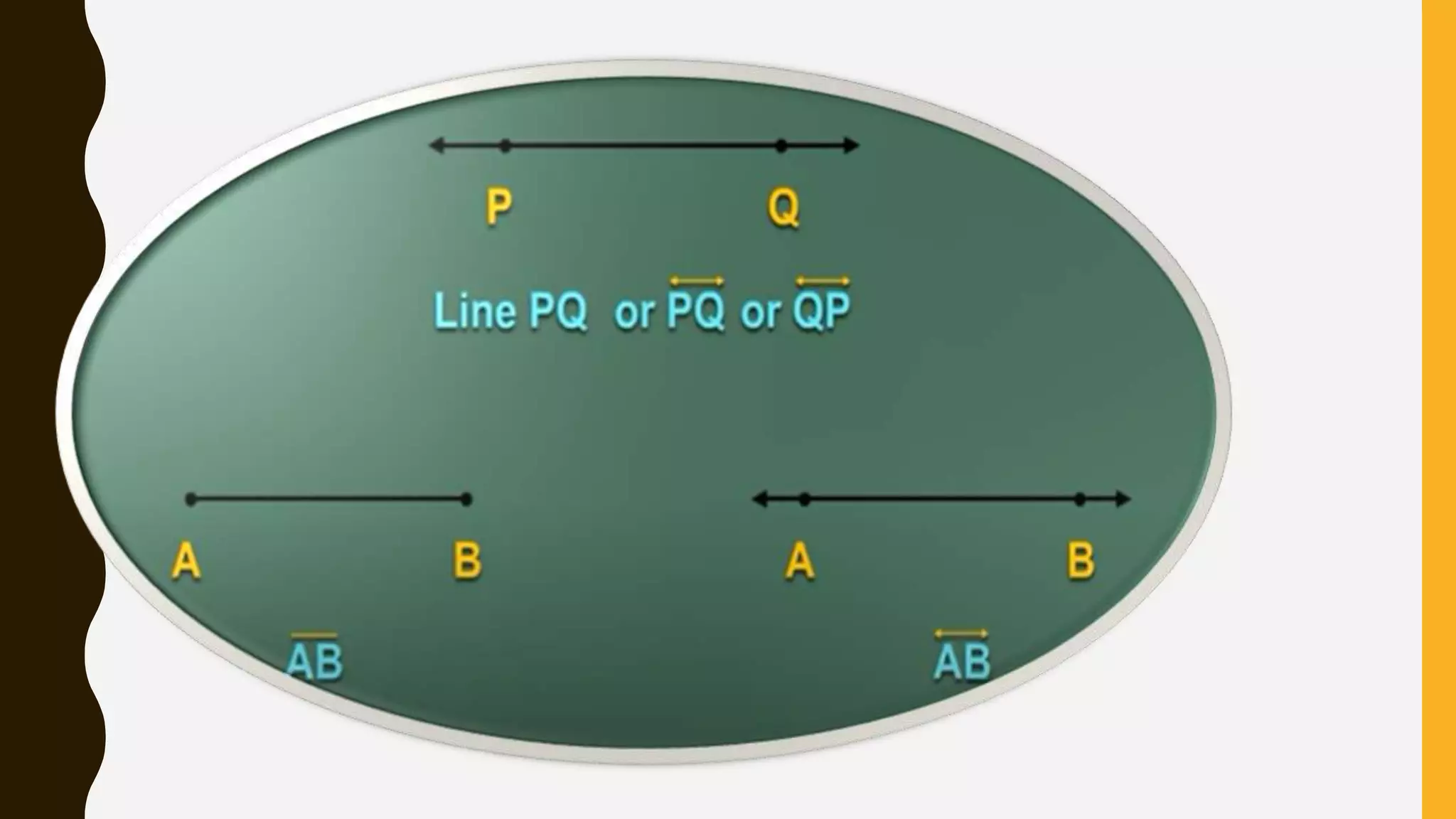
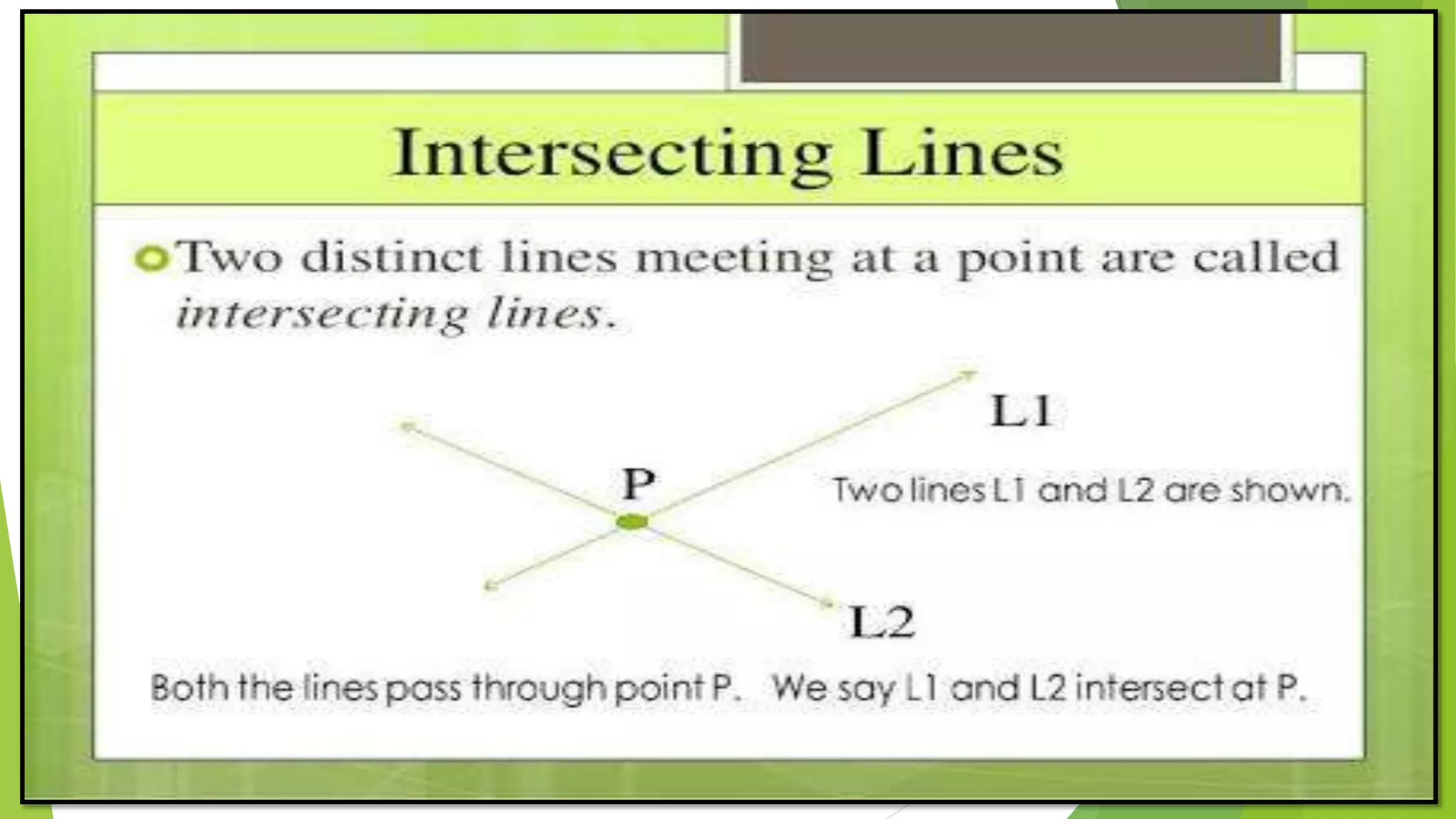
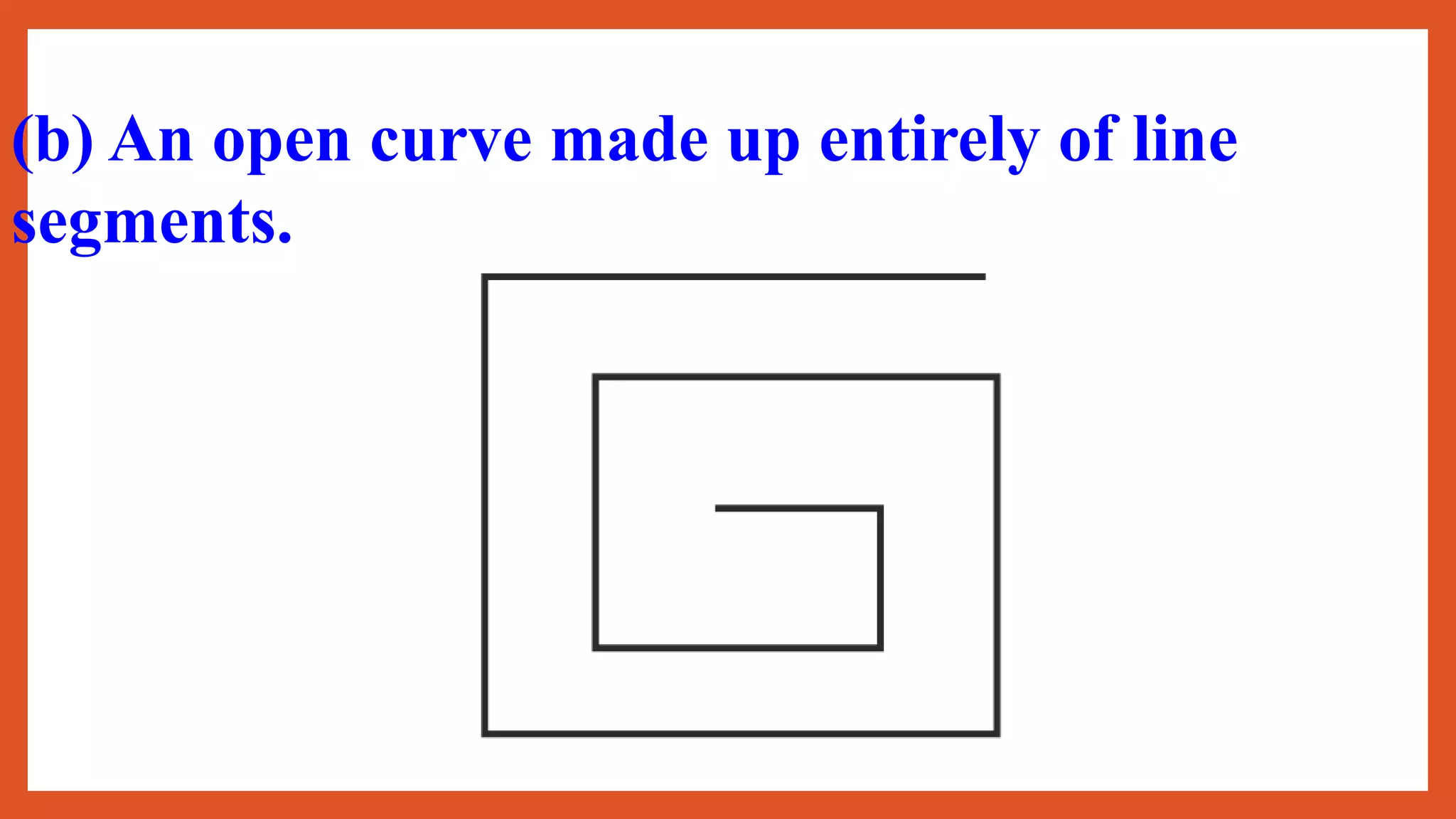
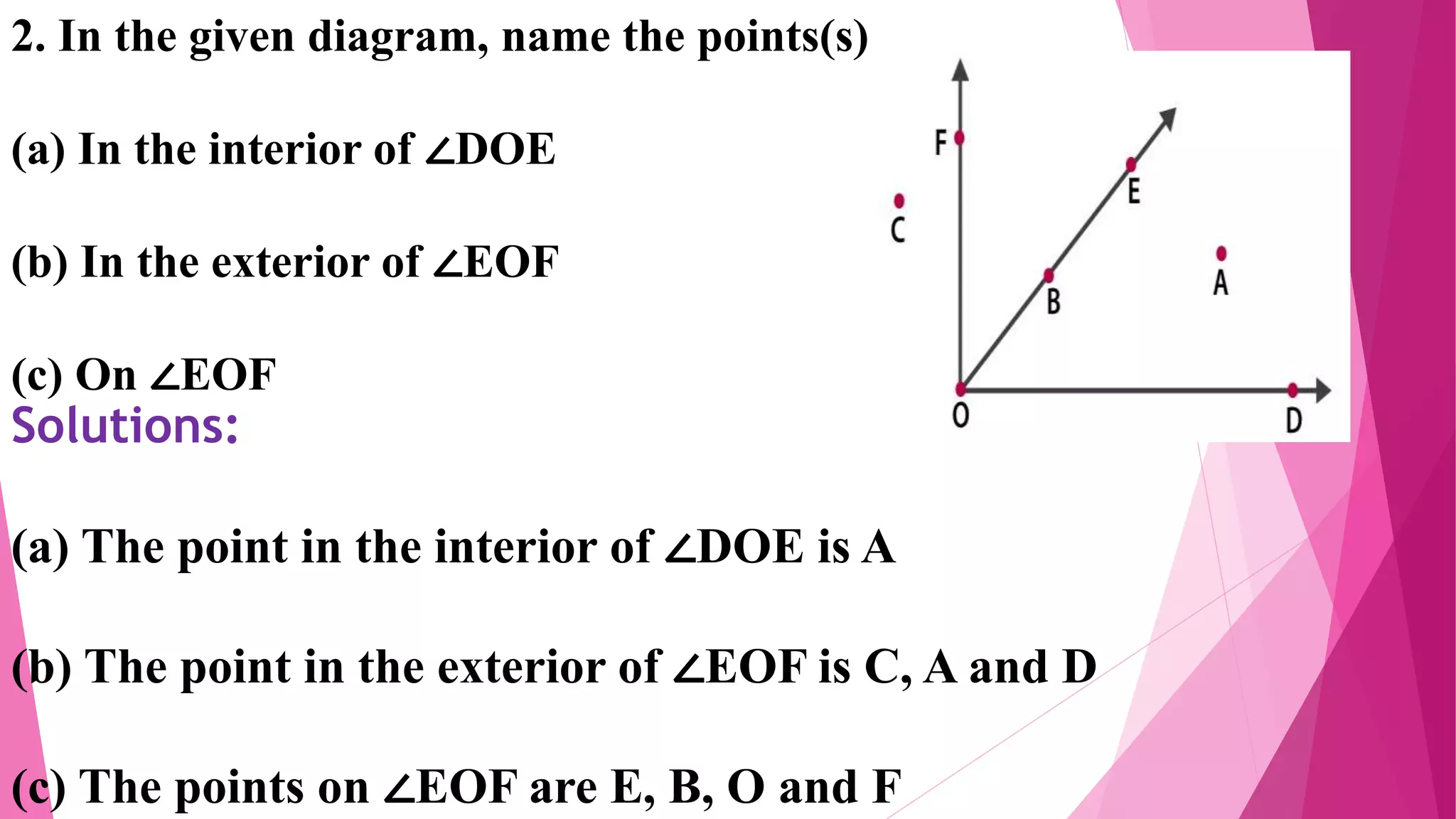
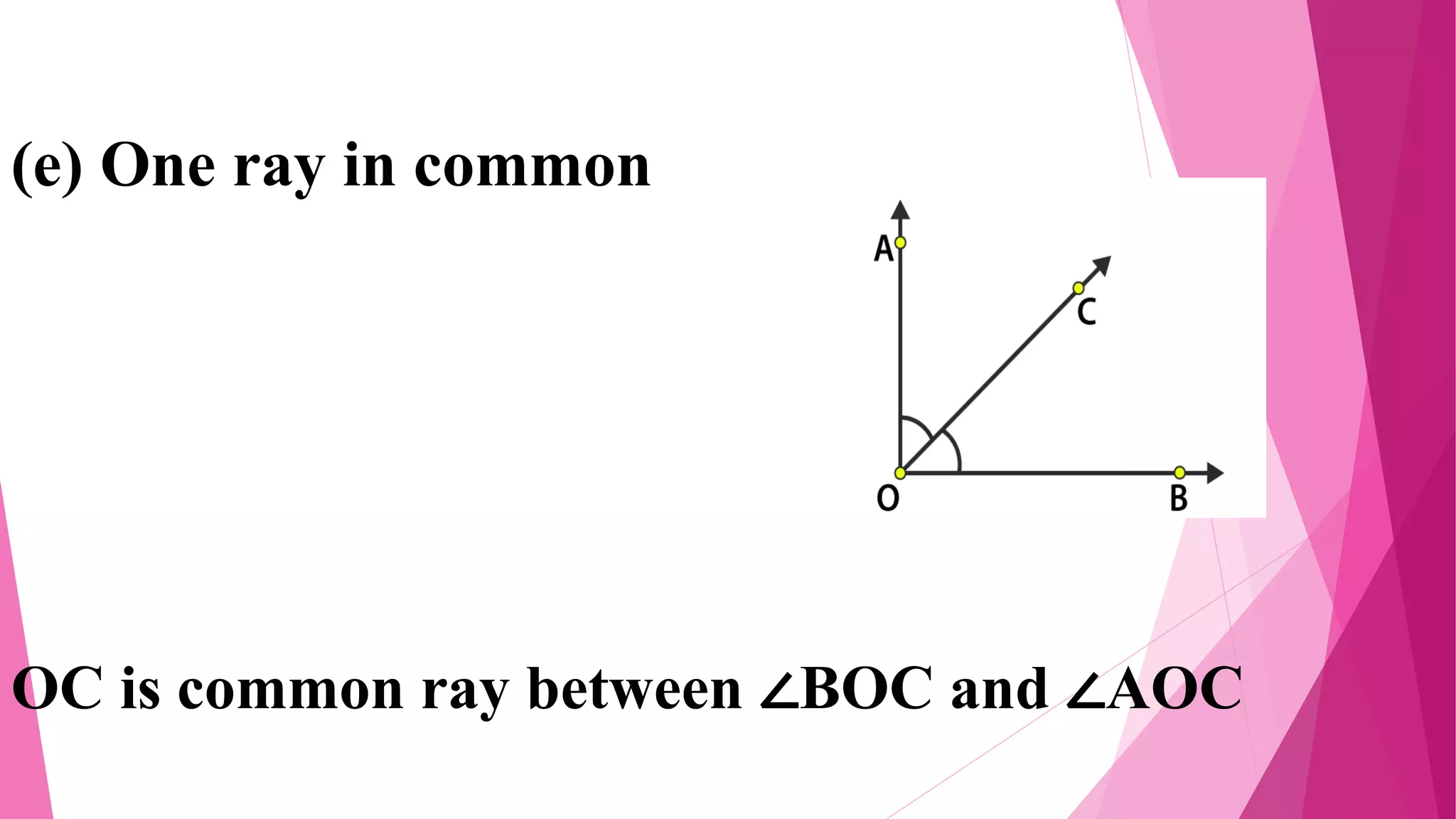
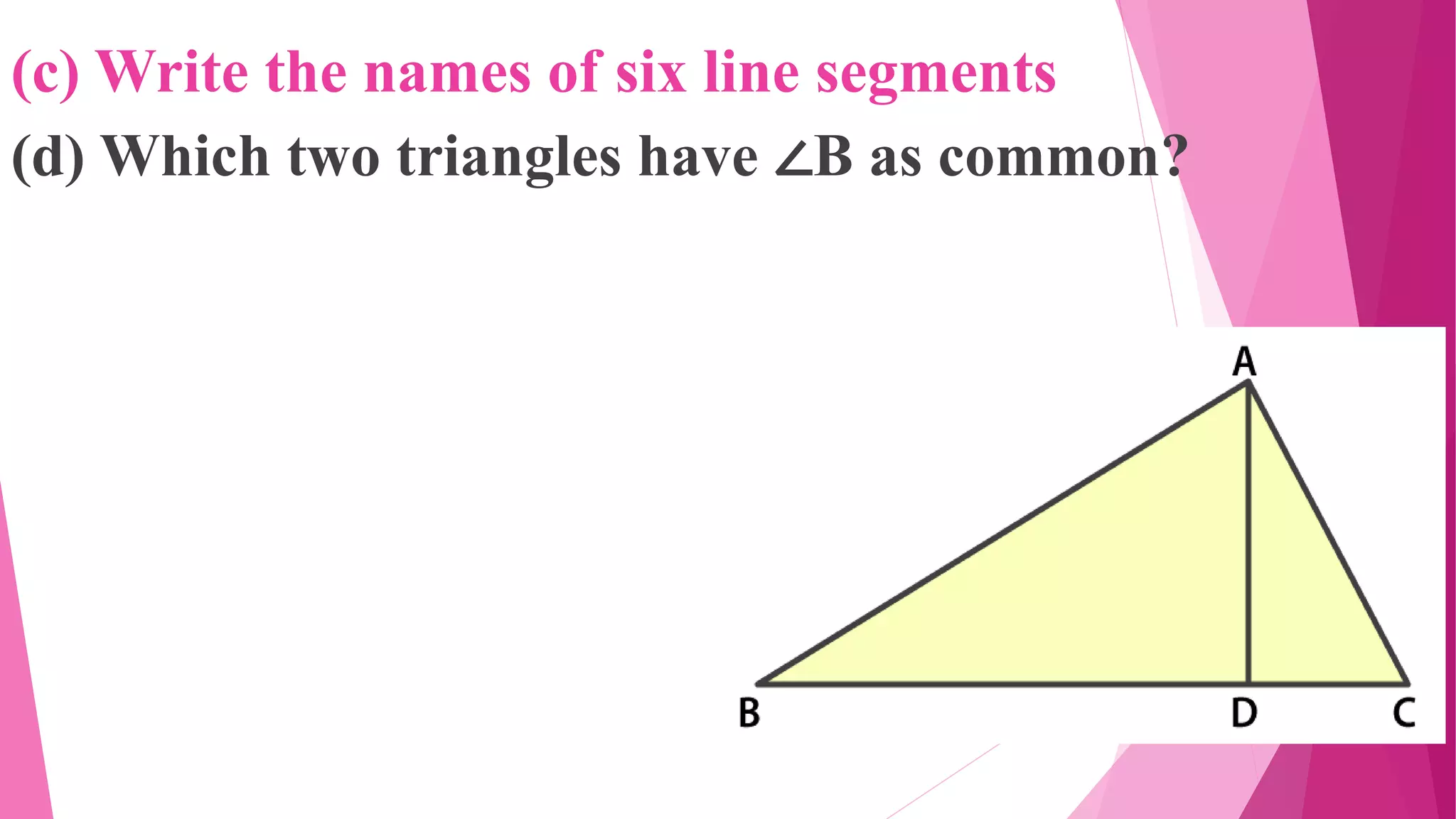
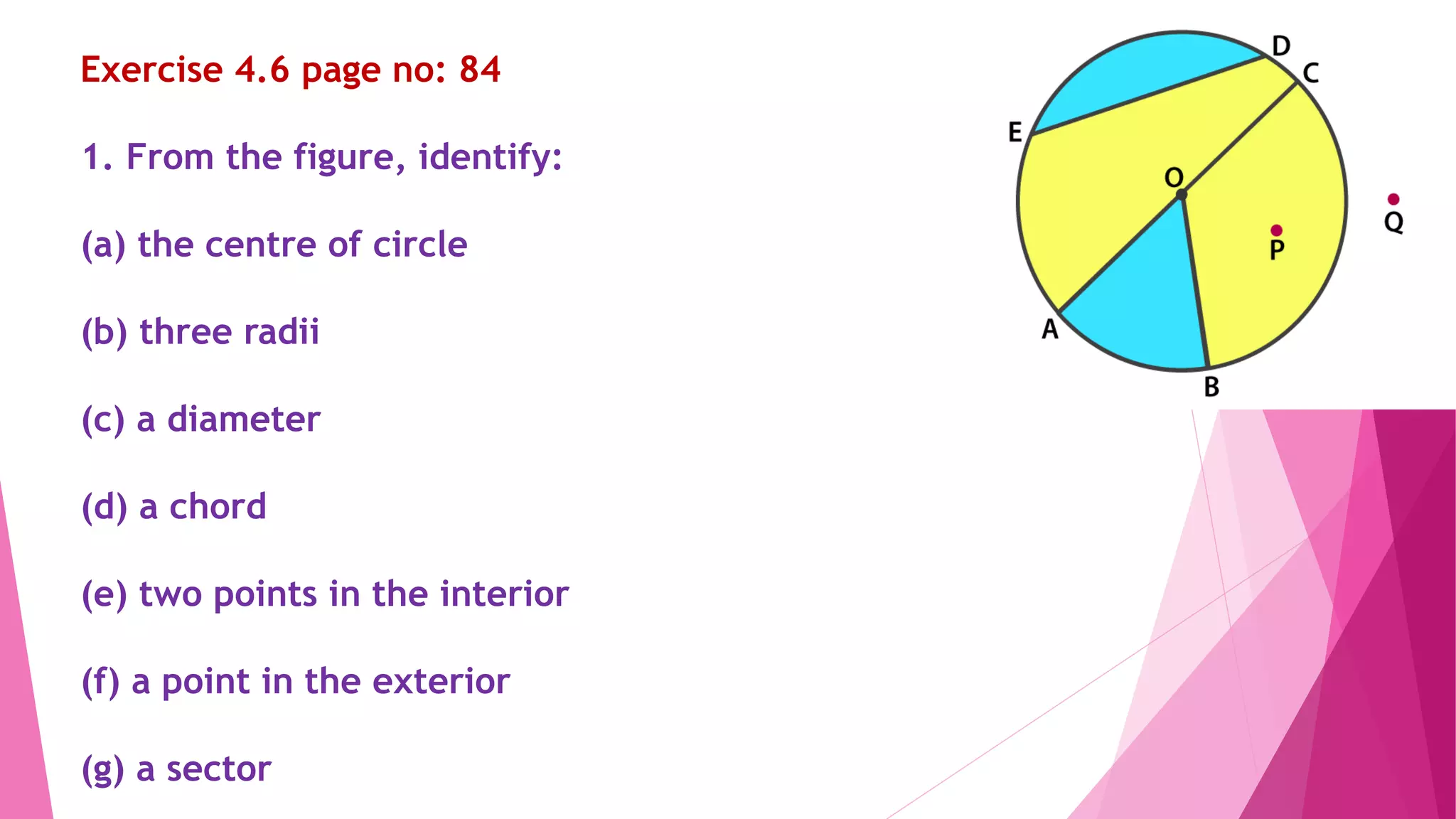
This document provides an overview of basic geometrical concepts including points, lines, curves, polygons, angles, triangles, quadrilaterals, and circles. It begins with definitions of points, lines, and line segments. It then covers intersecting and parallel lines, rays, curves (simple, closed, and open), and polygons. Key details about angles, triangles, quadrilaterals, and circles are also summarized, along with examples and exercises related to each topic.

1. CHAPTER-4
BASIC
GEOMETRICAL
IDEAS

3. POINTS TO BE COVERED:
• Points
• Line Segment
• Line
• Intersecting lines
• Parallel lines
• Ray
• Curves
• Polygons

4. INTRODUCTION:
The term ‘Geometry’ is the Greek word ‘Geometron’.
Geo’ means Earth and ‘metron’ means Measurement.
According to historians, the geometrical ideas shaped up the
ancient times.
• The boundaries of cultivated lands had to be marked
without giving room for complaints.
• Construction of magnificent palaces, temples, lakes,dams
and cities, art and architecture propped up thee ideas.

8. A point determines a location.
It is denoted by a single capital
letter A,B,C etc.

25. EXERCISE: 4.1:
1.

26. Solution:
(a) O, E, D, B, C
(b) DB
© Four rays:
OC , OB, OE, OD
(d) Five line segments:
OE, ED, OC, OB, OD

27. 2. Name the line given in all possible (twelve) ways,
choosing only two letters at a time from the four given:

30. 3. Use the figure to name:
a)Line containing point E.
AE
b) Line passing through A
AE
c) Line on which O lies:
CO
d) Two pairs of intersecting lines:
AE and CO, AE and FE

31. 4. How many lines can pass through
(a)one given point?
Countless lines can pass through one given point.
(b) Two given points?
Only one line can pass through two given points.

32. 5. Draw a rough figure and label suitably in each of the
following cases:
a) Point p Lies on AB
b) XY and PQ intersect at M.
c) Line l contains E and F but not D
d) OP and OQ meet at O.

34. Curves
• Any drawing (straight or non-straight ) done without
lifting the pencil may be called as curve

35. Types
•Simple curves : A
simple curve is one
that does not cross
itself
•Closed curve: A curve
is said to be closed if
its ends are joined ;
otherwise it is said to
be open

36. In closed curve there are 3 parts
I) interior of the curve
Ii) boundary of the curve
Iii) exterior of the curve

37. POLYGONS
• The line segments are the sides
of the polygon
• Any two side with a common
end point are adjacent sides
• The meeting point of a pair of
sides is called a vertex
• The join of any two non -
adjacent vertices is a diagonal

38. Exercise 4.2 (PAGE : 78)
1. Classify the following curves as (i) Open or
(ii) Closed

39. Solutions:
(a) The given curve is an open curve
(b) The given curve is closed curve
(c) The given curve is open curve
(d) The given curve is closed curve
(e) The given curve is closed curve

40. 2. Draw any polygon and shade its interior.

41. 3. Illustrate, if possible, each one of the following
with a rough diagram:
(a) A closed curve that is not a polygon.

42. (b) An open curve made up entirely of line
segments.

43. (c) A polygon with two sides.
No its not possible, as the polygon having least
number of sides is a triangle which has three
sides.

44. Angle:
An angle is made up of two rays starting
from a common starting/initial points.
• An angle leads to three divisions of a
region.
• On the angle
• Interior of the angle
• Exterior of the angle

45. Exercise 4.3 (page : 80)
1. Name the angles in the given figure.
Solutions:
The angles are ∠DAB, ∠ABC, ∠BCD and
∠CDA

46. 2. In the given diagram, name the points(s)
(a) In the interior of ∠DOE
(b) In the exterior of ∠EOF
(c) On ∠EOF
Solutions:
(a) The point in the interior of ∠DOE is A
(b) The point in the exterior of ∠EOF is C, A and D
(c) The points on ∠EOF are E, B, O and F

47. 3. Draw rough diagrams of two angles such that they
have
(a) One point in common
O is common point between ∠COD and ∠AOB

48. (b) Two points in common
(b) O and B are common points between ∠AOB and
∠BOC

49. (c) Three points in common
(c) O, E and B are common points between
∠AOB and ∠BOC

50. (d) Four points in common
O, E, D and A are common points between
∠BOA and ∠COA

51. (e) One ray in common
OC is common ray between ∠BOC and ∠AOC

52. TRIANGLE :
A triangle is a three sided polygon. It is a
polygon with least number of sides.
A triangle has 3 sides, 3 angles and 3 vertices
A triangle has 3 regions associated with it ,
a)On the triangle
b)The interior of the triangle
c)The exterior of the triangle

53. Exercise: 4.4page 81)
1. Draw a rough sketch of a triangle ABC. Mark a
point P in its interior and a point Q in its exterior. Is
the point A in its exterior or in its interior?
Point A lies on the
given triangle ABC.
It lies neither in
interior nor
exterior.

54. 2. (a) Identify three triangles in the figure.

55. (b) Write the names of seven angles.

56. (c) Write the names of six line segments
(d) Which two triangles have ∠B as common?

57. QUADRILATERALS:
A four sided polygon is a quadrilateral. It has 4 sides
and 4 angles and 4 vertices

58. Exercise 4.5
1. Draw a rough sketch of a quadrilateral PQRS. Draw its
diagonals. Name them. Is the meeting point of the
diagonals in the interior or exterior of the quadrilateral?
Solutions:
 PR and QS are the diagonals. They meet at point O which is
in the interior of the quadrilateral.

59. 2. Draw a rough sketch of a quadrilateral
KLMN. State,
a) two pairs of opposite sides
b) two pairs of opposite angles
c) two pairs of adjacent sides
d) two pairs of adjacent angles

61. CIRCLES
A circle is the path of a point moving at
the same distance from a fixed point
Parts of a circle
• Centre : The fixed point is called as the centre
• Radius : The line segment that connects the centre to any point on
the circle is called the radius
• Chord : A line segment joining any two points on the circle
• Diameter : A chord passing through the centre of the circle.
Diameter is twice the radius

62. • Arc : The point of a circle is called arc
• Sector : A sector is a region in the interior
of the circle enclosed by an arc on one
side and a pair of radius on the other two
sides
• Segment : It is the region in the interior
of the circle enclosed by an arc and a chord
• Circumference : The distance around the
circle is called circumference
• Diameter : It is the longest chord of the circle
and it divides the circle into two semi - circles

63. Exercise 4.6 page no: 84
1. From the figure, identify:
(a) the centre of circle
(b) three radii
(c) a diameter
(d) a chord
(e) two points in the interior
(f) a point in the exterior
(g) a sector

64. 2. a) Is every diameter of a circle also a chord ?
Yes every diameter of a circle is also a chord.
Diameter is also called as longest chord.
b) Is every chord of a circle also a diameter ?
No, every chord is not a diameter.

65. 3. Say true or false :
a) Two diameters of a circle will
necessarily intersect
 True
b) The centre of a circle is always in its
interior
 True