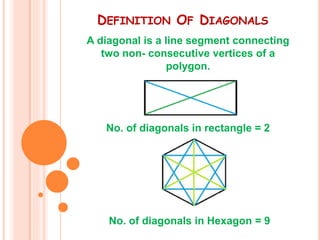
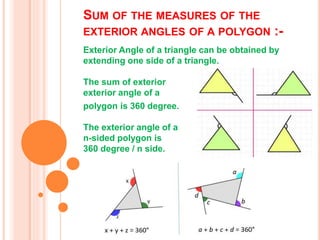
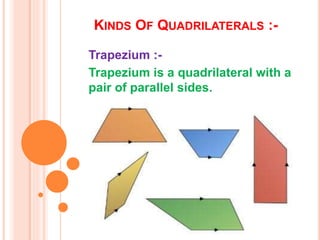
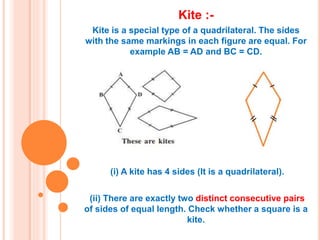
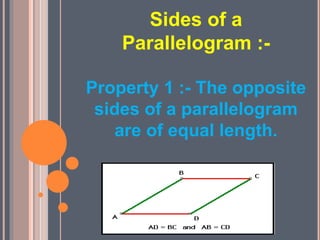
This document discusses different types of quadrilaterals. It defines polygons and quadrilaterals, and explains their properties. Some key quadrilaterals discussed include parallelograms, rectangles, squares, rhombi, and trapezoids. The document explains that parallelograms have opposite sides of equal length and opposite angles of equal measure. It further notes that rectangles are parallelograms with four right angles, while squares are rectangles with all four equal sides. The properties of diagonals and angles are also summarized for various quadrilaterals.

1. MATHS
CHAPTER – 3
CLASS – VIII
UNDERSTANDING
QUADRILATERALS
PRESENT BY –
ISHANT KUMAR

2. HERE ARE SOME PICTURES
OF QUADRILATERALS :-

3. DEFINITION OF POLYGON:-
A simple closed curve made up of only
line segments is called a polygon.
Curves that are polygons :-
Curves that are not polygons :-
Note:- The word ‘polygon’ is a Greek
word. Poly means many and gon means
angles.

4. CLASSIFICATION OF POLYGONS:-

5. DEFINITION OF DIAGONALS
A diagonal is a line segment connecting
two non- consecutive vertices of a
polygon.
No. of diagonals in rectangle = 2
No. of diagonals in Hexagon = 9

6. INTERIOR AND EXTERIOR :-
INTERIOR – THE INSIDE PART OF THE POLYGON.
EXTERIOR – THE OUTSIDE PART OF THE POLYGON.

7. CONVEX AND CONCAVE POLYGON:-
Convex Polygons :- Polygons that are
convex have no portions of their diagonals
in the exterior.
Concave Polygon :- Polygons that are
concave have portions of their diagonals in
the exterior.

8. REGULAR AND IRREGULAR POLYGON :-
Regular Polygon :- A regular polygon is
both ‘ equiangular ’ and ‘ equilateral ’. For
example, a square has sides of equal length
and equal angles of equal measure.

9. Irregular Polygon :- A irregular
polygon is not ‘ equiangular ’ and ‘
equilateral ’. For example – a
rectangle is an ‘ equiangular ’ but not
‘ equilateral ’ so it will called irregular
polygon.

10. ANGLE SUM PROPERTY
INTRODUCTION :-
We have studied the Angle Sum
Property of Triangle in previous classes..

11. PROPERTY OF INTERIOR ANGLE :-
Consider a quadrilateral ABCD.
Divide it by two triangles by diagonal AC.
We have seen in the pervious slide that sum of all
angles in a triangle measure 180 degree by the
Angle Sum Property of it.

12. There were two triangles that we have seen
in the ABCD quadrilateral.
One triangle was ADC and other was ABC.
So, we know that All Angle Sum Measures of
one triangle is 180 degree.
Then two All Angle Sum Measures will be 360
degree.
WE OBSEREVE THAT :-

14. Polygons with ‘n’
sides :-
For a polygon having n
sides, (n-2) triangles
can be formed.
The sum of interior
angles of a polygon
having n sides =
(n-2)×180 degree

15. SUM OF THE MEASURES OF THE
EXTERIOR ANGLES OF A POLYGON :-
Exterior Angle of a triangle can be obtained by
extending one side of a triangle.
The sum of exterior
exterior angle of a
polygon is 360 degree.
The exterior angle of a
n-sided polygon is
360 degree / n side.

16. KINDS OF QUADRILATERALS :-
Trapezium :-
Trapezium is a quadrilateral with a
pair of parallel sides.

17. Kite :-
Kite is a special type of a quadrilateral. The sides
with the same markings in each figure are equal. For
example AB = AD and BC = CD.
(i) A kite has 4 sides (It is a quadrilateral).
(ii) There are exactly two distinct consecutive pairs
of sides of equal length. Check whether a square is a
kite.

18. PARALLELOGRAM :-
A parallelogram is a
quadrilateral whose opposite
sides are parallel.

19. ELEMENTS OF A PARALLELOGRAM :-
AB and DC, are opposite sides. AD and BC form
another pair of opposite sides. ∠A and ∠C are a pair
of opposite angles; another pair of opposite angles
would be ∠B and ∠D. AB and BC are adjacent sides.
This means, one of the sides starts where the other
ends. AB and BC are adjacent sides. This means, one
of the sides starts where the other ends. ∠A and ∠B
are adjacent angles. They are at the ends of the same
side. ∠B and ∠C are also adjacent.

20. Sides of a
Parallelogram :-
Property 1 :- The opposite
sides of a parallelogram
are of equal length.

21. ANGLES OF A
PARALLELOGRAM :-
Property 2 :- The opposite
angles of a parallelogram
are of equal measure.

22. Property 3 :- The
adjacent angles in a
parallelogram are
supplementary.

23. DIAGONALS OF A
PARALLELOGRAM :-
Property 4 :- The
diagonals of a
parallelogram bisect
each other.

24. DIFFERENCE BETWEEN
INTERSECTION AND BISECTION :-
Intersection :- Intersect means crossing or touching a
line in any ratio.
Bisection :- Bisect means cutting or touching lines in
equal ratio.

25. SOME SPECIAL PARALLELOGRAMS :-
Rhombus :-
A rhombus is a quadrilateral with sides of
equal length. So, a rhombus has all the
properties of a parallelogram and also that
of a kite.
Property : The diagonals of a rhombus are
perpendicular bisectors of one another.

26. RECTANGLE
A rectangle is a parallelogram with equal angles.
Each angle of a rectangle is a right angle. So, a
rectangle is a parallelogram in which every angle is
a right angle. Being a parallelogram, the rectangle
has opposite sides of equal length and its diagonals
bisect each other.
Property: The diagonals of a rectangle are of equal
length.

27. This is easy to justify. If ABCD is a rectangle, then
looking at triangles ABC and ABD separately, we
have –
∆ ABC ≅ ∆ ABD
This is because AB = AB (Common)
BC = AD ( Opposite Sides )
m ∠A = m ∠B = 90° ( Opposite Angles )
The congruency follows by SAS criterion.
Thus AC = BD
and in a rectangle the diagonals, besides being equal
in length bisect each other.

28. SQUARE :-
A square is a rectangle with equal sides.
A square has all the properties of a rectangle
with an additional requirement that all the sides
have equal length.
The square, like the rectangle, has diagonals of
equal length.
BELT is a square, BE = EL = LT = TB
∠B, ∠E, ∠L, ∠T are right angles.
BL = ET and BL is perpendicular ET
OB = OL and OE = OT.

29. In a square the diagonals.
(i) bisect one another (square
being a parallelogram)
(ii) are of equal length (square
being a rectangle) and
(iii) are perpendicular to one
another.
Hence, we get the following
property.
Property: The diagonals of a
square are perpendicular
bisectors of each other.