This document proposes a technique called Differential Distributed Space-Time Coding OFDM (D-DSTC OFDM) to address synchronization issues in asynchronous cooperative relay networks. It discusses how conventional distributed space-time coding suffers from inter-symbol interference due to relay synchronization errors. The proposed D-DSTC OFDM approach uses differential encoding, circular time reversal, and OFDM modulation to eliminate the need for channel state information or strict relay synchronization. Simulation results show the BER performance of D-DSTC OFDM degrades gracefully with increasing synchronization errors, outperforming coherent detection schemes. The key advantages and limitations of the D-DSTC OFDM approach are summarized.

1. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Asynchronous Differential Distributed Space-Time
Coding
M. R. Avendi
Department of Electrical Engineering & Computer Science
University of California, Irvine
Feb., 2014
1

2. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Outline
1 Introduction
2 D-DSTC
3 OFDM Systems
4 D-DSTC OFDM
5 Summary
2

3. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Cooperative Communications
Phase I: Source transmits, Relays listen
Phase II: Relays re-broadcast their received signal to
Destination
Virtual antenna array, improving diversity
q1
q2
qR
g1
g2
gR
Source
Destination
Relay 1
Relay 2
Relay R
3

4. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Relay Strategies
Repetition-based
Phase I Phase II
Source broadcasts Relay 1 forwards Relay 2 forwards Relay i forwards Relay R forwards
Time
Distributed space-time based
Phase I Phase II
Source broadcasts Relays forwards simultaneously
Time
Which one simpler to implement?
Which one bandwidth efficient?
4

5. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
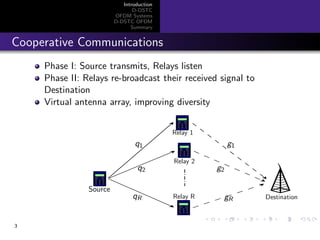
System Model
All channels are Rayleigh flat-fading
Phase I: Source transmits [s1, s2], (differential encoded)
Relays receive [x11, x12] and [x21, x22]
Phase II: Relays re-transmit [x11, x12] and [−x∗
22, x∗
21]
[s1, s2]
[x11, x12]
[−x∗
22, x∗
21]
[y1, y2]
q1
q2
g1
g2Source
Destination
Relay 1
Relay 2
5

6. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Synchronized Relay Networks
Perfect relays synchronization
y1 = g1x11 − g2x∗
22 + n1
y2 = g1x12 + g2x∗
21 + n2
y1
y2
= A P0
s1 −s∗
2
s2 s∗
1
q1g1
q∗
2g2
+
w1
w2
(1)
RX signal from Relay 1
RX signal from Relay 2
Block k
x11 x12
−x∗
22 x∗
21
6

7. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Asynchronous Relay Networks
What causes synchronization error?
– Relays at different distances from Destination
– Different processing time at relays
Relay 2 is late, 0 ≤ τ ≤ Ts, α = f (τ), β = f (Ts − τ)
y1 = g1x11 − αg2x∗
22 + βg2x∗
21
(k−1)
+ n1
y2 = g1x12 + αg2x∗
21 − βg2x∗
22 + n2
y1
y2
= A P0
s1 −s∗
2
s2 s∗
1
q1g1
αq∗
2g2
+ ISI +
w1
w2
(2)
Block (k)Block (k − 1)
τ
x11 x12
−x∗
22 x∗
21
x11 x12
−x∗
22 x∗
21
7

8. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Asynchronous Relay Networks
What causes synchronization error?
– Relays at different distances from Destination
– Different processing time at relays
Relay 2 is late, 0 ≤ τ ≤ Ts, α = f (τ), β = f (Ts − τ)
y1 = g1x11 − αg2x∗
22 + βg2x∗
21
(k−1)
+ n1
y2 = g1x12 + αg2x∗
21 − βg2x∗
22 + n2
y1
y2
= A P0
s1 −s∗
2
s2 s∗
1
q1g1
αq∗
2g2
+ ISI +
w1
w2
(2)
Block (k)Block (k − 1)
τ
x11 x12
−x∗
22 x∗
21
x11 x12
−x∗
22 x∗
21
7

9. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Asynchronous Relay Networks
Effect of synchronization error on conventional decoder (CDD)
0 5 10 15 20 25 30
10
−4
10
−3
10
−2
10
−1
10
0
CDD, τ=0
CDD, τ=0.2 Ts
CDD, τ=0.4 T
s
CDD, τ=0.6 T
s
CDD, τ=0.3 T
s
P/N0 (dB)
BER
Figure: BER of D-DSTC using BPSK at various synchronization
errors τ8

10. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
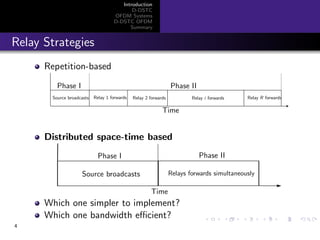
Frequency Selective Channels
Flat-fading channel, one tap filter h[k] = h0:
y[k] = h0x[k] + n[k]
Frequency selective channel, multiple taps filter:
h[k] =
L−1
l=0
hl δ[k − l]
y[k] = x ∗ h =
L
l=0
hl x[k − l] + n[k]
Inter Symbol Interference (ISI)
Orthogonal frequency-division multiplexing (OFDM)
9

11. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Point-to-Point OFDM Structure
x = [x1, · · · , xN ], y = [y1, · · · , yN]
yn = Hnxn + nn, n = 1, · · · , N
bits x
ˆx
Add
Remove
Cyclic Prefix
Cyclic Prefix
Modulation
Detection
X Xcp
ISI Channel
YcpYy
DFT
IDFT
Frequency diversity can be achieved by using channel coding
What are drawbacks of OFDM?
10

12. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
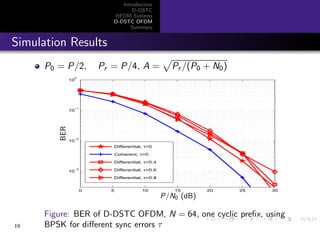
Simulation Results
5 10 15 20 25 30
10
−4
10
−3
10
−2
10
−1
SNR per bit,[dB]
biterrorprobability
Ncp=0
Ncp=2
Ncp=4
Ncp=6
Ncp=8
theory
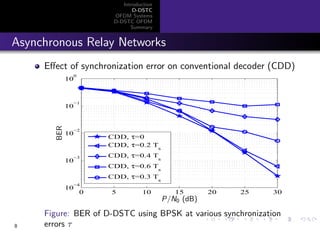
Figure: BER of OFDM system over a frequency-selective channel with
four taps, N = 128, using QPSK for different values of cyclic prefix
11

13. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Differential OFDM
v = [v1, · · · , vN ], x(k) = [x1, · · · , xN]
Differential Encoding: x
(k)
n = vnx
(k−1)
n , n = 1, · · · , N
Decoding: y
(k)
n = vny
(k−1)
n + wn, n = 1, · · · , N
Requires constant channel over two OFDM blocks, i.e., 2N
symbols
3 dB performance loss compared with coherent detection
12

14. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Simulation Results
5 10 15 20 25
10
−3
10
−2
10
−1
SNR
BER
Differential OFDM
Coherent OFDM
Figure: BER of Differential and Coherent OFDM system over a
frequency-selective channel with four taps, N = 128, using QPSK
13

15. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
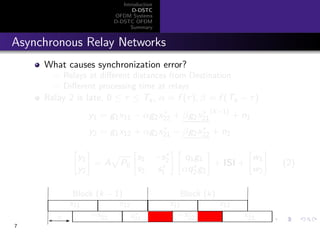
Asynchronous vs. Frequency Selectivity
Relay 2 is late:
y1 = g1x11 − αg2x∗
22 + βg2x∗
21
(k−1)
+ n1
y2 = g1x12 + αg2x∗
21 − βg2x∗
22 + n2
Relay 1-Destination channel: flat-fading, g1
Relay 2-Destination channel: can be assumed as frequency
selective, [αg2, βg2]
What is the difference between [αg2, βg2] and an actual
frequency-selective channel?
Block (k)Block (k − 1)
τ
x11 x12
−x∗
22 x∗
21
x11 x12
−x∗
22 x∗
21
14

16. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Differential Distributed Space-Time Coding OFDM
(D-DSTC OFDM)
Data symbols:
v1 = [v1(1), · · · , v1(N)], v2 = [v2(1), · · · , v2(N)]
Construct space-time matrices:
V(k) =
v1(k) −v∗
2 (k)
v2(k) v∗
1 (k)
, k = 1, · · · , N
Encode differentially: s(k) = V(k)s(k−1) =
s
(k)
1
s
(k)
2
Collect symbols:
s1 = [s1(1), · · · , s1(N)], s2 = [s2(1), · · · , s2(N)]
S1 = IDFT(s1), S2 = IDFT(s∗
2)
15

17. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
D-DSTC OFDM continue
Phase I: Source transmits [S1, S2]
Relays receive [X11, X12] and [X21, X22]
Phase II: Relays re-transmit [X11, ctr(X∗
12)] and
[−X22, ctr(X∗
21)]
[S1, S2]
[X11, ctr(X∗
12)]
[−X22, ctr(X∗
21)]
[Y1, Y2]
q1
q2
g1
g2Source
Destination
Relay 1
Relay 2
16

18. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
D-DSTC OFDM continue
Circular Time-Reversal: ctr(X) = [X(1), X(N), · · · , X(2)]
x
IDFT
−−−→ X
∗
−→ X∗ ctr
−→ ˜X
DFT
−−−→ x∗
At Destination: Remove Cyclic Prefix, apply DFT
y1 = [y1(1), · · · , y1(N)], y2 = [y2(1), · · · , y2(N)]
y(k)
=
y1(k)
y2(k)
= A P0
s1(k) −s∗
2 (k)
s2(k) s∗
1 (k)
H1
H2
+
W1
W2
,
k = 1, · · · , N
Differential decoding: y(k) = V(k)y(k−1) + ˜w(k)
17

19. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
D-DSTC OFDM: Pros and Cons
No channel information required
No delay between relays required
Higher delays: cyclic prefix
Complexity similar to OFDM, symbol-by-symbol decoding
Channels have to be static over three OFDM blocks=6N
Destination have to wait four OFDM blocks=8N before start
decoding
18

20. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
D-DSTC OFDM: Pros and Cons
No channel information required
No delay between relays required
Higher delays: cyclic prefix
Complexity similar to OFDM, symbol-by-symbol decoding
Channels have to be static over three OFDM blocks=6N
Destination have to wait four OFDM blocks=8N before start
decoding
18

21. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Simulation Results
P0 = P/2, Pr = P/4, A = Pr /(P0 + N0)
0 5 10 15 20 25 30
10
−3
10
−2
10
−1
10
0
Differential, τ=0
Coherent, τ=0
Differential, τ=0.4
Differential, τ=0.6
Differential, τ=0.8
P/N0 (dB)
BER
Figure: BER of D-DSTC OFDM, N = 64, one cyclic prefix, using
BPSK for different sync errors τ19

22. Introduction
D-DSTC
OFDM Systems
D-DSTC OFDM
Summary
Summary
Asynchronous problem in distributed space-time coding
OFDM approach
Differential encoding and decoding
No channel or delay requirement
Thank You!
20