The document presents a system model and problem formulation for user scheduling in massive MIMO OFDMA systems with hybrid analog-digital beamforming. The system considers a base station with N antennas but only Na < N RF chains serving multiple single-antenna mobile stations. The objective is to maximize the overall data rate by scheduling Kt mobile stations across subcarriers, subject to a per-subcarrier power constraint. For a single subcarrier, the problem is formulated as maximizing the sum rate of K scheduled users under a total power constraint, assuming Na = K RF chains. Two approaches are discussed: directly constraining the analog beamforming matrix or exploiting the solution from a digital scheduler using a clever decomposition method.

1. User Scheduling for Massive MIMO OFDMA
Systems with Hybrid Analog-Digital Beamforming
Tadilo Endeshaw Bogale
Institute National de la Recherche (INRS), Canada
June 9, 2015, (ICC 2015)

2. Presentation outline
Presentation outline
1 Introduction
Scenario and Objective
System Model and Problem Formulation
2 Proposed Solution
3 Performance Analysis
4 Simulation Results
5 Conclusions
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 2 / 11

3. Introduction Scenario and Objective
System Scenario and Objective
BS
a1 · · · aM
MS1
MS2
MSKt
h
1
h2
hKt
...
System Scenario
MS1, MS2, MSKt
are decentralized in space
Downlink Communications
⇒ Downlink Multiuser system
MS1, MS2, MSKt
have single antennas
⇒ Downlink Multiuser MISO system
BS has N antennas but Na < N RF chains
⇒ BS use hybrid analog-digital architecture
(To get better performance (Clear later!))
Channel between Tx and Rx is Freq. Selective
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 3 / 11

4. Introduction Scenario and Objective
System Scenario and Objective
BS
a1 · · · aM
MS1
MS2
MSKt
h
1
h2
hKt
...
System Scenario
MS1, MS2, MSKt
are decentralized in space
Downlink Communications
⇒ Downlink Multiuser system
MS1, MS2, MSKt
have single antennas
⇒ Downlink Multiuser MISO system
BS has N antennas but Na < N RF chains
⇒ BS use hybrid analog-digital architecture
(To get better performance (Clear later!))
Channel between Tx and Rx is Freq. Selective
Objective
Schedule Kt MSs (Ki, ∀i)
To maximize the Overall Data Rate
S.t. Per sub-carrier Power constraint
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 3 / 11

5. Introduction System Model and Problem Formulation
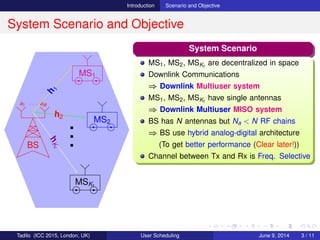
System Model and Problem Formulation
Source Tx (Digital part) RF Chain Tx (Analog part)
Freq. Dom.
data source
D(1,:)
D(2,:)
D(K,:)
•••
Freq. Dom.
BF
1
2
Na
•••
IFFT (row)
& add CP
1
2
Na
•••
RF1
analog
RF2
analog
RFNa
analog
•••
Analog
BF
Analog
BF
Analog
BF
•••
N
N
N
•••
2
2
2
1
1
1
1
2
N
•••
•••
•••
•••
•••
•••
H
1 Discard CP
& take FFT
ˆdi1 Decode
ˆd11, · · · , ˆdNf 1
2 Discard CP
& take FFT
ˆdi2 Decode
ˆd12, · · · , ˆdNf 2
K Discard CP
& take FFT
ˆdiK Decode
ˆd1K, · · · , ˆdNf K
•••
d1, · · · , dNf
B1, · · · , BNf A
ˆdik = hH
ikABidi + nik
FH F
Problem Formulation
max
A,Bi
Nf
i=1
Ki
k=1
log(1 + γik )
Nf
i=1
f(ABi)
s.t tr{BH
i AH
ABi} ≤ Pi
Ki: Users served by sub-carrier i
B = [B1, B2, · · · , BNf
], Bi ∈ CNa×Si
γik : SINR of ith sub-carrier kth user
A ∈ CNa×N: Realized using PSs only
(Expected to be more constrained!)
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 4 / 11

6. Introduction System Model and Problem Formulation
System Model and Problem Formulation
Source Tx (Digital part) RF Chain Tx (Analog part)
Freq. Dom.
data source
D(1,:)
D(2,:)
D(K,:)
•••
Freq. Dom.
BF
1
2
Na
•••
IFFT (row)
& add CP
1
2
Na
•••
RF1
analog
RF2
analog
RFNa
analog
•••
Analog
BF
Analog
BF
Analog
BF
•••
N
N
N
•••
2
2
2
1
1
1
1
2
N
•••
•••
•••
•••
•••
•••
H
1 Discard CP
& take FFT
ˆdi1 Decode
ˆd11, · · · , ˆdNf 1
2 Discard CP
& take FFT
ˆdi2 Decode
ˆd12, · · · , ˆdNf 2
K Discard CP
& take FFT
ˆdiK Decode
ˆd1K, · · · , ˆdNf K
•••
d1, · · · , dNf
B1, · · · , BNf A
ˆdik = hH
ikABidi + nik
FH F
Problem Formulation
max
A,Bi
Nf
i=1
Ki
k=1
log(1 + γik )
Nf
i=1
f(ABi)
s.t tr{BH
i AH
ABi} ≤ Pi
Ki: Users served by sub-carrier i
B = [B1, B2, · · · , BNf
], Bi ∈ CNa×Si
γik : SINR of ith sub-carrier kth user
A ∈ CNa×N: Realized using PSs only
(Expected to be more constrained!)
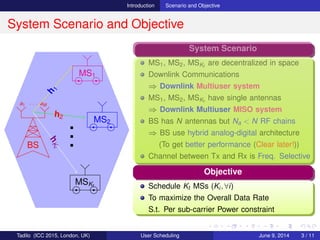
For one Sub-carrier (Flat fading)
max
A,B
K
k=1
log(1 + γk )
s.t tr{BH
AH
AB} ≤ Pmax
Kt : Total number of users
K: Scheduled users
Assume that we have Na = K RF chains
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 4 / 11

7. Introduction System Model and Problem Formulation
System Model and Problem Formulation
Source Tx (Digital part) RF Chain Tx (Analog part)
Freq. Dom.
data source
D(1,:)
D(2,:)
D(K,:)
•••
Freq. Dom.
BF
1
2
Na
•••
IFFT (row)
& add CP
1
2
Na
•••
RF1
analog
RF2
analog
RFNa
analog
•••
Analog
BF
Analog
BF
Analog
BF
•••
N
N
N
•••
2
2
2
1
1
1
1
2
N
•••
•••
•••
•••
•••
•••
H
1 Discard CP
& take FFT
ˆdi1 Decode
ˆd11, · · · , ˆdNf 1
2 Discard CP
& take FFT
ˆdi2 Decode
ˆd12, · · · , ˆdNf 2
K Discard CP
& take FFT
ˆdiK Decode
ˆd1K, · · · , ˆdNf K
•••
d1, · · · , dNf
B1, · · · , BNf A
ˆdik = hH
ikABidi + nik
FH F
Problem Formulation
max
A,Bi
Nf
i=1
Ki
k=1
log(1 + γik )
Nf
i=1
f(ABi)
s.t tr{BH
i AH
ABi} ≤ Pi
Ki: Users served by sub-carrier i
B = [B1, B2, · · · , BNf
], Bi ∈ CNa×Si
γik : SINR of ith sub-carrier kth user
A ∈ CNa×N: Realized using PSs only
(Expected to be more constrained!)
For one Sub-carrier (Flat fading)
max
A,B
K
k=1
log(1 + γk )
s.t tr{BH
AH
AB} ≤ Pmax
Kt : Total number of users
K: Scheduled users
Assume that we have Na = K RF chains
First Possibility
max
A,B
K
k=1
log(1 + γk )
s.t tr{BH
AH
AB} ≤ Pmax , |Aij|2
= 1
Disadvantage:
How far from digital scheduler which is
an optimal approach?
(Not clearly known for general channel)
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 4 / 11

8. Introduction System Model and Problem Formulation
System Model and Problem Formulation
Source Tx (Digital part) RF Chain Tx (Analog part)
Freq. Dom.
data source
D(1,:)
D(2,:)
D(K,:)
•••
Freq. Dom.
BF
1
2
Na
•••
IFFT (row)
& add CP
1
2
Na
•••
RF1
analog
RF2
analog
RFNa
analog
•••
Analog
BF
Analog
BF
Analog
BF
•••
N
N
N
•••
2
2
2
1
1
1
1
2
N
•••
•••
•••
•••
•••
•••
H
1 Discard CP
& take FFT
ˆdi1 Decode
ˆd11, · · · , ˆdNf 1
2 Discard CP
& take FFT
ˆdi2 Decode
ˆd12, · · · , ˆdNf 2
K Discard CP
& take FFT
ˆdiK Decode
ˆd1K, · · · , ˆdNf K
•••
d1, · · · , dNf
B1, · · · , BNf A
ˆdik = hH
ikABidi + nik
FH F
Problem Formulation
max
A,Bi
Nf
i=1
Ki
k=1
log(1 + γik )
Nf
i=1
f(ABi)
s.t tr{BH
i AH
ABi} ≤ Pi
Ki: Users served by sub-carrier i
B = [B1, B2, · · · , BNf
], Bi ∈ CNa×Si
γik : SINR of ith sub-carrier kth user
A ∈ CNa×N: Realized using PSs only
(Expected to be more constrained!)
For one Sub-carrier (Flat fading)
max
A,B
K
k=1
log(1 + γk )
s.t tr{BH
AH
AB} ≤ Pmax
Kt : Total number of users
K: Scheduled users
Assume that we have Na = K RF chains
First Possibility
max
A,B
K
k=1
log(1 + γk )
s.t tr{BH
AH
AB} ≤ Pmax , |Aij|2
= 1
Disadvantage:
How far from digital scheduler which is
an optimal approach?
(Not clearly known for general channel)
Second Possibility
max
Bd
K
k=1
log(1 + γk )
s.t tr{(Bd
)H
Bd
} ≤ Pmax
Exploit the solution of digital scheduler:
Fact: rank(Bd ) ≤ K for any scheduler
Clever Method [1]: Bd = UD, U ∈ CN×2K ,
D ∈ R2K×K , D = blkdiag matrix
∴ 2K RF chain: No performance loss
VIP: No need to constrain |Aij|2 = 1
REREFENCES
1 X. Zhang, A. F. Molisch, and S-Y. Kung, ”Variable-phase-shift-based RF-Baseband codesign for MIMO antenna
selection” IEEE Trans. Signal Process., vol. 53, no. 11, pp. 4091 - 4103, Nov. 2005.
2 T. E. Bogale, L. Le, A. Haghighat, and L. Vandendorpe ”On the Number of RF Chains and Phase Shifters, and
Scheduling Design with Hybrid Analog-Digital Beamforming,” IEEE Trans. (Submitted),
http://arxiv.org/abs/1410.2609.
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 4 / 11

9. Introduction System Model and Problem Formulation
System Model and Problem Formulation
Source Tx (Digital part) RF Chain Tx (Analog part)
Freq. Dom.
data source
D(1,:)
D(2,:)
D(K,:)
•••
Freq. Dom.
BF
1
2
Na
•••
IFFT (row)
& add CP
1
2
Na
•••
RF1
analog
RF2
analog
RFNa
analog
•••
Analog
BF
Analog
BF
Analog
BF
•••
N
N
N
•••
2
2
2
1
1
1
1
2
N
•••
•••
•••
•••
•••
•••
H
1 Discard CP
& take FFT
ˆdi1 Decode
ˆd11, · · · , ˆdNf 1
2 Discard CP
& take FFT
ˆdi2 Decode
ˆd12, · · · , ˆdNf 2
K Discard CP
& take FFT
ˆdiK Decode
ˆd1K, · · · , ˆdNf K
•••
d1, · · · , dNf
B1, · · · , BNf A
ˆdik = hH
ikABidi + nik
FH F
Problem Formulation
max
A,Bi
Nf
i=1
Ki
k=1
log(1 + γik )
Nf
i=1
f(ABi)
s.t tr{BH
i AH
ABi} ≤ Pi
Ki: Users served by sub-carrier i
B = [B1, B2, · · · , BNf
], Bi ∈ CNa×Si
γik : SINR of ith sub-carrier kth user
A ∈ CNa×N: Realized using PSs only
(Expected to be more constrained!)
For one Sub-carrier (Flat fading)
max
A,B
K
k=1
log(1 + γk )
s.t tr{BH
AH
AB} ≤ Pmax
Kt : Total number of users
K: Scheduled users
Assume that we have Na = K RF chains
First Possibility
max
A,B
K
k=1
log(1 + γk )
s.t tr{BH
AH
AB} ≤ Pmax , |Aij|2
= 1
Disadvantage:
How far from digital scheduler which is
an optimal approach?
(Not clearly known for general channel)
Second Possibility
max
Bd
K
k=1
log(1 + γk )
s.t tr{(Bd
)H
Bd
} ≤ Pmax
Exploit the solution of digital scheduler:
Fact: rank(Bd ) ≤ K for any scheduler
Clever Method [1]: Bd = UD, U ∈ CN×2K ,
D ∈ R2K×K , D = blkdiag matrix
∴ 2K RF chain: No performance loss
VIP: No need to constrain |Aij|2 = 1
Observations
U and D are not unique
Question: Can we make U and D unique
and reduce RF chain < 2K
Answer: Yes, by employing [2]
x = ej cos−1( x
2
)
+ e−j cos−1( x
2
)
, for −2 ≤ x ≤ 2
⇒ Bd = ˜U ˜D, with | ˜Uij|2 = 1 and
˜D = blkdiag two consecutive diag elements
are the same
⇒ K RF chain is enough [2]
∴ Scheduling without |Aij|2 = 1 (Simpler)
REREFENCES
1 X. Zhang, A. F. Molisch, and S-Y. Kung, ”Variable-phase-shift-based RF-Baseband codesign for MIMO antenna
selection” IEEE Trans. Signal Process., vol. 53, no. 11, pp. 4091 - 4103, Nov. 2005.
2 T. E. Bogale, L. Le, A. Haghighat, and L. Vandendorpe ”On the Number of RF Chains and Phase Shifters, and
Scheduling Design with Hybrid Analog-Digital Beamforming,” IEEE Trans. (Submitted),
http://arxiv.org/abs/1410.2609.
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 4 / 11

10. Introduction System Model and Problem Formulation
System Model and Problem Formulation
Source Tx (Digital part) RF Chain Tx (Analog part)
Freq. Dom.
data source
D(1,:)
D(2,:)
D(K,:)
•••
Freq. Dom.
BF
1
2
Na
•••
IFFT (row)
& add CP
1
2
Na
•••
RF1
analog
RF2
analog
RFNa
analog
•••
Analog
BF
Analog
BF
Analog
BF
•••
N
N
N
•••
2
2
2
1
1
1
1
2
N
•••
•••
•••
•••
•••
•••
H
1 Discard CP
& take FFT
ˆdi1 Decode
ˆd11, · · · , ˆdNf 1
2 Discard CP
& take FFT
ˆdi2 Decode
ˆd12, · · · , ˆdNf 2
K Discard CP
& take FFT
ˆdiK Decode
ˆd1K, · · · , ˆdNf K
•••
d1, · · · , dNf
B1, · · · , BNf A
ˆdik = hH
ikABidi + nik
FH F
Problem Formulation
max
A,Bi
Nf
i=1
Ki
k=1
log(1 + γik )
Nf
i=1
f(ABi)
s.t tr{BH
i AH
ABi} ≤ Pi
Ki: Users served by sub-carrier i
B = [B1, B2, · · · , BNf
], Bi ∈ CNa×Si
γik : SINR of ith sub-carrier kth user
A ∈ CNa×N: Realized using PSs only
(Expected to be more constrained!)
For one Sub-carrier (Flat fading)
max
A,B
K
k=1
log(1 + γk )
s.t tr{BH
AH
AB} ≤ Pmax
Kt : Total number of users
K: Scheduled users
Assume that we have Na = K RF chains
First Possibility
max
A,B
K
k=1
log(1 + γk )
s.t tr{BH
AH
AB} ≤ Pmax , |Aij|2
= 1
Disadvantage:
How far from digital scheduler which is
an optimal approach?
(Not clearly known for general channel)
Second Possibility
max
Bd
K
k=1
log(1 + γk )
s.t tr{(Bd
)H
Bd
} ≤ Pmax
Exploit the solution of digital scheduler:
Fact: rank(Bd ) ≤ K for any scheduler
Clever Method [1]: Bd = UD, U ∈ CN×2K ,
D ∈ R2K×K , D = blkdiag matrix
∴ 2K RF chain: No performance loss
VIP: No need to constrain |Aij|2 = 1
Observations
U and D are not unique
Question: Can we make U and D unique
and reduce RF chain < 2K
Answer: Yes, by employing [2]
x = ej cos−1( x
2
)
+ e−j cos−1( x
2
)
, for −2 ≤ x ≤ 2
⇒ Bd = ˜U ˜D, with | ˜Uij|2 = 1 and
˜D = blkdiag two consecutive diag elements
are the same
⇒ K RF chain is enough [2]
∴ Scheduling without |Aij|2 = 1 (Simpler)
Problem Formulation
max
A,Bi
Nf
i=1
Ki
k=1
log(1 + γik )
Nf
i=1
f(ABi)
s.t tr{BH
i AH
ABi} ≤ Pi
Ki: Users served by sub-carrier i
B = [B1, B2, · · · , BNf
], Bi ∈ CNa×Si
γik : SINR of ith sub-carrier kth user
A ∈ CNa×N: Realized using PSs only
(Expected to be more constrained!)
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 4 / 11

11. Proposed Solution
Proposed Solution
Input: Hki , Ki , Pi , Na
Solve Relaxed Problem
rank( ¯B) ≤ Na?
Get A, Bi : From SVD( ¯B)
FINISH
Yes
Determine A
Given A: Optimize Bi
FINISH
No
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 5 / 11

12. Proposed Solution
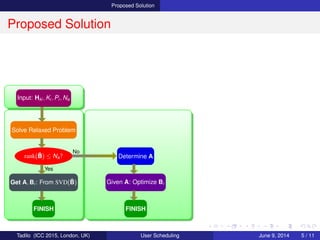
Proposed Solution
Input: Hki , Ki , Pi , Na
Solve Relaxed Problem
rank( ¯B) ≤ Na?
Get A, Bi : From SVD( ¯B)
FINISH
Yes
Determine A
Given A: Optimize Bi
FINISH
No
Relaxed Problem
Assume the system as if it is DB
(i.e., implicitly uses Na = N and A = I)
⇒ Scheduling independently for each SC
max
¯Bi
Ki
k=1
log(1 + ¯γik ) f( ¯Bi),
s.t tr{ ¯BH
i
¯Bi} ≤ Pi
Gready based Scheduler
Zero forcing (ZF) beamforming
Set ¯B = [ ¯B1, ¯B2, · · · , ¯BNf
]
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 5 / 11

13. Proposed Solution
Proposed Solution
Input: Hki , Ki , Pi , Na
Solve Relaxed Problem
rank( ¯B) ≤ Na?
Get A, Bi : From SVD( ¯B)
FINISH
Yes
Determine A
Given A: Optimize Bi
FINISH
No
Relaxed Problem
Assume the system as if it is DB
(i.e., implicitly uses Na = N and A = I)
⇒ Scheduling independently for each SC
max
¯Bi
Ki
k=1
log(1 + ¯γik ) f( ¯Bi),
s.t tr{ ¯BH
i
¯Bi} ≤ Pi
Gready based Scheduler
Zero forcing (ZF) beamforming
Set ¯B = [ ¯B1, ¯B2, · · · , ¯BNf
]
Determination of A
Sort f( ¯B1) ≥ f( ¯B2) ≥, · · · , ≥ f( ¯BNf
)
Get ˜Bd = [ ¯B1, ¯B2, · · · , ¯B˜S
]
˜S: Min No of SC with rank( ˜B) ≥ Na
Compute SVD( ˜B) = UΛVH
Λ arranged in decreasing order.
Set A: First Na columns of U
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 5 / 11

14. Proposed Solution
Proposed Solution
Input: Hki , Ki , Pi , Na
Solve Relaxed Problem
rank( ¯B) ≤ Na?
Get A, Bi : From SVD( ¯B)
FINISH
Yes
Determine A
Given A: Optimize Bi
FINISH
No
Relaxed Problem
Assume the system as if it is DB
(i.e., implicitly uses Na = N and A = I)
⇒ Scheduling independently for each SC
max
¯Bi
Ki
k=1
log(1 + ¯γik ) f( ¯Bi),
s.t tr{ ¯BH
i
¯Bi} ≤ Pi
Gready based Scheduler
Zero forcing (ZF) beamforming
Set ¯B = [ ¯B1, ¯B2, · · · , ¯BNf
]
Determination of A
Sort f( ¯B1) ≥ f( ¯B2) ≥, · · · , ≥ f( ¯BNf
)
Get ˜Bd = [ ¯B1, ¯B2, · · · , ¯B˜S
]
˜S: Min No of SC with rank( ˜B) ≥ Na
Compute SVD( ˜B) = UΛVH
Λ arranged in decreasing order.
Set A: First Na columns of U
Optimize Bi for fixed A
For fixed A: Each sub-carrier can
perform scheduling independently
max
Bi
Ki
k=1
log(1 + γik )
Nf
i=1
f(Bi)
s.t tr{BH
i AH
ABi} ≤ Pi
Gready based Scheduler
Zero forcing (ZF) beamforming
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 5 / 11

15. Proposed Solution
Proposed Solution
Input: Hki , Ki , Pi , Na
Solve Relaxed Problem
rank( ¯B) ≤ Na?
Get A, Bi : From SVD( ¯B)
FINISH
Yes
Determine A
Given A: Optimize Bi
FINISH
No
Determination of A
Sort f( ¯B1) ≥ f( ¯B2) ≥, · · · , ≥ f( ¯BNf
)
Get ˜Bd = [ ¯B1, ¯B2, · · · , ¯B˜S
]
˜S: Min No of SC with rank( ˜B) ≥ Na
Compute SVD( ˜B) = UΛVH
Λ arranged in decreasing order.
Set A: First Na columns of U
Relaxed Problem
Assume the system as if it is DB
(i.e., implicitly uses Na = N and A = I)
⇒ Scheduling independently for each SC
max
¯Bi
Ki
k=1
log(1 + ¯γik ) f( ¯Bi),
s.t tr{ ¯BH
i
¯Bi} ≤ Pi
Gready based Scheduler
Zero forcing (ZF) beamforming
Set ¯B = [ ¯B1, ¯B2, · · · , ¯BNf
]
Optimize Bi for fixed A
For fixed A: Each sub-carrier can
perform scheduling independently
max
Bi
Ki
k=1
log(1 + γik )
Nf
i=1
f(Bi)
s.t tr{BH
i AH
ABi} ≤ Pi
Gready based Scheduler
Zero forcing (ZF) beamforming
Conclusions
A user may be scheduled
in one (more) sub-carriers
Proposed solution may
not be global optimal
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 5 / 11

16. Performance Analysis
Performance Analysis
Approaches
Three approaches examined:
Antenna Selection Beamforming (ASB):
Implicitly assumes A = IN×Na
Proposed Hybrid Beamforming (HB)
Digital Beamforming (DB):
Assumes N RF chains and A = IN
Intuitive expectation
P(ASB) ≤ P(HB) ≤ P(DB)
To what extent?
In what scenario?
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 6 / 11

17. Performance Analysis
Performance Analysis
Approaches
Three approaches examined:
Antenna Selection Beamforming (ASB):
Implicitly assumes A = IN×Na
Proposed Hybrid Beamforming (HB)
Digital Beamforming (DB):
Assumes N RF chains and A = IN
Intuitive expectation
P(ASB) ≤ P(HB) ≤ P(DB)
To what extent?
In what scenario?
Performance: Rayleigh Channel
Rayleigh Fading Channel:
Lemma 1: ZF beamforming, Rayleigh fading ˜hH
k and large Kt ,
we have
RHB
i ≥ RASB
i when KHB
i = KASB
i , and
RHB
i = RDB
i when KHB
i = KDB
i
KHB
i = KDB
i may not hold, ⇒ Average performance makes sense
Theorem 1: ZF beamforming with Pi = P, Ki = K and Rayleigh
fading channel ˜hH
k , we have
E{RASB
} ≤ KNf log2 1 +
P
K
E{χNa−K+1
max (Kg)}
E{RDB
} ≤ KNf log2 1 +
P
K
E{χN−K+1
max (Kg)}
E{RHB
} ≤ K ˜S log2 1 +
P
K
E{χN−K+1
max (Ks)}
+ K(Nf − ˜S) log2 1 +
P
K
E{χNa−K+1
max (Kg)}
where E{χM
max (L)}: Max. of L independent χ2 each with M DOF,
˜S ≥ 1, Kg = Kt
K and Ks = Kt Nf
KNa
Simulation: Bound is tight
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 6 / 11

18. Performance Analysis
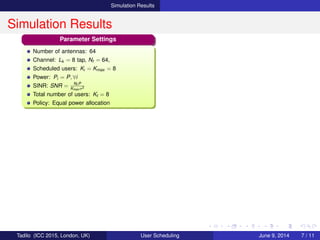
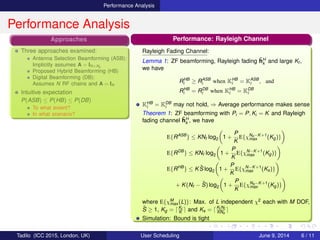
Performance Analysis
Approaches
Three approaches examined:
Antenna Selection Beamforming (ASB):
Implicitly assumes A = IN×Na
Proposed Hybrid Beamforming (HB)
Digital Beamforming (DB):
Assumes N RF chains and A = IN
Intuitive expectation
P(ASB) ≤ P(HB) ≤ P(DB)
To what extent?
In what scenario?
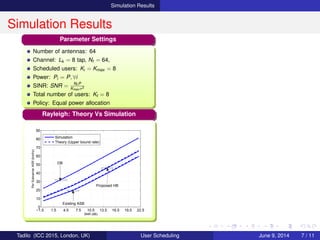
Performance: Rayleigh Channel
Rayleigh Fading Channel:
Lemma 1: ZF beamforming, Rayleigh fading ˜hH
k and large Kt ,
we have
RHB
i ≥ RASB
i when KHB
i = KASB
i , and
RHB
i = RDB
i when KHB
i = KDB
i
KHB
i = KDB
i may not hold, ⇒ Average performance makes sense
Theorem 1: ZF beamforming with Pi = P, Ki = K and Rayleigh
fading channel ˜hH
k , we have
E{RASB
} ≤ KNf log2 1 +
P
K
E{χNa−K+1
max (Kg)}
E{RDB
} ≤ KNf log2 1 +
P
K
E{χN−K+1
max (Kg)}
E{RHB
} ≤ K ˜S log2 1 +
P
K
E{χN−K+1
max (Ks)}
+ K(Nf − ˜S) log2 1 +
P
K
E{χNa−K+1
max (Kg)}
where E{χM
max (L)}: Max. of L independent χ2 each with M DOF,
˜S ≥ 1, Kg = Kt
K and Ks = Kt Nf
KNa
Simulation: Bound is tight
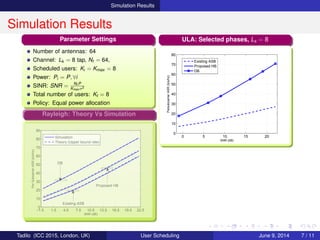
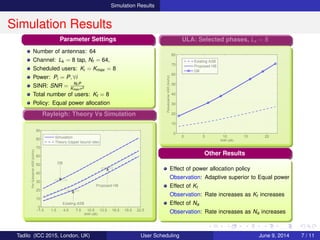
Performance: ULA Channel
Rayleigh:
DB Scheduler: Likely chooses users
close to orthogonal each other
Proposed HB achieves lower sum rate
(Mainly due to rank(H) > Na)
∴ if rank(H) ≤ Na then RHB
i ≈ RDB
i
ULA: Condition rank(H) Na exists
Lemma 2: When ˜d = λ
2 and the AOD of
the Kt users satisfy sin (θkm) ∈
n sin (θ)[− 1
2N , 1
2N ], n = 1, 2, · · · , Na,
where θ is an arbitrary angle,
KHB
i = KDB
i and RHB
i = RDB
i , ∀i
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 6 / 11

19. Simulation Results
Simulation Results
Parameter Settings
Number of antennas: 64
Channel: Lk = 8 tap, Nf = 64,
Scheduled users: Ki = Kmax = 8
Power: Pi = P, ∀i
SINR: SNR = Nf P
Kmax σ2
Total number of users: Kt = 8
Policy: Equal power allocation
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 7 / 11

20. Simulation Results
Simulation Results
Parameter Settings
Number of antennas: 64
Channel: Lk = 8 tap, Nf = 64,
Scheduled users: Ki = Kmax = 8
Power: Pi = P, ∀i
SINR: SNR = Nf P
Kmax σ2
Total number of users: Kt = 8
Policy: Equal power allocation
Rayleigh: Theory Vs Simulation
−1.5 1.5 4.5 7.5 10.5 13.5 16.5 19.5 22.5
0
10
20
30
40
50
60
70
80
90
SNR (dB)
PerSubcarrierASR(b/s/hz)
Simulation
Theory (Upper bound rate)
DB
Existing ASB
Proposed HB
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 7 / 11

21. Simulation Results
Simulation Results
Parameter Settings
Number of antennas: 64
Channel: Lk = 8 tap, Nf = 64,
Scheduled users: Ki = Kmax = 8
Power: Pi = P, ∀i
SINR: SNR = Nf P
Kmax σ2
Total number of users: Kt = 8
Policy: Equal power allocation
Rayleigh: Theory Vs Simulation
−1.5 1.5 4.5 7.5 10.5 13.5 16.5 19.5 22.5
0
10
20
30
40
50
60
70
80
90
SNR (dB)
PerSubcarrierASR(b/s/hz)
Simulation
Theory (Upper bound rate)
DB
Existing ASB
Proposed HB
ULA: Selected phases, Ls = 8
0 5 10 15 20
0
10
20
30
40
50
60
70
80
SNR (dB)
PersubcarrierASR(b/s/hz)
Existing ASB
Proposed HB
DB
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 7 / 11

22. Simulation Results
Simulation Results
Parameter Settings
Number of antennas: 64
Channel: Lk = 8 tap, Nf = 64,
Scheduled users: Ki = Kmax = 8
Power: Pi = P, ∀i
SINR: SNR = Nf P
Kmax σ2
Total number of users: Kt = 8
Policy: Equal power allocation
Rayleigh: Theory Vs Simulation
−1.5 1.5 4.5 7.5 10.5 13.5 16.5 19.5 22.5
0
10
20
30
40
50
60
70
80
90
SNR (dB)
PerSubcarrierASR(b/s/hz)
Simulation
Theory (Upper bound rate)
DB
Existing ASB
Proposed HB
ULA: Selected phases, Ls = 8
0 5 10 15 20
0
10
20
30
40
50
60
70
80
SNR (dB)
PersubcarrierASR(b/s/hz)
Existing ASB
Proposed HB
DB
Other Results
Effect of power allocation policy
Observation: Adaptive superior to Equal power
Effect of Kt
Observation: Rate increases as Kt increases
Effect of Na
Observation: Rate increases as Na increases
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 7 / 11

23. Conclusions
Conclusions
In this work, we accomplish the following main tasks.
We propose greedy like user scheduling algorithm with hybrid
analog-digital beamforming
The proposed hybrid scheduling achieves better than antenna
selection approach
We analyze the performance of the proposed hybrid scheduling
for Rayleigh and ULA channels
Theoretical results are confirmed via extensive simulations
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 8 / 11

24. Conclusions
References I
O. E. Ayach, S. Rajagopal, S. Abu-Surra, Z. Pi, and R. W. Heath,
Spatially sparse precoding in millimeter wave MIMO systems,
IEEE Trans. Wireless Commun. 13 (2014), no. 3, 1499 – 1513.
T. E. Bogale and L. B. Le, Beamforming for multiuser massive
MIMO systems: Digital versus hybrid analog-digital, Proc. IEEE
Global Telecommun. Conf. (GLOBECOM) (Austin, Tx, USA), 10 –
12 Dec. 2014.
T. E. Bogale, L. B. Le, A. Haghighat, and L. Vandendorpe, On the
number of RF chains and phase shifters, and scheduling design
with hybrid analog-digital beamforming, IEEE Trans. Wireless
Commun. (Submitted) (2014).
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 9 / 11

25. Conclusions
References II
S. Hur, T. Kim, D. J. Love, J. V. Krogmeier, T. A. Thomas, and
A. Ghosh, Millimeter wave beamforming for wireless backhaul and
access in small cell networks, IEEE Trans. Commun. 61 (2013),
no. 10.
T. L. Marzetta, Noncooperative cellular wireless with unlimited
numbers of base station antennas, IEEE Trans. Wireless Commun.
9 (2010), no. 11, 3590 – 3600.
S. Thoen, L. Van der Perre, B. Gyselinckx, and M. Engels,
Performance analysis of combined Transmit-SC/Receive-MRC,
IEEE Trans. Commun. 49 (2001), no. 1, 5 – 8.
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 10 / 11

26. Conclusions
References III
V. Venkateswaran and A-J. V. Veen, Analog beamforming in MIMO
communications with phase shift networks and online channel
estimation, IEEE Trans. Signal Process. 58 (2010), no. 8, 4131 –
4143.
T. Yoo and A. Goldsmith, On the optimality of multiantenna
broadcast scheduling using zero-forcing beamforming, IEEE Trans.
Sel. Area. Commun. 24 (2006), no. 3, 528 – 541.
E. Zhang and C. Huang, On achieving optimal rate of digital
precoder by RF-Baseband codesign for MIMO systems, Proc.
IEEE Veh. Technol. Conf. (VTC Fall), 2014, pp. 1 – 5.
X. Zhang, A. F. Molisch, and S-Y. Kung, Variable-phase-shift-based
RF-Baseband codesign for MIMO antenna selection, IEEE Trans.
Signal Process. 53 (2005), no. 11, 4091 – 4103.
Tadilo (ICC 2015, London, UK) User Scheduling June 9, 2015, (ICC 2015) 11 / 11