This document discusses direct digital synthesis (DDS) techniques. DDS allows digitally generating waveforms by mapping a phase increment to sinusoidal outputs. Key aspects covered include: phase truncation DDS using lookup tables, dithered DDS to reduce spurs, and Taylor series expansion DDS for higher precision. Applications include digital up/down converters. Multi-channel DDS can efficiently generate multiple signals using time division multiplexing of hardware.

1. Direct Digital Synthesis
1
FPGA Signal Processing:
Direct Digital Synthesis
Santa Clara University
Dr Chris Dick
DSP Chief Architect
Xilinx
© Chris Dick 2004-2009DDS v2.1 2
Direct Digital Synthesis (DDS)
• DDS Implementation Options
– phase truncation DDS
– CORDIC
– series expansions
– phase dithered DDS
– error feed-forward
– error feed-back
n
θ(n)
Angle to
sin/cos
algorithm
n
2 ( )j n
e πθ
DDS maps a phase slope θ(n) to a (possible complex) sinusoid
DDS

2. Direct Digital Synthesis
2
© Chris Dick 2004-2009DDS v2.1 3
DDS Applications
• Digital receivers
– digital down converter (DDC)
– digital up converter (DUC)
– local oscillator generation in a digital phase locked loop
– generating an injection frequency (via an DAC) for use with an
analog mixer
– phase & frequency modulators
– frequency hopping systems
© Chris Dick 2004-2009DDS v2.1 4
Phase Truncation DDS
π/2 SINE
COSINE
LOOK-UP TABLE
2’s
COMPLE-
MENTER
2’s
COMPLE-
MENTER
N N-2 N-2
MSB (bit N-1)
2nd MSB (bit N-2)
PHASE
ACCUMULATOR
sin( )
cos( )
PHASE
INCREMENT
∆φ
Q()
( )nθ
( )n
Bθ
( )nΘ
( )n
BΘ Sin/cos
Lookup
Table
( )cos ( )nΘ
( )sin ( )nΘ
Phase increment
θ∆
sB
sB
clkf
DDS with Lookup table compression
1’s
comple-
menter
phase offset
lookup table

3. Direct Digital Synthesis
3
© Chris Dick 2004-2009DDS v2.1 5
DDS Frequency Resolution
• Accumulator width must support enough precision to span
the desired frequency resolution
Q()
( )nθ
( )n
Bθ ˆ( )n
B
θ Sin/cos
Lookup
Table
( )ˆcos ( )nθ
( )ˆsin ( )nθ
Phase increment
θ∆
sB
sB
clkf
clk
out
( )
Hz
2
B
n
f
f
θ
θ∆
=
( )
2
Frequency resolution: n
clk
B
f
f θ
∆ =
ˆ( )nθ
© Chris Dick 2004-2009DDS v2.1 6
DDS Frequency Resolution
• Example:
– if the sampling clock is 100 MHz and accumulator width is 32-
bits, the frequency resolution is ~0.02 Hz.

4. Direct Digital Synthesis
4
© Chris Dick 2004-2009DDS v2.1 7
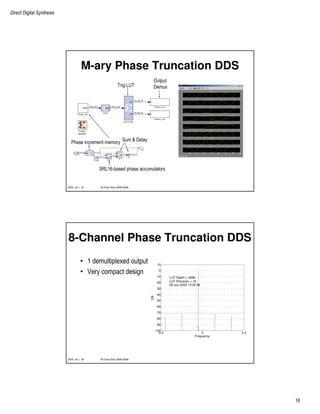
Phase Truncation DDS
0 0.1 0.2 0.3 0.4 0.5
-100
-80
-60
-40
-20
0
NORMALIZED FREQUENCY
DB
PHASE
INCREMENT
∆φ M
clk
PHASE
ACCUMULATOR
(e.g. 28-32 bits)
fout = ∆φ fclk/2N
SINE/COSINE
LOOKUP
TABLE
e.g. N = 8-16
θ(n)^
θ(n)
Q( )
N sin(θ(n))
^
cos(θ(n))^
B
B
0 20 40 60 80 100
0
0.5
1
TIME
ERROR
20 40 60 80 100
-1
0
1
TIME
AMPLITUDE
© Chris Dick 2004-2009DDS v2.1 8
DDS Noise
• The term contributing to the DDS noise
component can be calculated by examining the
effect of the phase accumulator quantizer
ˆ( ) [ ( ) ( )] ( ) ( )
ˆ( ) ( )
( ) ( )
ˆ( ) ( ) ( )
[1 ( )]
( )
DESIRED COMPONENT
UNDESIRED COMPONENT
j n j n n j n j n
j n j n
j n j n
n n n
e e e e
e e j n
e j n e
θ θ δθ θ δθ
θ θ
θ θ
θ θ δθ
δθ
δθ
+
= +
= =
≈ +
= +

5. Direct Digital Synthesis
5
© Chris Dick 2004-2009DDS v2.1 9
Dithered DDS
PHASE
INCREMENT
∆φ M
clk
PHASE
ACCUMULATOR
Q( )
fout = ∆φ fclk/2N
SINE/COSINE
LOOKUP
TABLEN
d(n)
DITHER
SIGNAL
sin(θ(n))
^
cos(θ(n))^θ(n) θ(n)^
B
B
0 0.1 0.2 0.3 0.4 0.5
-100
-80
-60
-40
-20
0
NORMALIZED FREQUENCY
DB
0 20 40 60 80 100
-1
0
1
2
TIME
ERROR
20 40 60 80 100
-1
0
1
TIME
AMPLITUDE
© Chris Dick 2004-2009DDS v2.1 10
Generating the Dither Sequence
• Generate the dither sequence using linear feedback shift
register structure

6. Direct Digital Synthesis
6
© Chris Dick 2004-2009DDS v2.1 11
0 10 20 30 40 50 60
-120
-100
-80
-60
-40
-20
0
-72 dB
-84 dB
Frequency (MHz)
dB
f
0
= 10.2MHz
Peak Spur = -84.3037dB
LUT Depth = 4096
LUT Precision = 12
PACC Precision = 32
04-Sep-2001 22:30:09
Performance: Single Tone
0 10 20 30 40 50 60
-120
-100
-80
-60
-40
-20
0
-72 dB
-84 dB
Frequency (MHz)
dB
f
0
= 10.2MHz
Peak Spur = -71.7267dB
LUT Depth = 4096
LUT Precision = 12
PACC Precision = 32
04-Sep-2001 22:22:19
Dithering Disabled Dithering Enabled
0 10.2 MHz
peak spur = -71.73 dB
LUT depth = 4096
LUT precision = 12b
PACC precision = 32b
f = 0 10.2 MHz
peak spur = -84.30 dB
LUT depth = 4096
LUT precision = 12b
PACC precision = 32b
f =
© Chris Dick 2004-2009DDS v2.1 12
Performance: Swept Tone
0 0.1 0.2 0.3 0.4 0.5
-120
-100
-80
-60
-40
-20
0
-72 dB
-84 dB
start sweep = 0.0313
end sweep = 0.0415
num sweeps = 10
∆ f = 0.00102
LUT Depth = 4096
LUT Precision = 16
PACC Precision = 32
04-Sep-2001 22:10:00
Frequency
dB
0 0.1 0.2 0.3 0.4 0.5
-120
-100
-80
-60
-40
-20
0
-72 dB
-84 dB
start sweep = 0.313
end sweep = 0.3415
num sweeps = 10
∆ f = 0.00285
LUT Depth = 4096
LUT Precision = 16
PACC Precision = 32
04-Sep-2001 22:16:06
Frequency
dB
0.00285
Start sweep = 0.313
end sweep = 0.3415
num sweeps = 10
LUT depth = 4096
LUT precision = 16b
PACC precision = 32b
f∆ =0.00102
Start sweep = 0.0313
end sweep = 0.0415
num sweeps = 10
LUT depth = 4096
LUT precision = 16b
PACC precision = 32b
f∆ =

7. Direct Digital Synthesis
7
© Chris Dick 2004-2009DDS v2.1 13
Implementation - Phase Trunc. DDS
• Phase truncation DDS: SFDR increases at a rate of 6 dB/bit of LUT
address
• For modest SFDR requirements phase truncation is an option, e.g.
SFDR=48 dB, 256 entry LUT
• Using 1/4-wave symmetry, 64 entry table is needed
• complex DDS employing distributed RAM will require 2 64 entry
tables - one for I one for Q
• 10b samples ⇒ 20 slices for I and 20 for Q
– this is ok
© Chris Dick 2004-2009DDS v2.1 14
Dithered DDS
• Phase dithering will purchase an additional 2 bits of
address space
0 0.1 0.2 0.3 0.4 0.5
-100
-80
-60
-40
-20
0
NORMALIZED FREQUENCY
DB
0 0.1 0.2 0.3 0.4 0.5
-100
-80
-60
-40
-20
0
NORMALIZED FREQUENCY
DB

8. Direct Digital Synthesis
8
© Chris Dick 2004-2009DDS v2.1 15
Implementation - Dithered DDS
• Dither signal generator requires only a modest amount of
silicon
• can choose to spend this optimization in several ways
– maintain table size and achieve higher spectral purity
– minimize hardware by using a LUT that is 1/4 the size of that
required by a phase truncation design
• This will still be a large amount of FPGA real-estate for
high performance applications
© Chris Dick 2004-2009DDS v2.1 16
Series-Corrected DDS
• Taylor series expansion
• Consider a two term expansion for sin(x) and cos(x)
2 ( )
( ) ( ) ( ) ( ) ( ) ( )
( ) ( )
1! 2! !
N N
x a f a x a f a x a f a
f x f a
N
′ ′′− − −
= + + +
sin( ) sin( ) ( )cos( )
cos( ) cos( ) ( )sin( )
x a x a a
x a x a a
= + −
= − −

9. Direct Digital Synthesis
9
© Chris Dick 2004-2009DDS v2.1 17
Taylor Series DDS
0 10 20 30 40 50 60 70 80 90 100
-1
-0.5
0
0.5
1
TIME
AMPLITUDE
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
-100
-80
-60
-40
-20
0
NORMALIZED FREQUENCY
DB
Phase
Increment
∆θ M
clk
Phase
Accumulator
(e.g. 32 bits)
Q( )
cos(θ(n))
sin(θ(n))
e.g. N = 8
+ -
N
Sine
Cosine
Lookup
Table
-
θ(n) θ(n)^
cos θ(n)^
sin θ(n)^
{+cos(θ(n)), -sin (θ(n))}
© Chris Dick 2004-2009DDS v2.1 18
Implementation - Taylor Series DDS
Several arithmetic units required ⇒consider for applications
that require very high spur suppression
Virtex-II embedded multipliers well suited to this architecture
Phase
Increment
∆θ M
clk
Phase
Accumulator
(e.g. 32 bits)
Q( )
cos(θ(n))
sin(θ(n))
e.g. N = 8
+ -
N
Sine
Cosine
Lookup
Table
-
θ(n) θ(n)^
cos θ(n)^
sin θ(n)^

10. Direct Digital Synthesis
10
© Chris Dick 2004-2009DDS v2.1 19
Implementation - Taylor Series DDS
• 1 block RAM
• 2 MPY
• 1 MPY by a constant
0 0.5
-100
-50
0
(a)
DB
0 0.5
-100
-50
0
(b)
DB
0 0.5
-100
-50
0
(c)
DB
0 0.5
-100
-50
0
(d)
DB
-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5
-140
-120
-100
-80
-60
-40
-20
0
Frequency
dB
LUT Depth = 4096
LUT Precision = 18
Output Precision = 20
f0 = 0.002433
09-Jul-2003 19:09:19
© Chris Dick 2004-2009DDS v2.1 20
System Generator DDS
• Taylor Series DDS
Pipeline balancing registers
Taylor series correction mpy
Compute error signal
Phase
acc.
Quantize phase acc.

11. Direct Digital Synthesis
11
© Chris Dick 2004-2009DDS v2.1 21
Performance
-0.5 0 0.5
-140
-120
-100
-80
-60
-40
-20
0
Frequency
DB
LUT Depth = 4096
LUT Precision = 18
Output Precision = 20
f0 = 0.0893
02-Jun-2002 23:38:52
-115 dB
© Chris Dick 2004-2009DDS v2.1 22
Design Statistics
• Tools
– System Generator v3.1
– ISE 5.2.03i speedfile: ADVANCED 1.78 2003-05-0
• Device = XC2VP501152-7
• 216 logic slices (3-level pipelined mpys)
• 1 block RAM
• 2 18x18 embedded multipliers
• fclk max = 179 MHz

12. Direct Digital Synthesis
12
© Chris Dick 2004-2009DDS v2.1 23
Multi-Channel DDS
• Build M-channel DDS (M-ary DDS)
• Multi-channel DDS can be constructed for almost
the same cost as a single DDS
• Time division multiplex the hardware
• Each DDS operates at 1/M’th the clock rate
• For fclk = 120 MHz and M=3, each DDS will
operate at a rate of 40 MHz
© Chris Dick 2004-2009DDS v2.1 24
Virtex Slice Revision
D Q
CE
D Q
CE
D Q
CE
D Q
CE
LUT
IN
CE
CLK
ADDRESS
OUT
CASCADE

13. Direct Digital Synthesis
13
© Chris Dick 2004-2009DDS v2.1 25
Multi-Channel DDS
• Make use of SRL16s to efficiently implement the
M phase accumulators (PACCs)
z-1
Phase
Increment
Memory
0,1, , 1i i Mθ = −…
Address
Generator
ROM or Dual-port RAM
Microblaze
Power PC
or MPU external to FPGA
supplies phase
increment values
SRL16-based
registers
PACC FILE
© Chris Dick 2004-2009DDS v2.1 26
Multi-Channel DDS
• PACC file is efficiently implemented using the
SRL16 slice configuration
z-1
Phase
Increment
Memory
0,1, , 1i i Mθ = −…
Address
Generator
ROM or Dual-port RAM
SRL16-based
registers
PACC FILE
B
16 B-bit precision PACCs can be supported
using B/2 slices
16 32b PACCs requires 16 slices + 16 slices
for the adder and delay

14. Direct Digital Synthesis
14
© Chris Dick 2004-2009DDS v2.1 27
Multi-Channel DDS
• Small cost to de-multiplex the outputs
• The cost to demux each Bo-bit output is ~ Bo/2 slices
z0 M 0 ( )y n
z-1 M 1( )y n
z-M+1 M 1( )My n−
DDS
De-multiplexed
output time-series
Bo
© Chris Dick 2004-2009DDS v2.1 28
M-ary Phase Accumulator
Phase increment memory
SRL16-based phase accumulators
Sum & Delay
• In this case the phase increment values are stored in
ROM since they are known prior to run-time
• Alternatively dual-port memory could be used of the
output frequencies need to be updated at run-time

15. Direct Digital Synthesis
15
© Chris Dick 2004-2009DDS v2.1 29
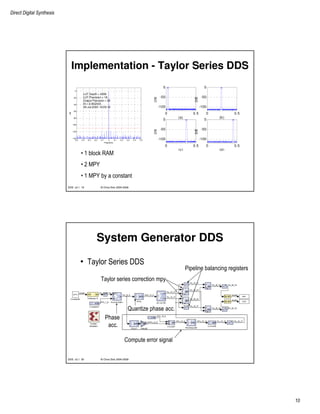
M-ary Taylor Series DDS
Channel demultiplexing
M-ary phase accumulator
DDS
© Chris Dick 2004-2009DDS v2.1 30
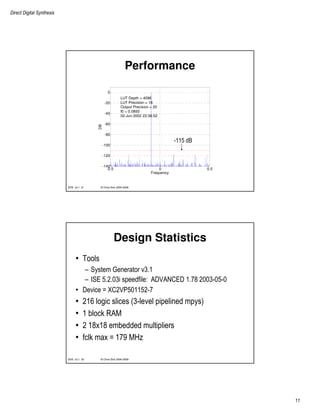
3-Channel Taylor Series DDS
-0.5 0 0.5
-140
-120
-100
-80
-60
-40
-20
0
Frequency
DB
LUT Depth = 4096
LUT Precision = 18
Output Precision = 20
f = [0.1, 0.2, 0.3]
09-Jun-2002 11:37:14
• 3 tones efficiently generated
by time sharing the hardware
• Sample-rate versus area
tradeoff

16. Direct Digital Synthesis
16
© Chris Dick 2004-2009DDS v2.1 31
M-ary Phase Truncation DDS
Phase increment memory
SRL16-based phase accumulators
Sum & Delay
Trig LUT
Output
Demux
© Chris Dick 2004-2009DDS v2.1 32
8-Channel Phase Truncation DDS
-0.5 0 0.5
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
Frequency
DB
LUT Depth = 4096
LUT Precision = 16
09-Jun-2002 13:02:48
• 1 demultiplexed output
• Very compact design

17. Direct Digital Synthesis
17
© Chris Dick 2004-2009DDS v2.1 33
CORDIC DDS
-0.5 0 0.5
-100
-50
0
F
dB
Precision = 12 bits
Num Iterations = 12
f = 0.01
09-Jun-2002 14:34:39
-0.5 0 0.5
-100
-50
0
F
dB
Precision = 12 bits
Num Iterations = 14
f = 0.01
09-Jun-2002 14:34:41
-0.5 0 0.5
-100
-50
0
F
dB
Precision = 12 bits
Num Iterations = 16
f = 0.01
09-Jun-2002 14:34:43
-0.5 0 0.5
-100
-50
0
F
dB
Precision = 12 bits
Num Iterations = 18
f = 0.01
09-Jun-2002 14:34:45
© Chris Dick 2004-2009DDS v2.1 34
CORDIC DDS
-0.5 0 0.5
-100
-50
0
F
dB
Precision = 16 bits
Num Iterations = 12
f = 0.01
09-Jun-2002 14:38:34
-0.5 0 0.5
-100
-50
0
F
dB
Precision = 16 bits
Num Iterations = 16
f = 0.01
09-Jun-2002 14:38:36
-0.5 0 0.5
-100
-50
0
F
dB
Precision = 16 bits
Num Iterations = 18
f = 0.01
09-Jun-2002 14:38:39
-0.5 0 0.5
-100
-50
0
F
dB
Precision = 16 bits
Num Iterations = 20
f = 0.01
09-Jun-2002 14:38:41

18. Direct Digital Synthesis
18
© Chris Dick 2004-2009DDS v2.1 35
CORDIC DDS
-0.5 0 0.5
-100
-50
0
F
dB
Precision = 20 bits
Num Iterations = 8
f = 0.01
09-Jun-2002 14:41:03
-0.5 0 0.5
-100
-50
0
F
dB
Precision = 20 bits
Num Iterations = 12
f = 0.01
09-Jun-2002 14:41:05
-0.5 0 0.5
-100
-50
0
F
dB
Precision = 20 bits
Num Iterations = 16
f = 0.01
09-Jun-2002 14:41:07
-0.5 0 0.5
-100
-50
0
F
dB
Precision = 20 bits
Num Iterations = 18
f = 0.01
09-Jun-2002 14:41:09