Downloaded 97 times
Uploaded byMedia4math
Tutorials--Distance Formula
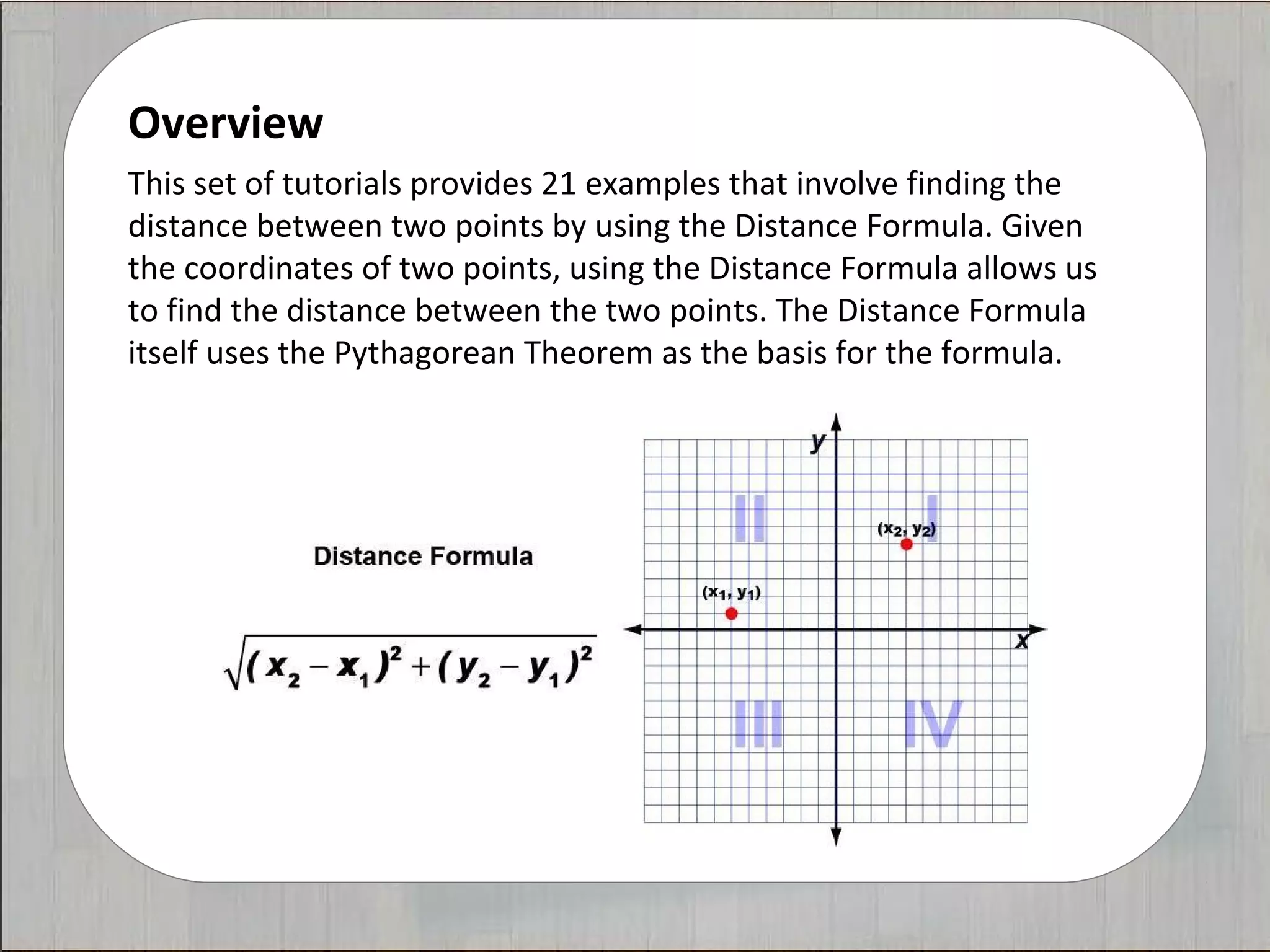
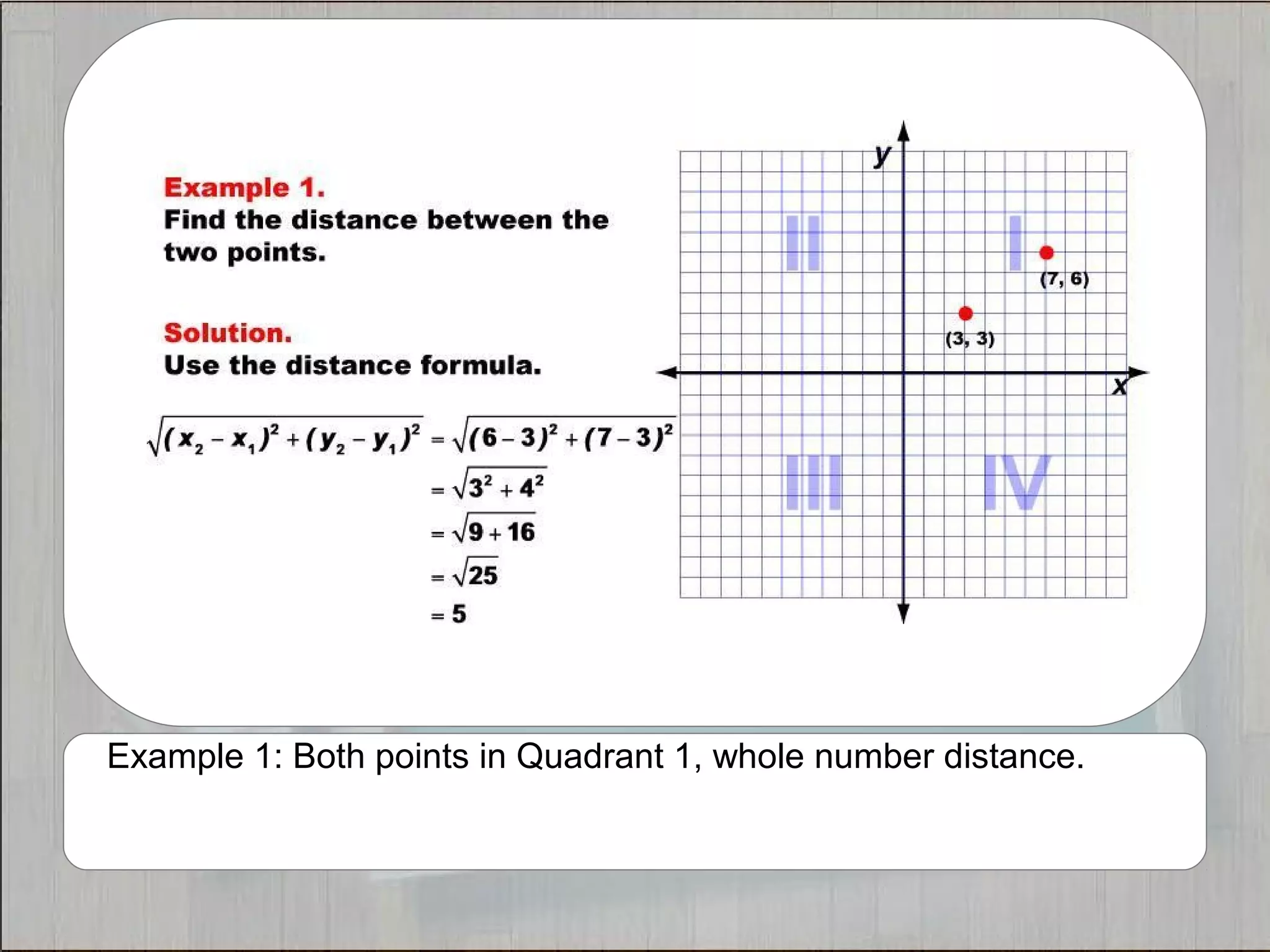
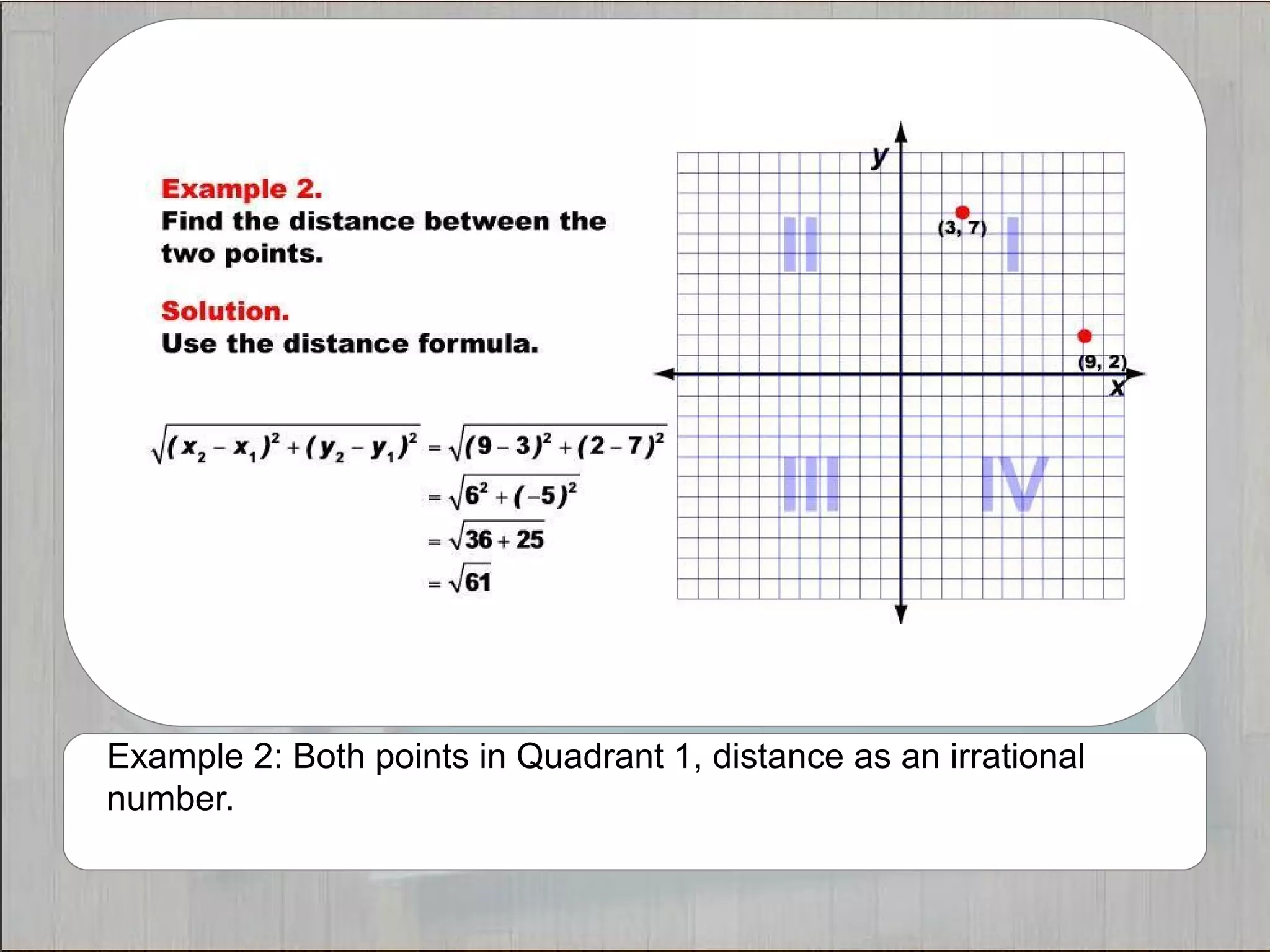
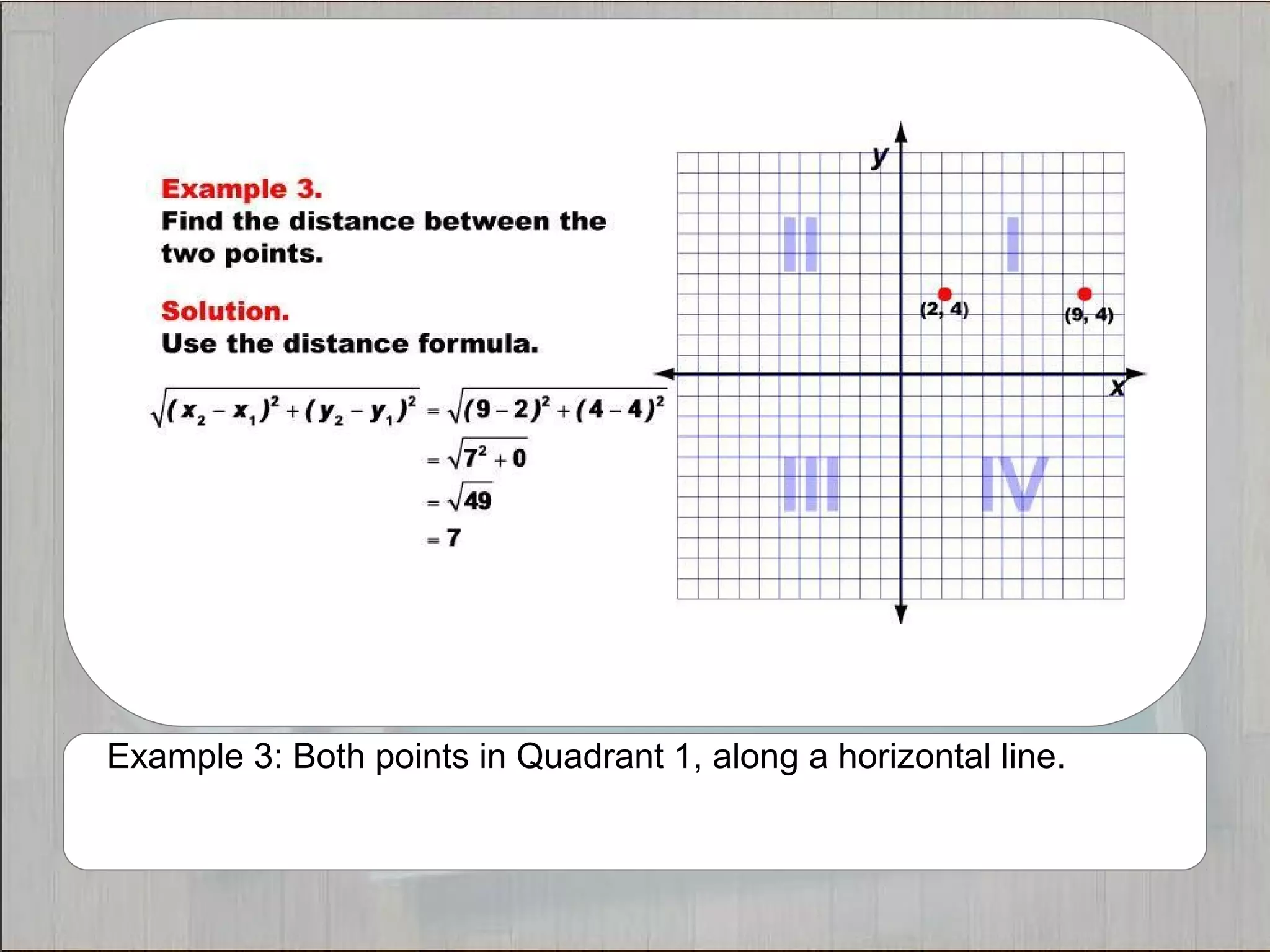
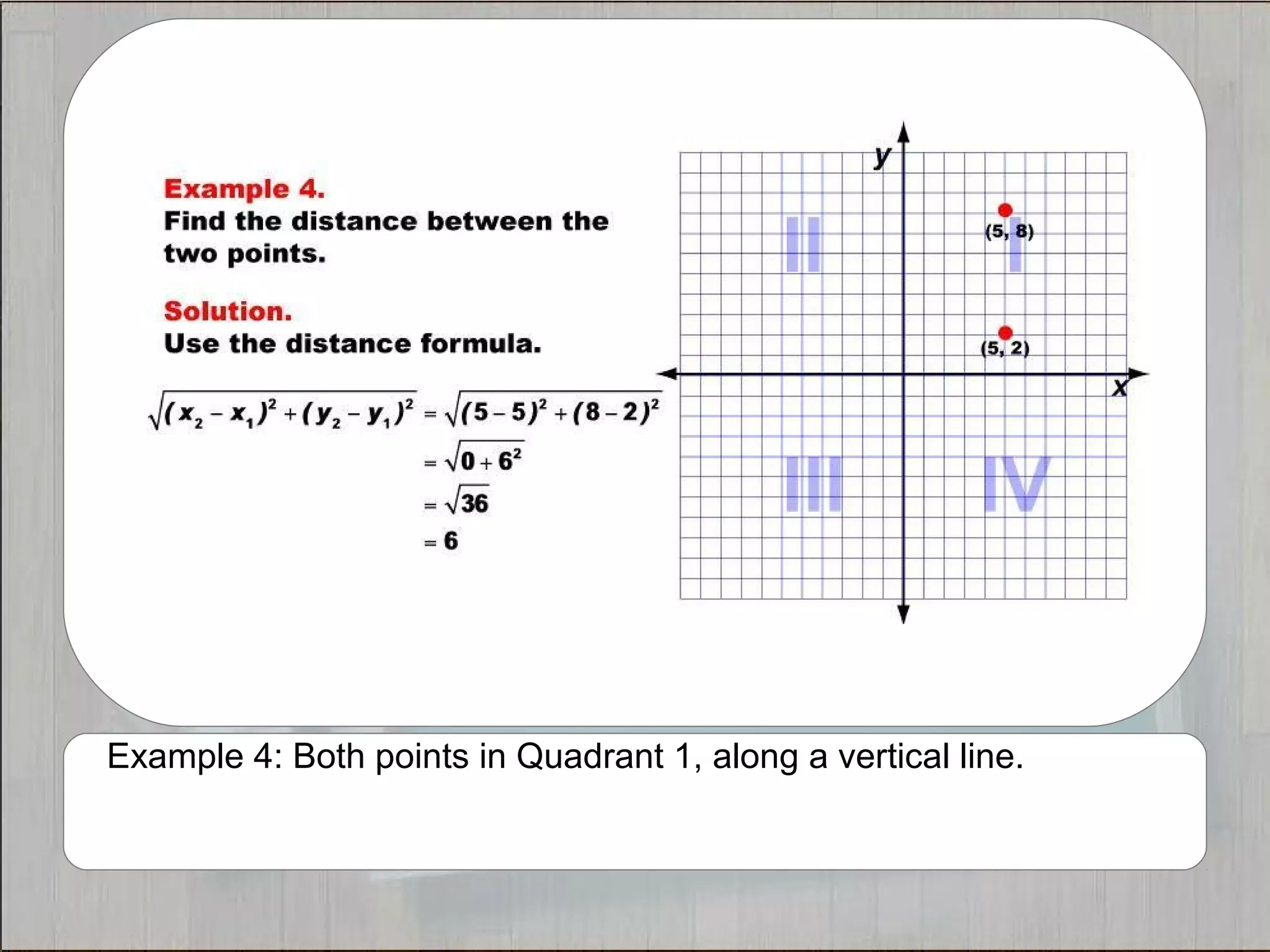
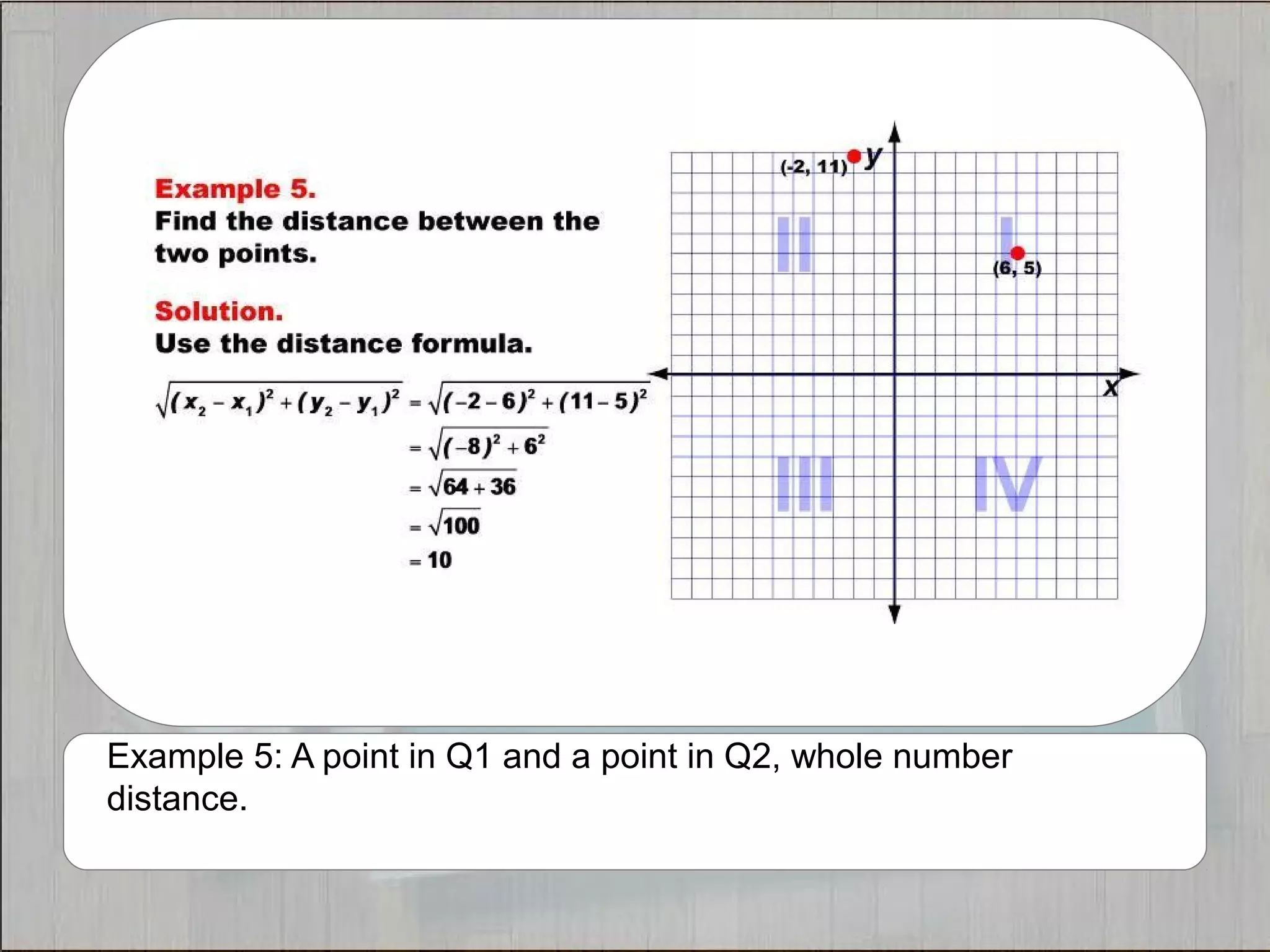
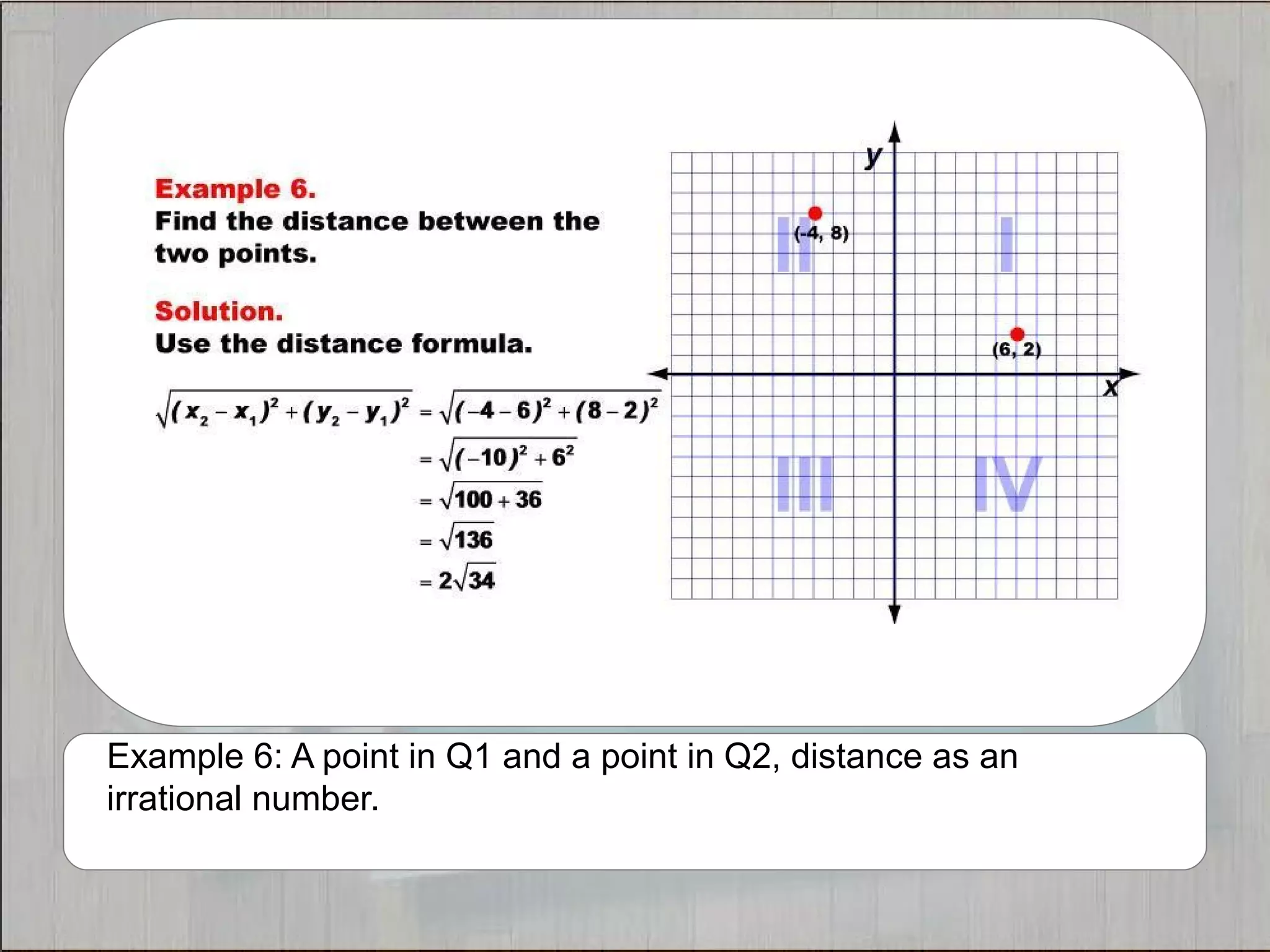
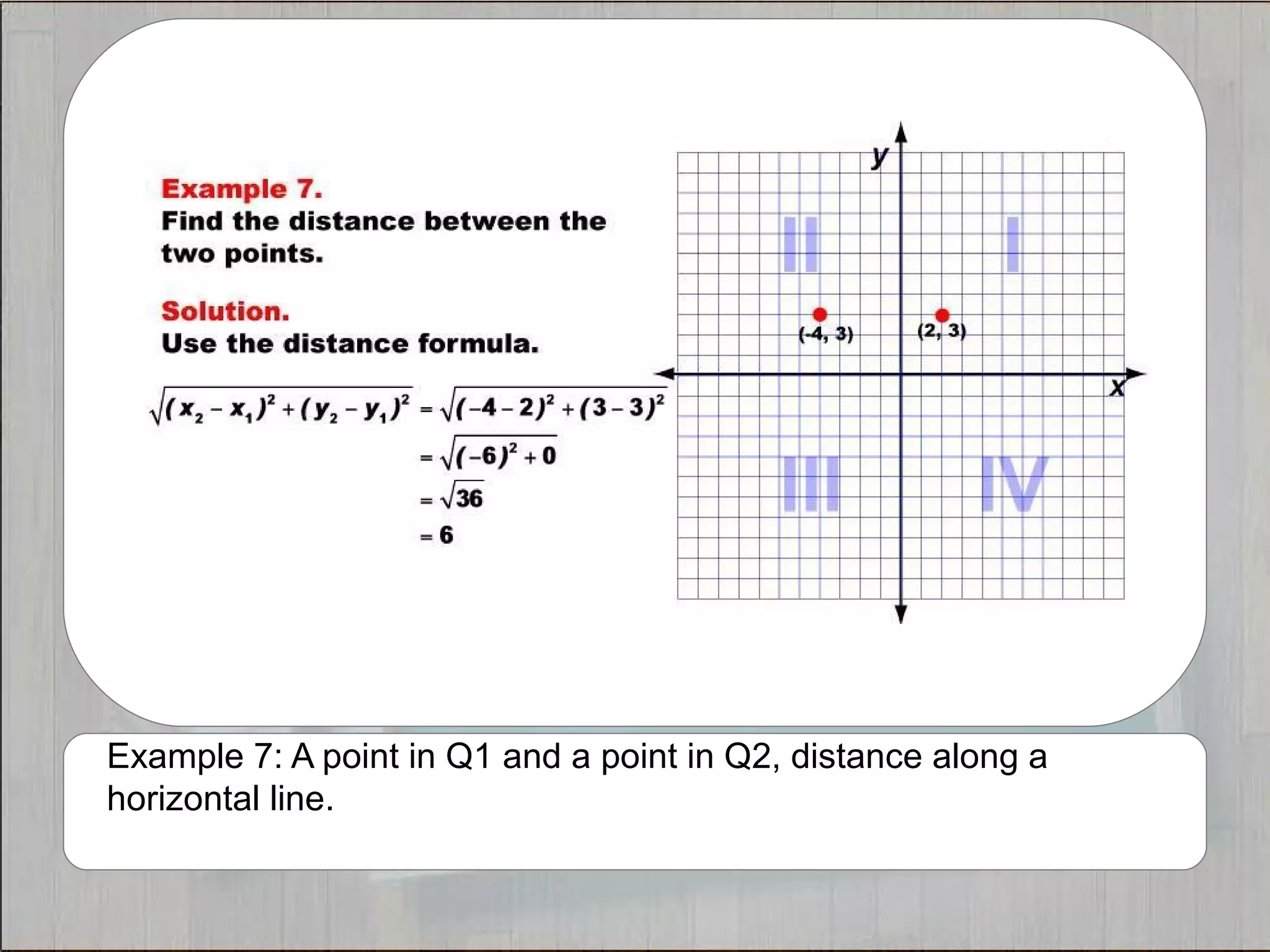
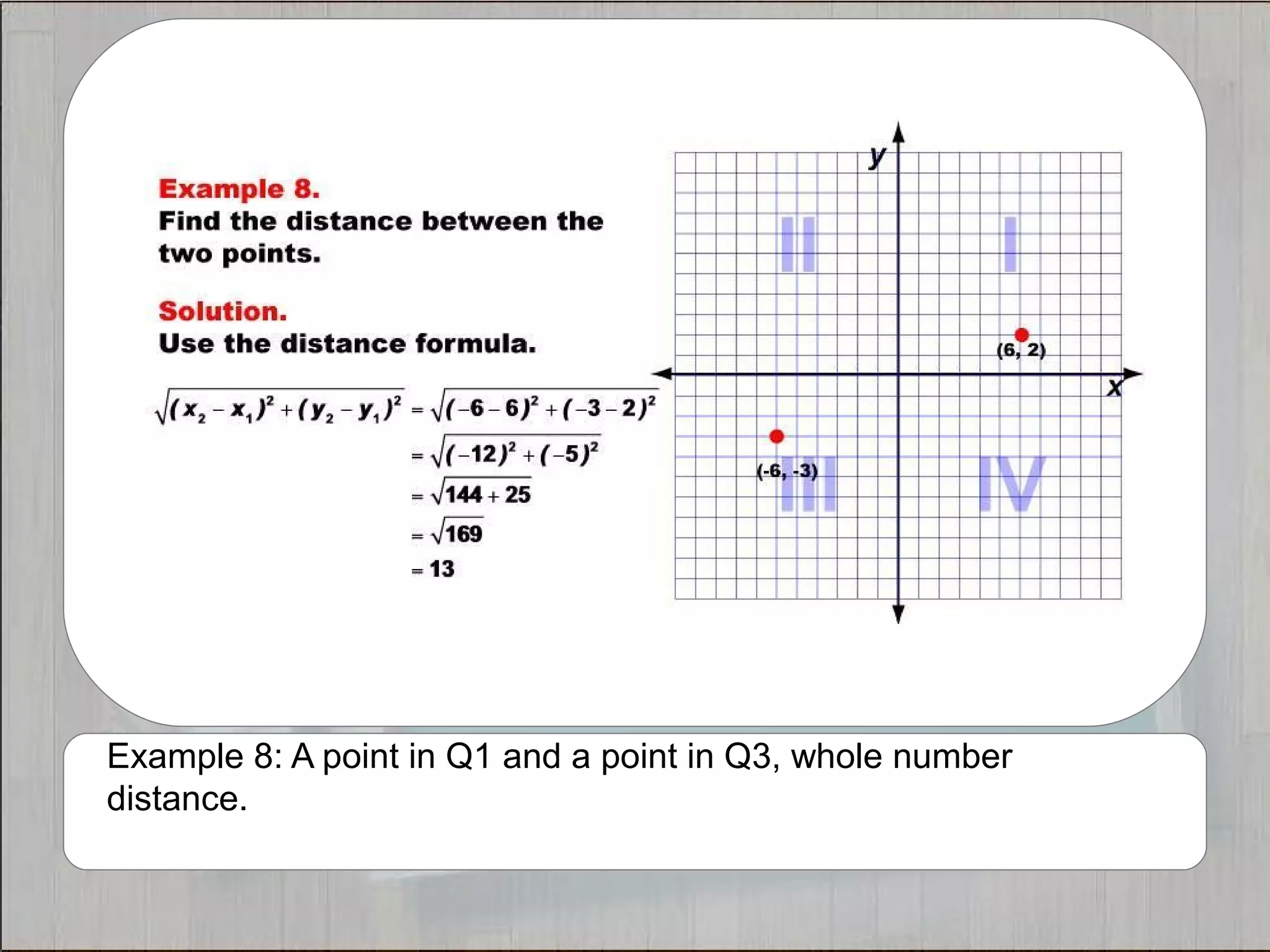
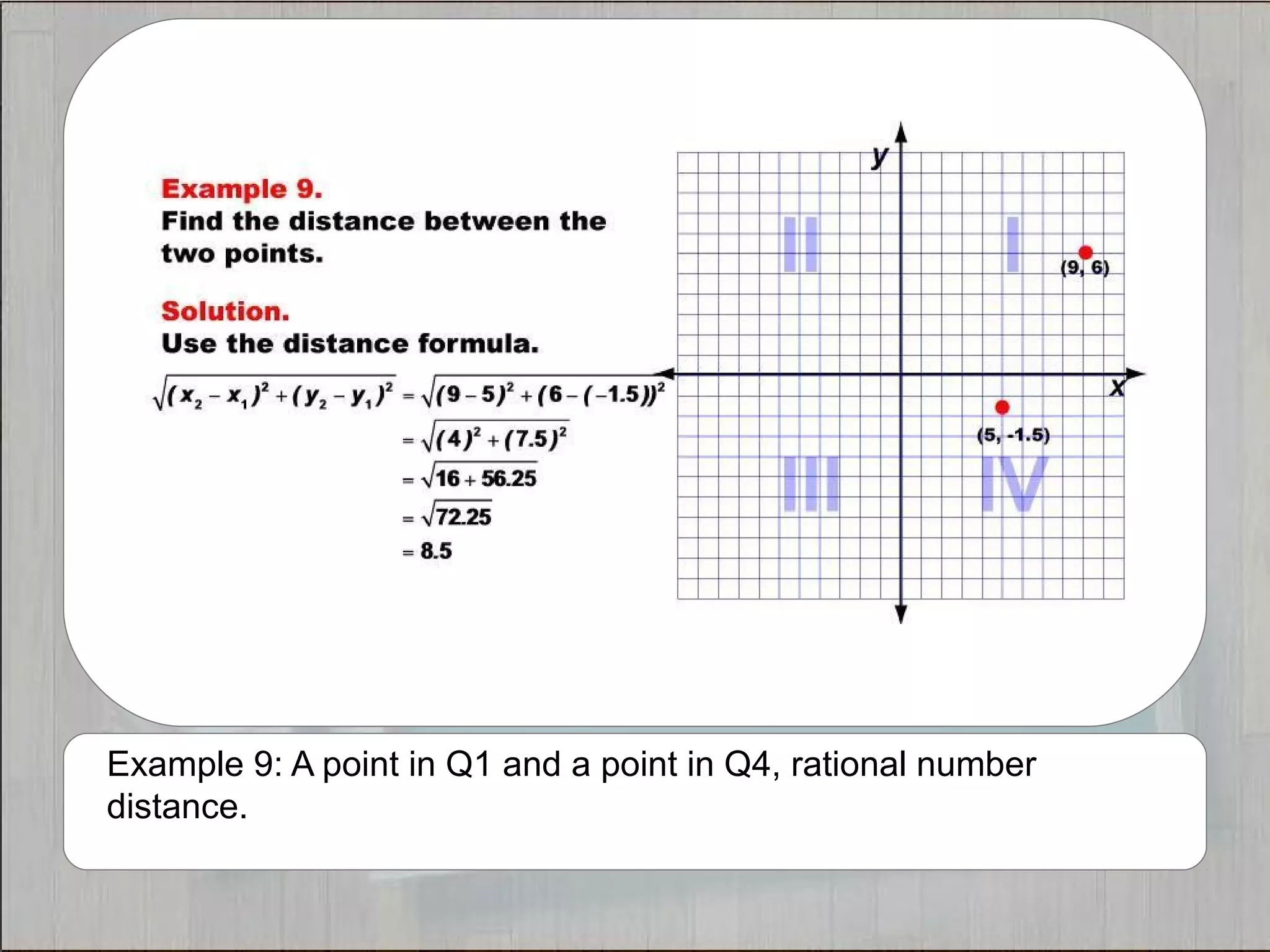
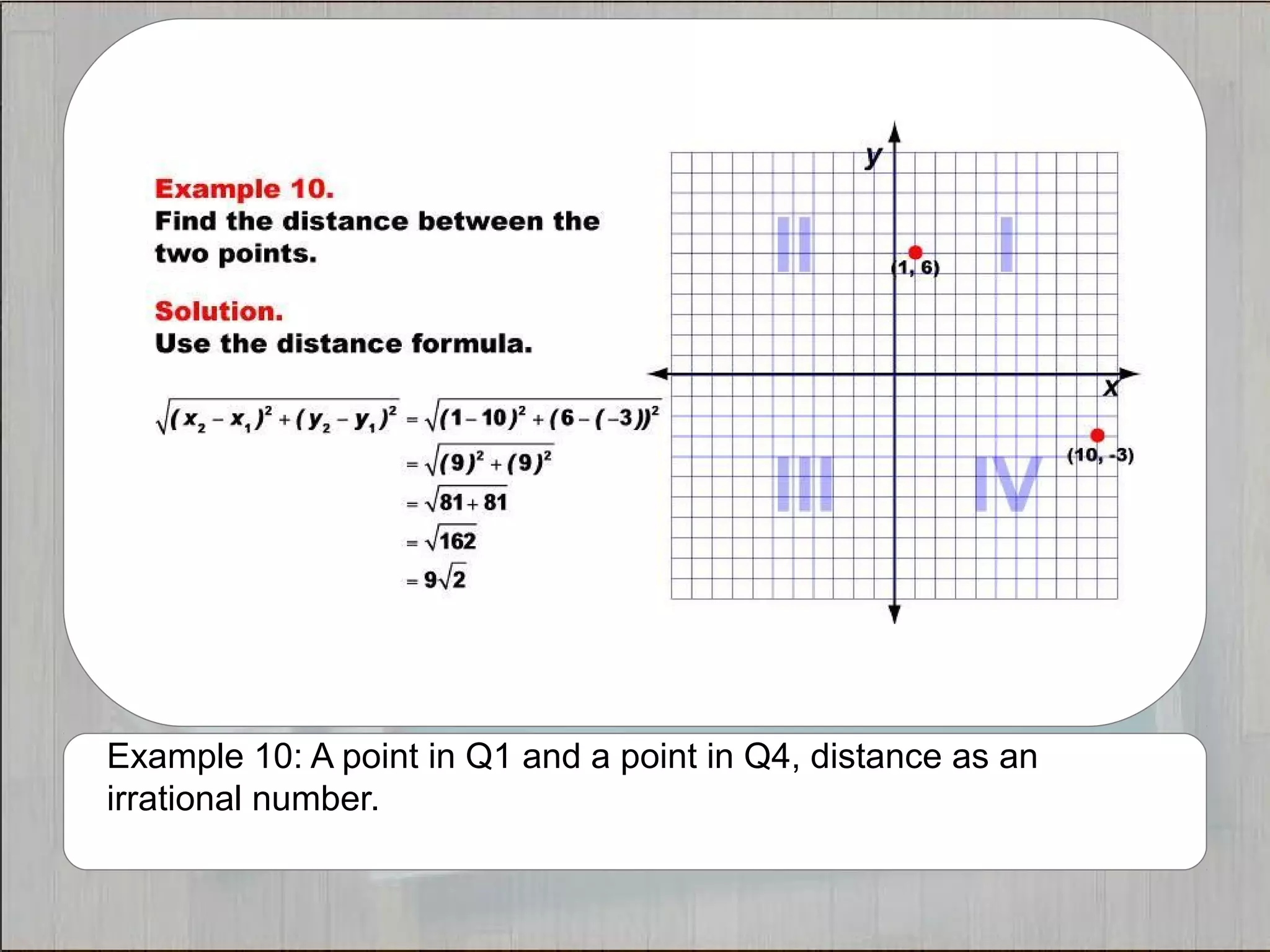
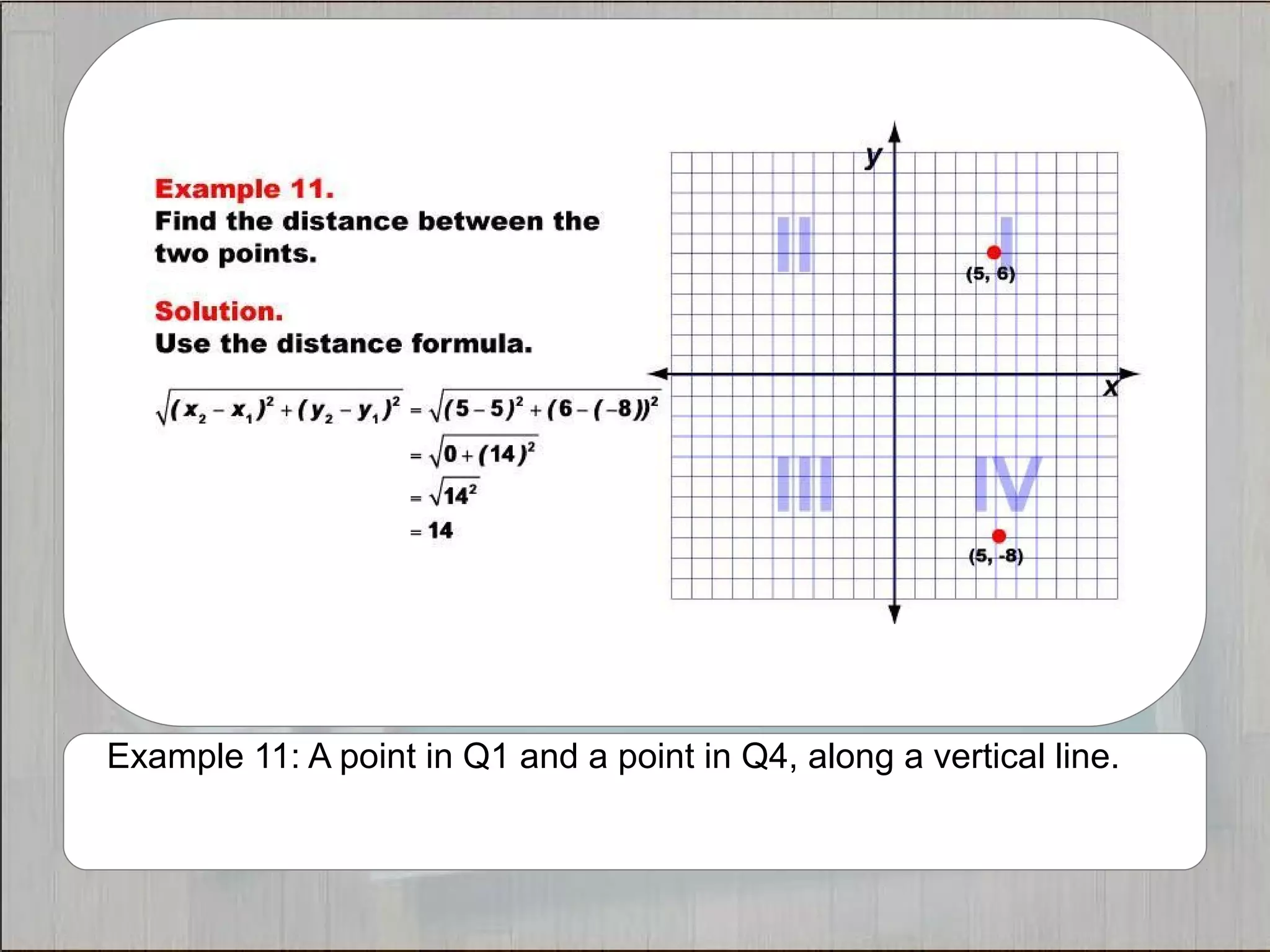
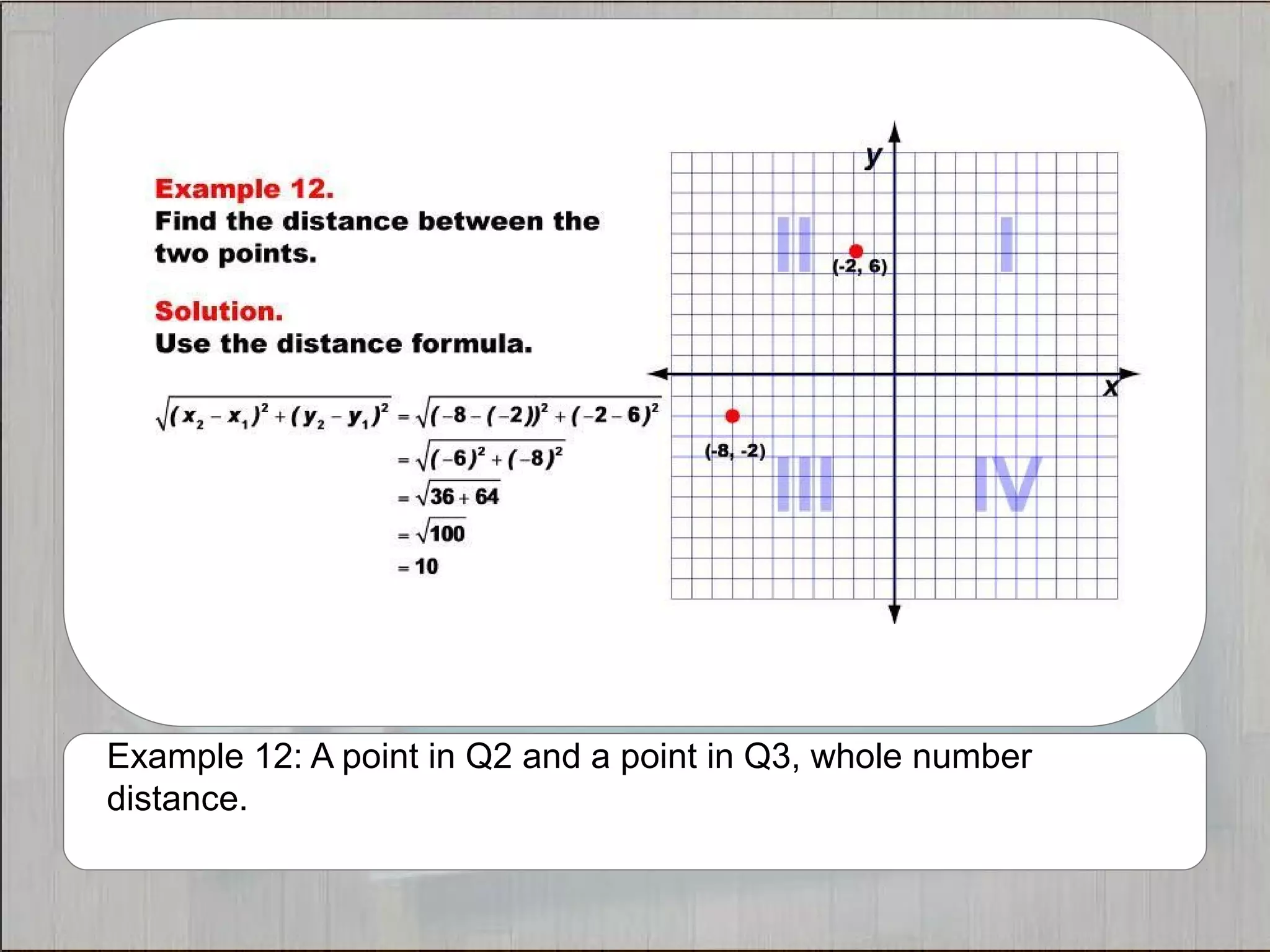
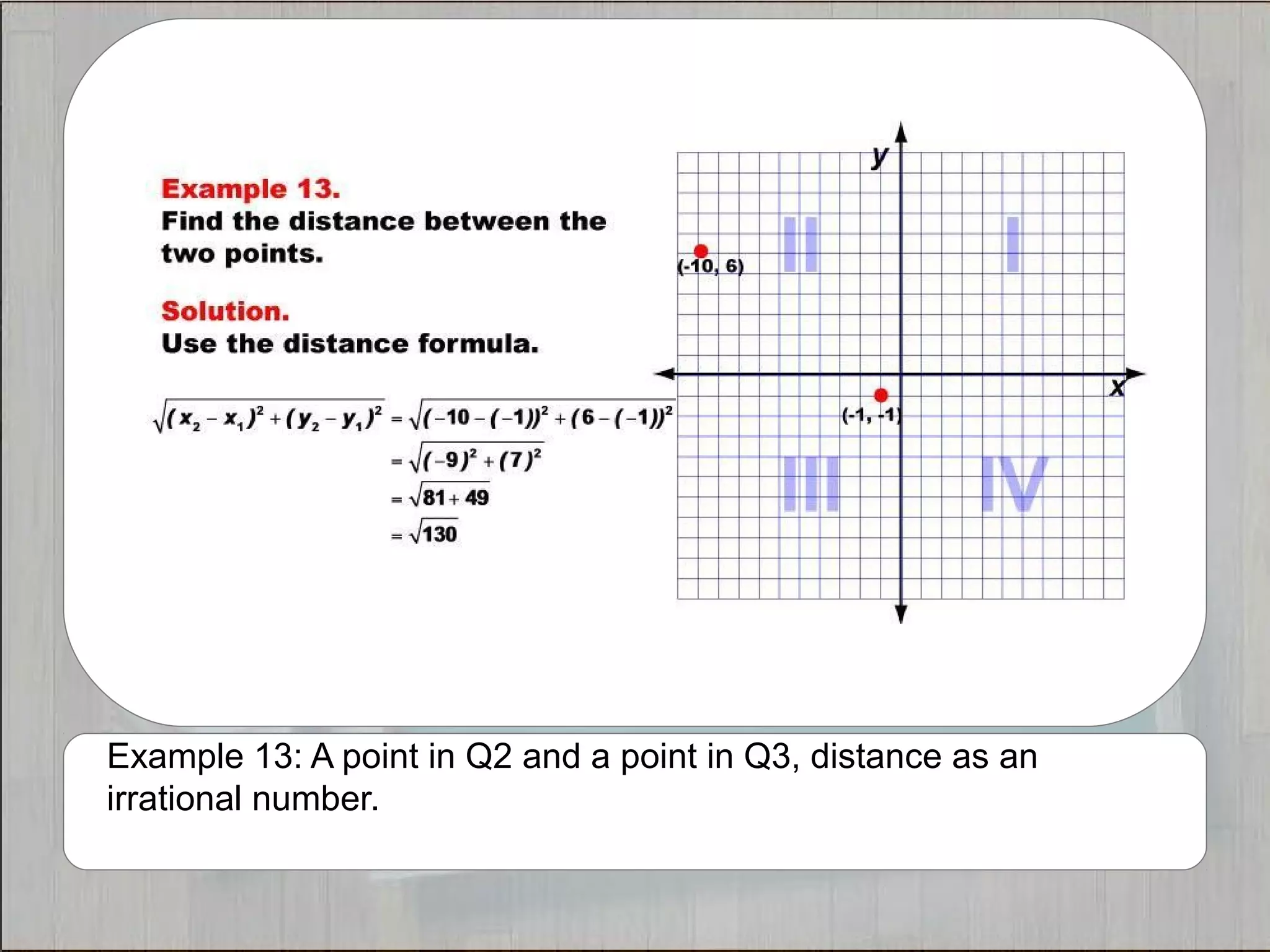
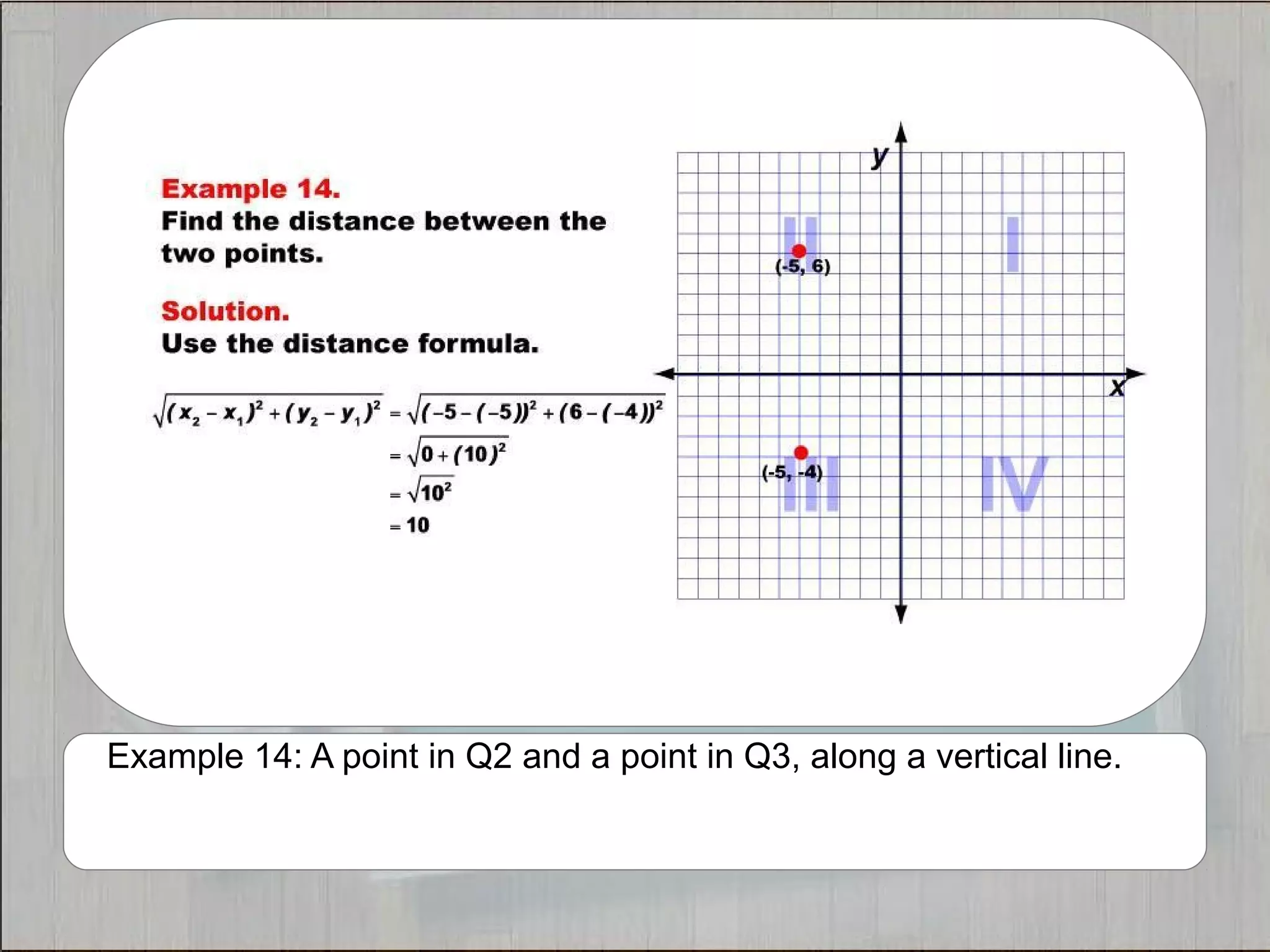
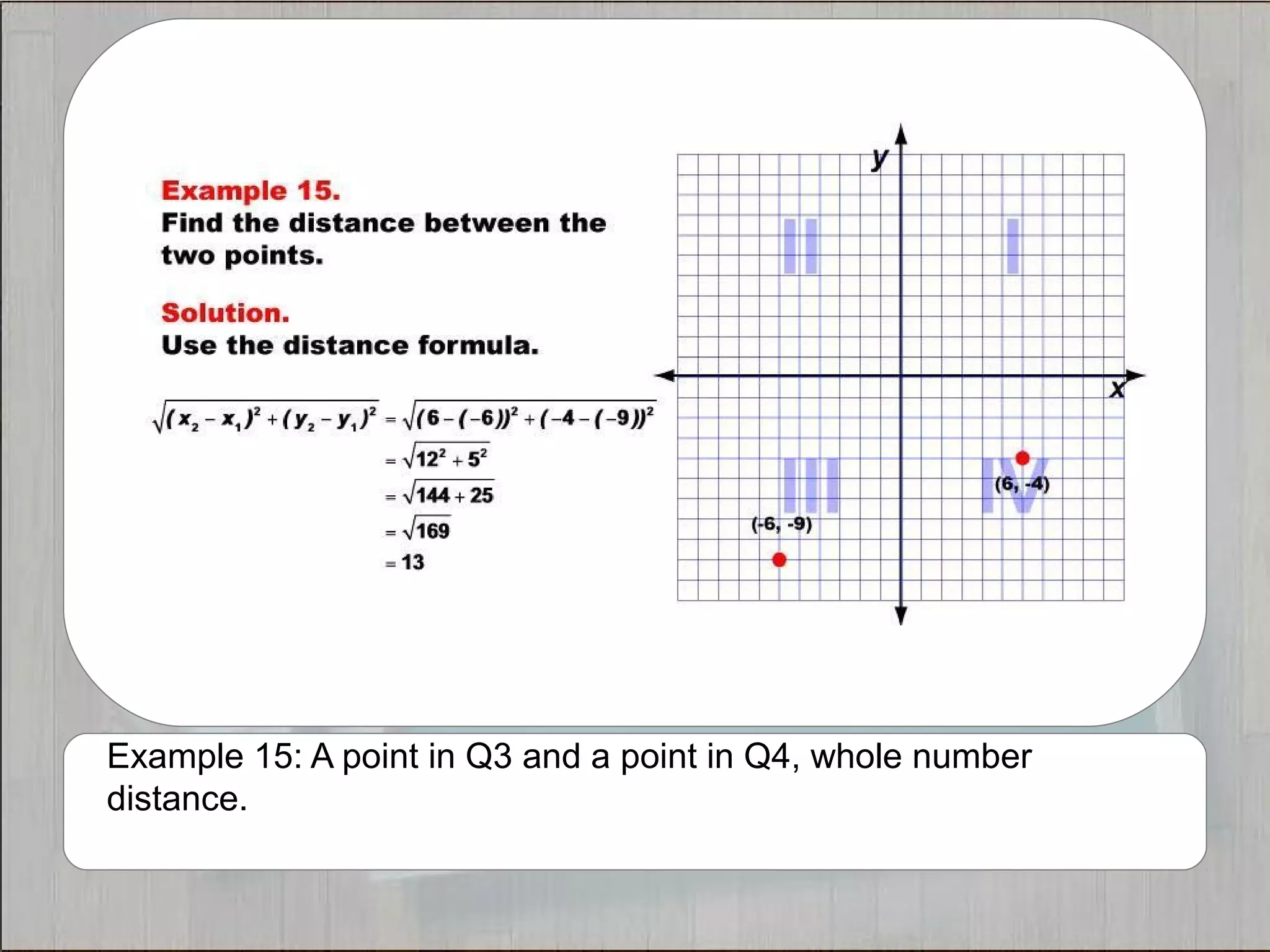
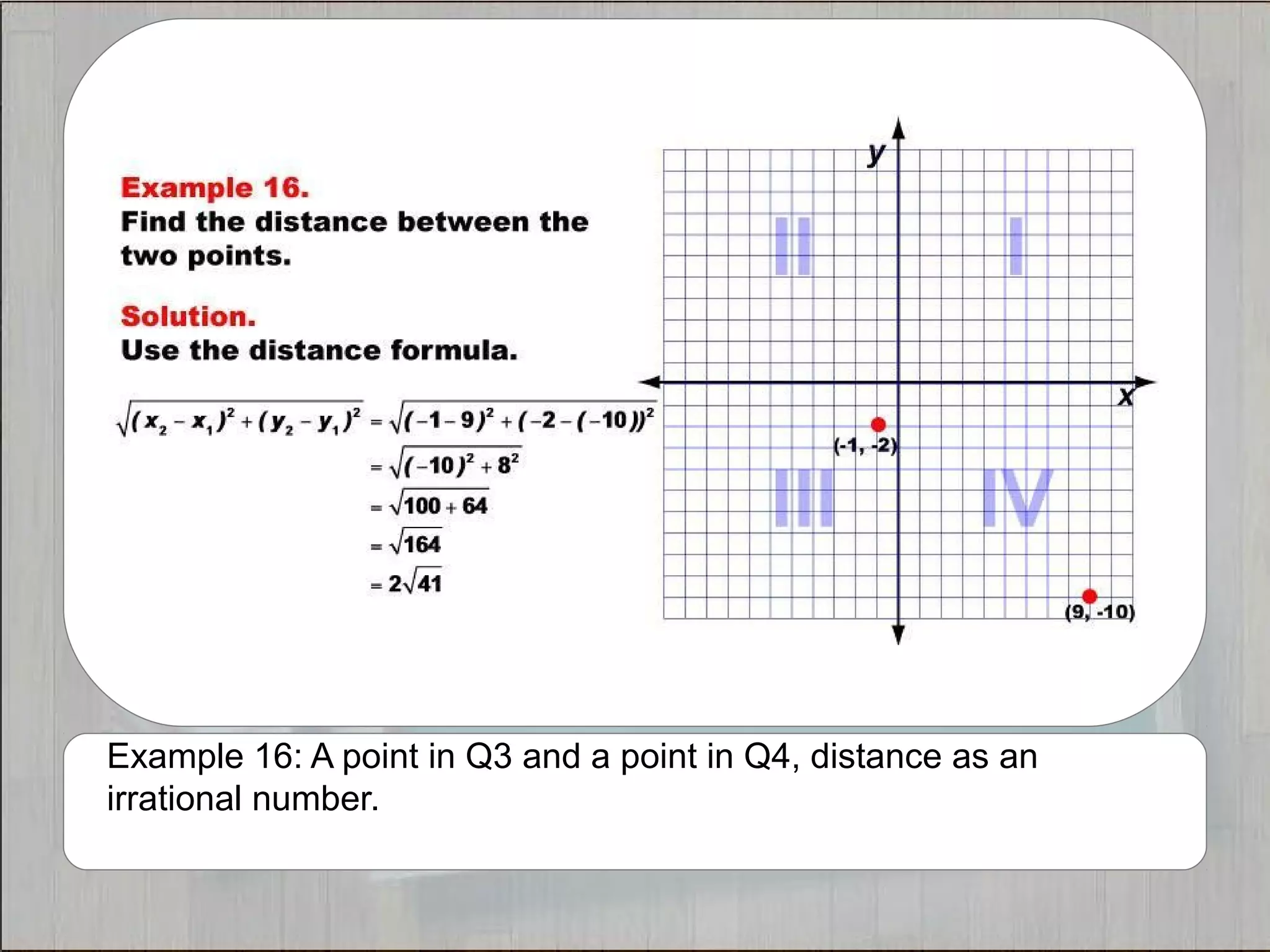
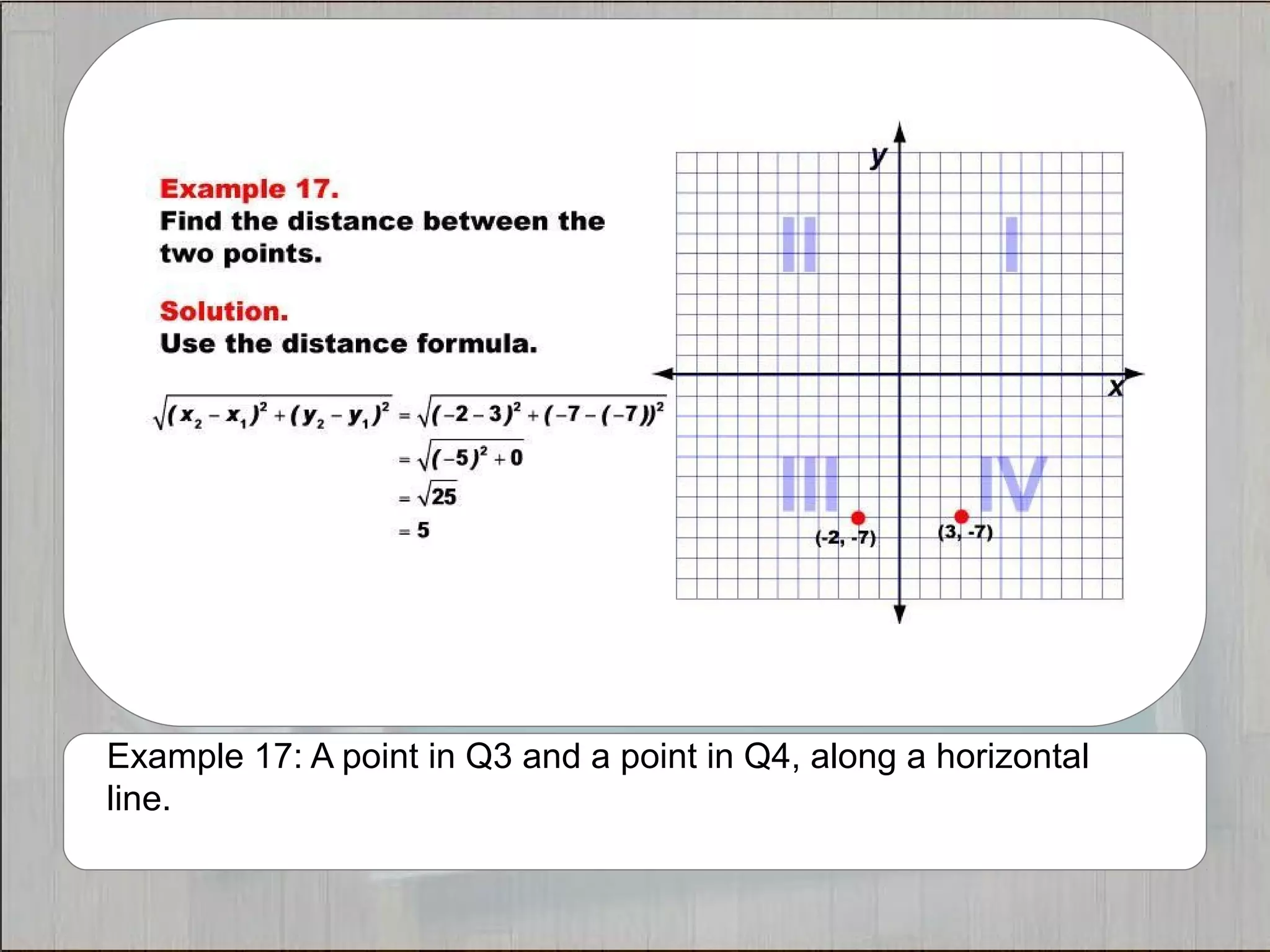
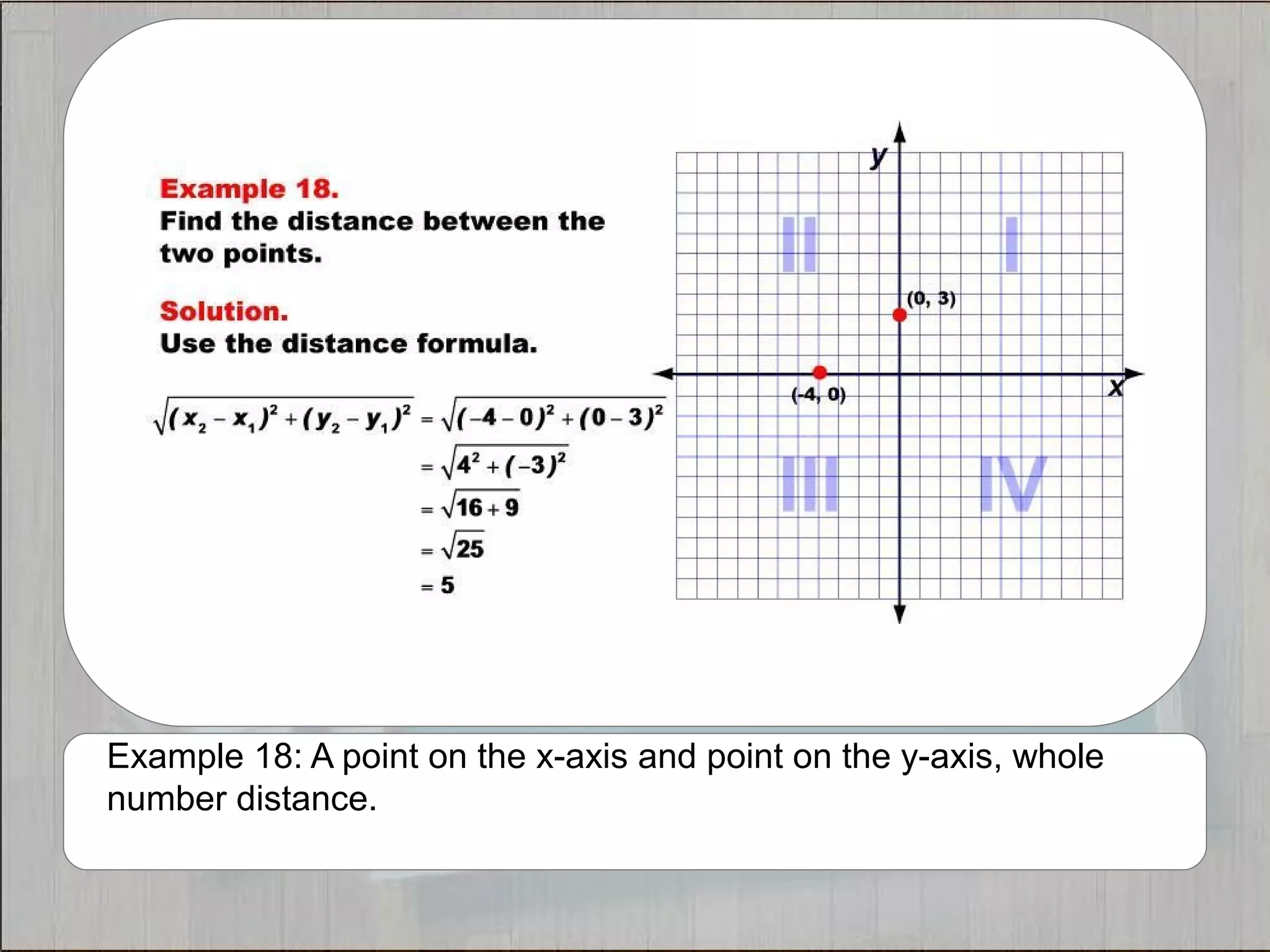
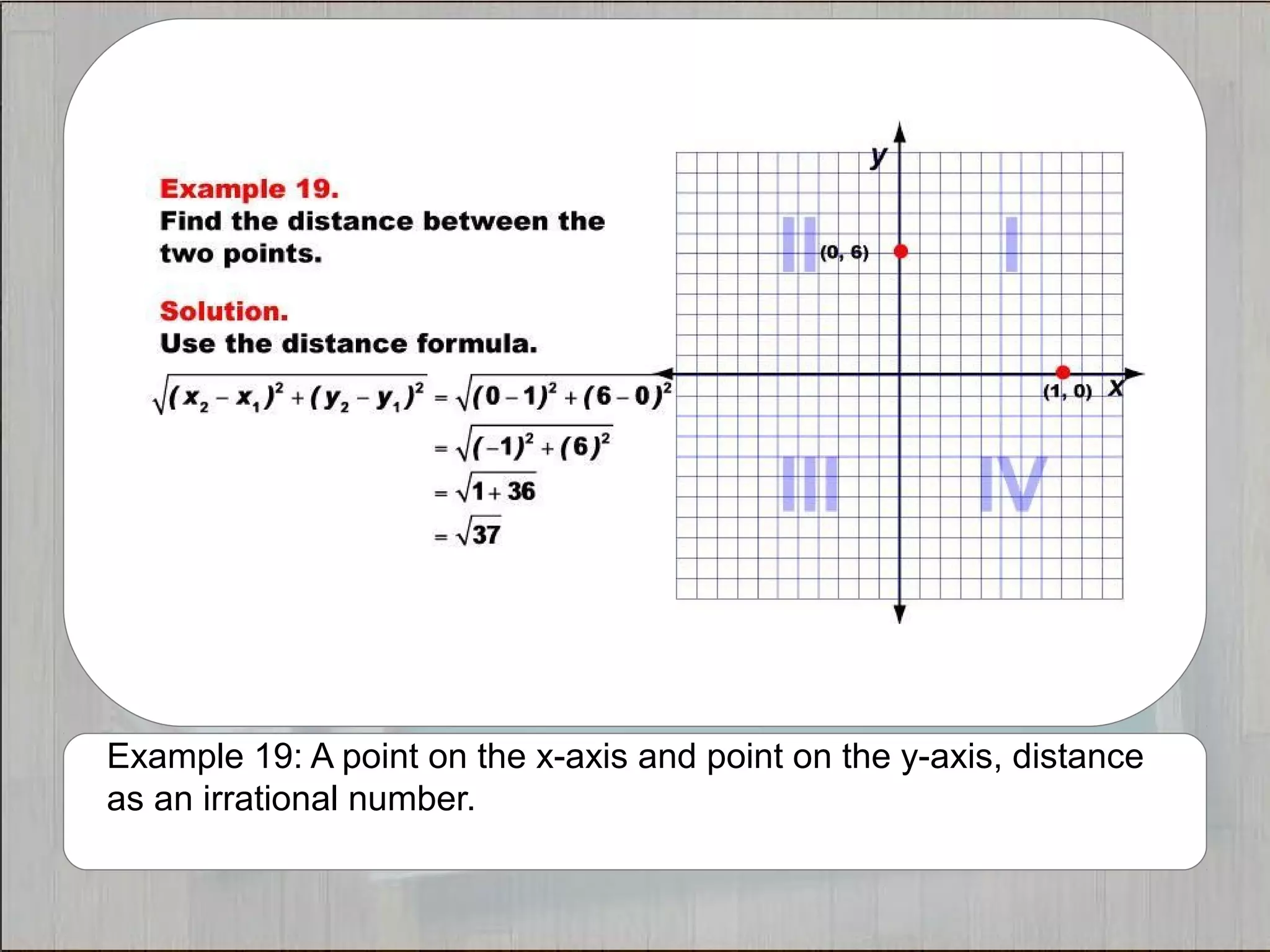
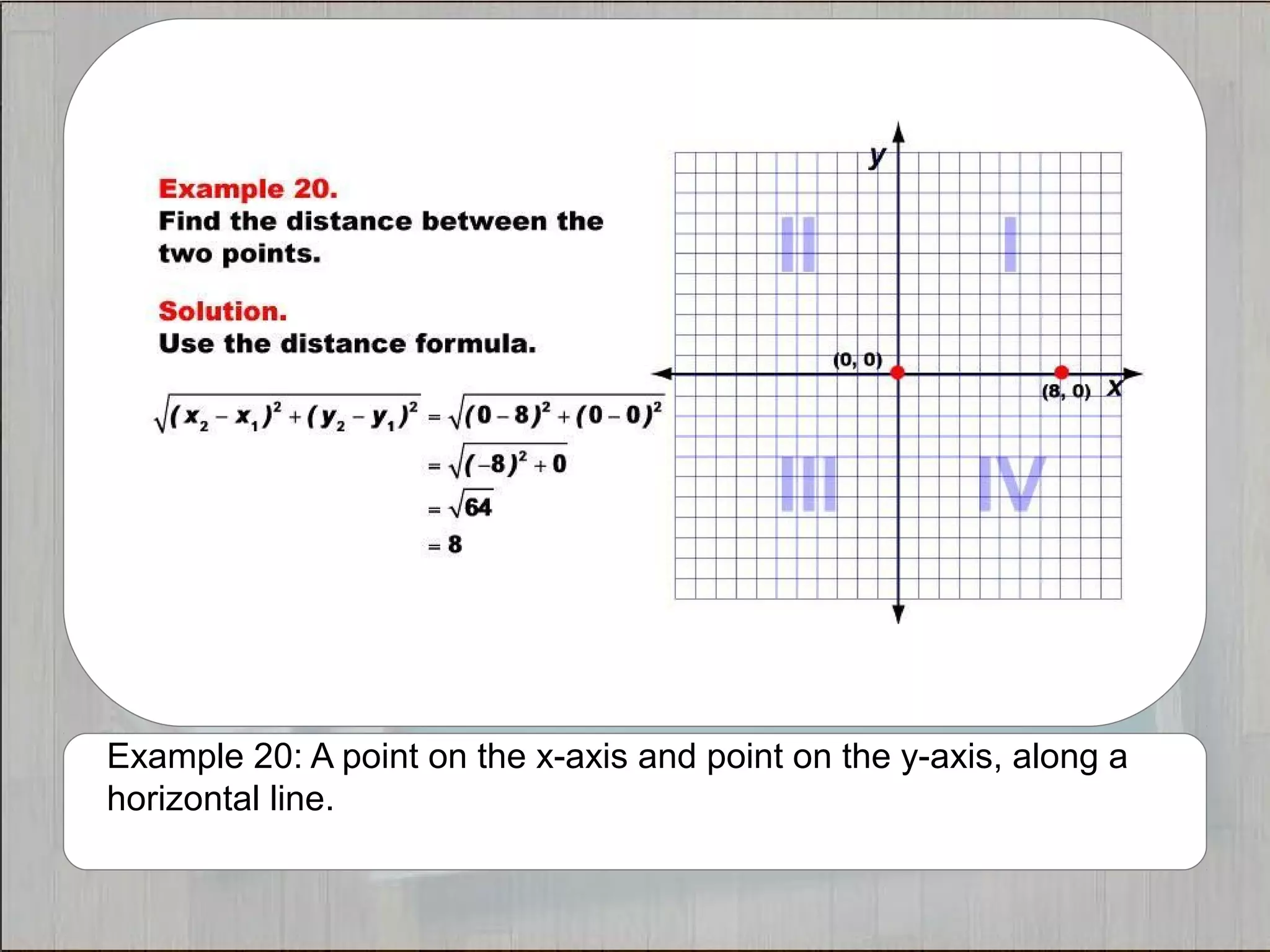
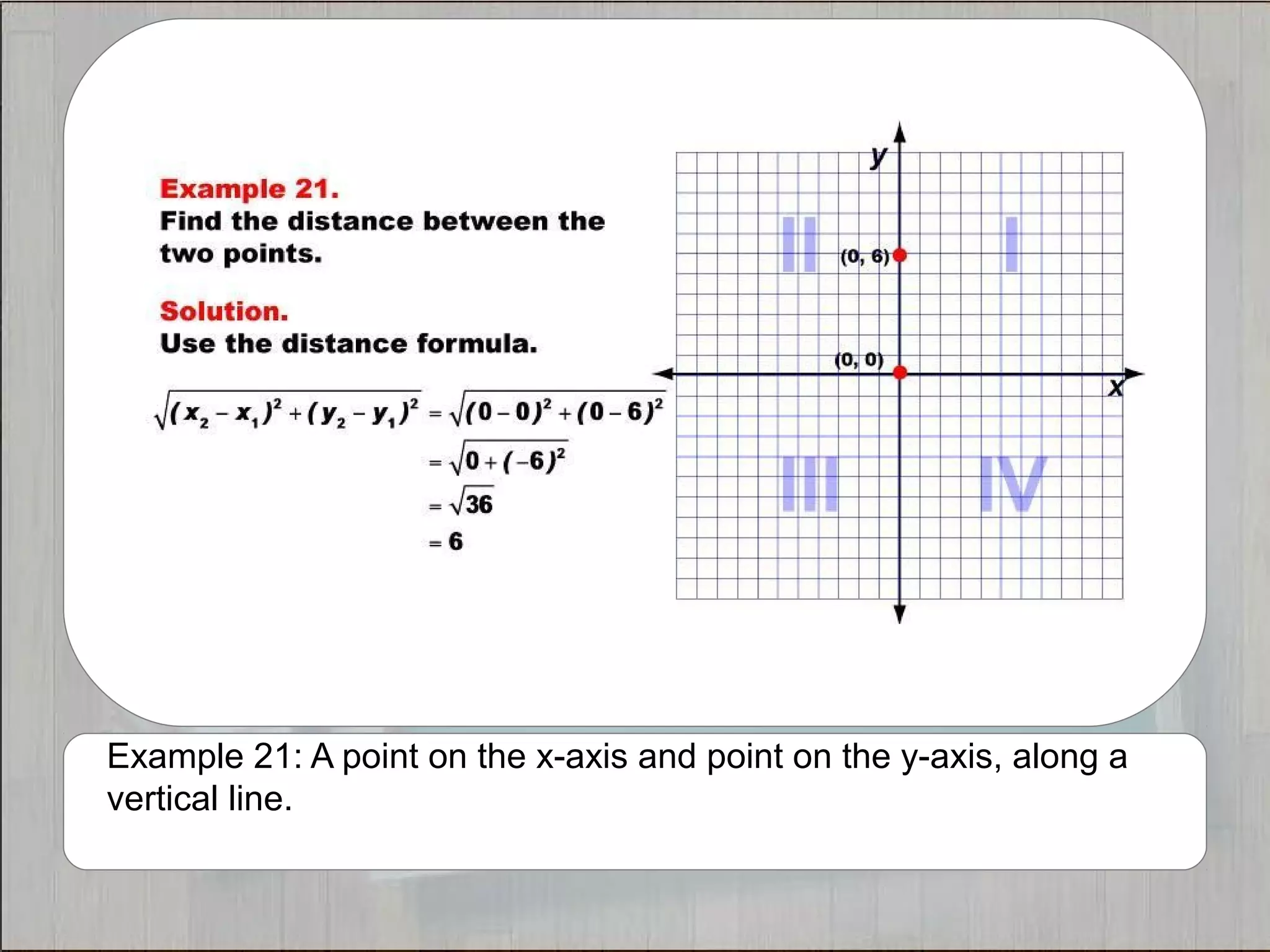
This document provides 21 examples of using the Distance Formula to calculate the distance between two points with different coordinates. The Distance Formula uses the Pythagorean Theorem as the basis for finding the distance between any two points given their x- and y-coordinates. Each example solves for the distance between points located in different quadrants or along the x- or y-axis.
More Related Content
Similar to Tutorials--Distance Formula
Tutorials--Distance Formula
- 1.
- 2. Overview This setof tutorials provides 21 examples that involve finding the distance between two points by using the Distance Formula. Given the coordinates of two points, using the Distance Formula allows us to find the distance between the two points. The Distance Formula itself uses the Pythagorean Theorem as the basis for the formula.
- 3. Example 1: Bothpoints in Quadrant 1, whole number distance.
- 4. Example 2: Bothpoints in Quadrant 1, distance as an irrational number.
- 5. Example 3: Bothpoints in Quadrant 1, along a horizontal line.
- 6. Example 4: Bothpoints in Quadrant 1, along a vertical line.
- 7. Example 5: Apoint in Q1 and a point in Q2, whole number distance.
- 8. Example 6: Apoint in Q1 and a point in Q2, distance as an irrational number.
- 9. Example 7: Apoint in Q1 and a point in Q2, distance along a horizontal line.
- 10. Example 8: Apoint in Q1 and a point in Q3, whole number distance.
- 11. Example 9: Apoint in Q1 and a point in Q4, rational number distance.
- 12. Example 10: Apoint in Q1 and a point in Q4, distance as an irrational number.
- 13. Example 11: Apoint in Q1 and a point in Q4, along a vertical line.
- 14. Example 12: Apoint in Q2 and a point in Q3, whole number distance.
- 15. Example 13: Apoint in Q2 and a point in Q3, distance as an irrational number.
- 16. Example 14: Apoint in Q2 and a point in Q3, along a vertical line.
- 17. Example 15: Apoint in Q3 and a point in Q4, whole number distance.
- 18. Example 16: Apoint in Q3 and a point in Q4, distance as an irrational number.
- 19. Example 17: Apoint in Q3 and a point in Q4, along a horizontal line.
- 20. Example 18: Apoint on the x-axis and point on the y-axis, whole number distance.
- 21. Example 19: Apoint on the x-axis and point on the y-axis, distance as an irrational number.
- 22. Example 20: Apoint on the x-axis and point on the y-axis, along a horizontal line.
- 23. Example 21: Apoint on the x-axis and point on the y-axis, along a vertical line.