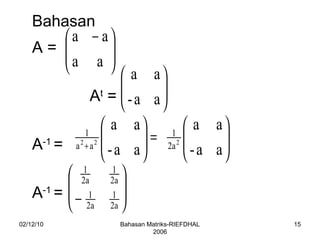
Dokumen ini berisi pembahasan mengenai soal-soal matriks, termasuk cara menentukan nilai-nilai variabel dalam persamaan matriks, serta penggunaan determinan untuk menentukan singularitas matriks. Terdapat juga penjelasan mengenai kondisi matriks tidak memiliki invers dan penyelesaian sistem persamaan matriks. Beberapa contoh soal mencakup perhitungan nilai, titik potong garis, dan hubungan antara elemen-elemen matriks.

1. PEMBAHASAN SOAL-SOAL MATRIKS 02/12/10 Bahasan Matriks-RIEFDHAL 2006

2. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 1. Diketahui persamaan matriks : Tentukan nilai a + b + c + d

3. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 Bahasan:

4. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 3b + 8 = 11 -> 3b = 3 -> b = 1 3a + 2 = b + 4 -> 3a = 5 – 2 3a = 3 -> a = 1 3(a – c) – 3 = - 6 3(1 – c) = -3 1 – c = -1 -> -c = - 2 -> c = 2 3a + 2 = 1 + 4 -1

5. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 b = 1; a = 1; c = 2 3(c + d) + 1 = 16 3(2 + d) = 15 2 + d = 5 -> d = 3 Jadi, a + b + c + d = 1 + 1 + 2 + 3 = 7 5

6. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 2. Jika f(x) = X 2 – 2X dan Maka f(A) = ….

7. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 f(x) = X 2 – 2X dan Maka f(A) = A 2 – 2A = = Bahasan:

8. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 3. Determinan matriks ordo 3 x 3. Jika adalah matriks singular maka nilai x = ….

9. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 Bahasan: Matriks A adalah matriks singular , jika determinan A = 0 2 4 1 3 6 -2 + + _ = 0 0 + 3x + (-40) (-4x) _ _ - 0 = 0 - 30 - + 7x – 70 = 0 -> x = 10

10. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 4. Jika adalah matriks singular dengan demikain nilai x = ….

11. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 Bahasan: Matriks A adalah matriks singular , jika determinan A = 0 2 5 7 3 4 7 + + _ = 0 8x + 126 + (-35) - 84 _ _ - 15x = 0 - (-28) + -7x + 35 = 0 -> x = 5

12. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 5. Matriks tidak mempunyai invers bila a. a dan b sembarang b. a ≠ 0, b ≠ 0 dan a = b c. a ≠ 0, b ≠ 0 dan a = - b d. a = 0 dan b sembarang e. b = 0 dan a sembarang

13. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 Bahasan tidak mempunyai invers jadi determinannya sama dengan nol = 0 (a – b)(a + b) – a 2 = 0 a 2 – b 2 – a 2 = 0 -b 2 = 0 -> b = 0 Jadi, b = 0 dan a sembarang

14. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 6. Diberikan matriks A = Himpunan nilai a yang memenuhi hubungan A -1 = A t (invers A = A transpos) adalah…. a. {√2,√2 } b. {1, -1} c. {½√2, -½√2} d. {½, -½} e. {½√2, -¼√2}

15. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 Bahasan A = A t = A -1 = A -1 =

16. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 A t = dan A -1 = A t = A -1 -> 2a 2 = 1 -> a 2 = ½ a = ±√½ = ±½√2 a 1 = ½√2 dan a 2 = -½√2

17. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 7. Jika maka P =….

18. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 Bahasan: PA = B -> P = B.A -1

19. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 PA = B -> P = B.A -1 P = P =

20. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 P = P = P =

21. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 8. Titik potong dari dua garis yang disajikan sebagai persamaan matriks adalah…. a. (1,-2) b. (-1,2) c. (-1,-2) d. (1,2) e. (2,1)

22. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 Bahasan: A.X = B X = A -1 .B

23. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 -> x = 1 dan y = 2 Jadi titik potongnya (1,2)

24. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 9. Jika maka b =…. a. 1 b. 2 c. 3 d. 4 e. 5

25. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 Bahasan: 10a = 20 -> a = 2

26. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 10a = 20 -> a = 2 -4 + 2a + b = 1 -4 + 4 + b = 1 -> Jadi, b = 1

27. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 10. Diketahui matriks A = dan berlaku hubungan A 2 = pA + qI maka nilai p dan q a. p = 3 dan q = 10 b. p = -3 dan q = 10 c. p = -2 dan q = 9 d. p = 2 dan q = 10 e. p = 10 dan q = -3

28. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 Bahasan: A 2 = pA + qI

29. 02/12/10 Bahasan Matriks-RIEFDHAL 2006 -6 = 2p -> p = -3 7 = p + q 7 = -3 + q -> q = 10 Jadi, p = -3 dan q = 10