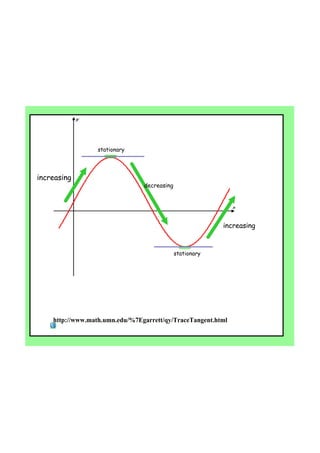
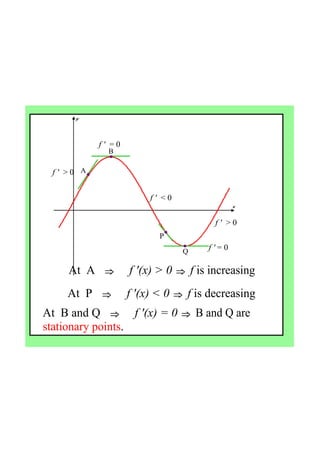
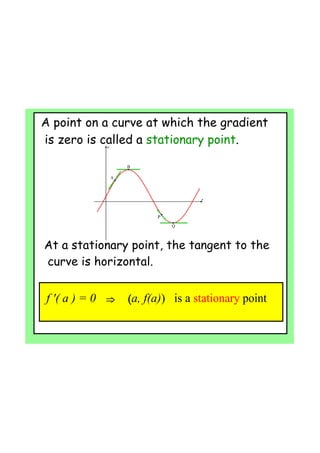
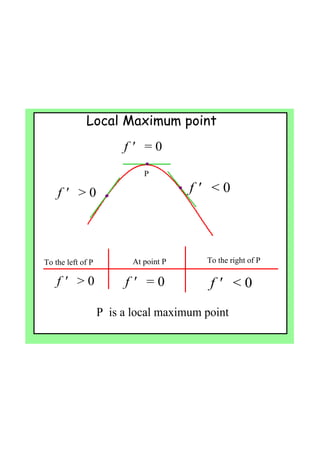
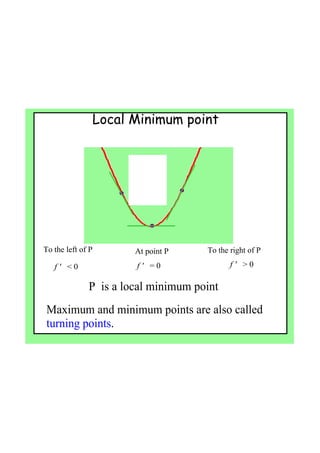
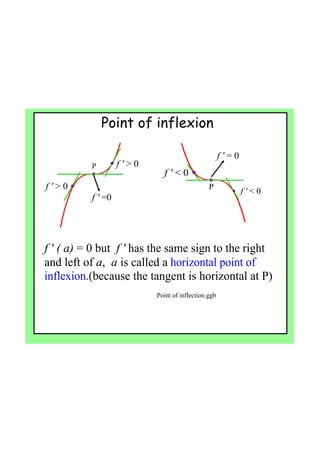
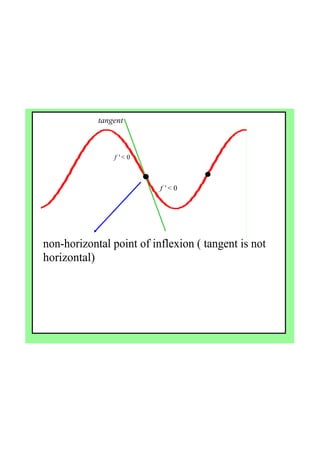
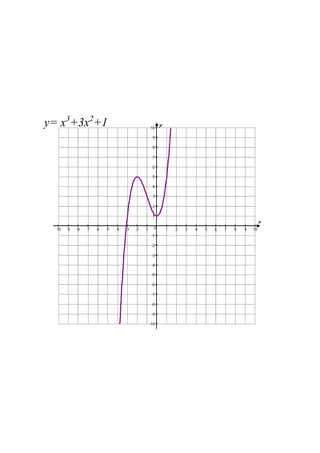
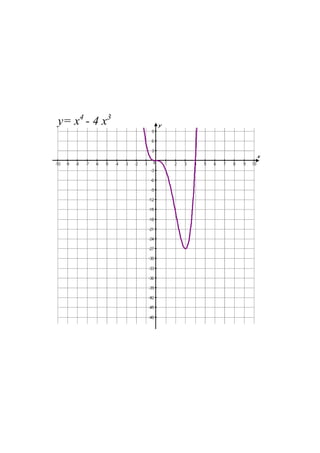
By the end of the lesson, students will be able to use derivatives to find maximum and minimum points of a function, and use second derivatives to determine the nature of stationary points and points of inflection. Specifically, they will learn that: (1) if the first derivative is zero at a point, it is a stationary point; (2) the second derivative test can determine if it is a local max, min or point of inflection; and (3) points of inflection occur when the curve changes concavity. Students will apply these concepts to find the stationary points of sample functions and classify their nature.

1. By the end of the lesson you will be able to:
• Use the derivative of a function to find
maximum and minimum points.
• Use the second derivative to test the nature of a
stationary point and/or point of inflexion.

2. increasing
increasing
decreasing
stationary
stationary
http://www.math.umn.edu/%7Egarrett/qy/TraceTangent.html

3. •
•
•
•
A
B
P
Q
At A ⇒ f '(x) > 0 ⇒ f is increasing
At P ⇒ f '(x) < 0 ⇒ f is decreasing
At B and Q ⇒ f '(x) = 0 ⇒ B and Q are
stationary points.
f ' = 0
f ' < 0
f ' > 0
f ' > 0
f ' = 0

4. If the derivative is positive then the function is
increasing.
If the derivative is negative then the function is
decreasing.

5. f '( a ) = 0 ⇒ (a, f(a)) is a stationary point
•
•
•
•
A
B
P
Q
A point on a curve at which the gradient
is zero is called a stationary point.
At a stationary point, the tangent to the
curve is horizontal.

6. •
•
•
Local Maximum point
f ' > 0
f ' = 0
f ' < 0
P
To the left of P At point P To the right of P
f ' > 0 f ' < 0 f ' = 0
P is a local maximum point

7. Local Minimum point
f ' > 0
f ' = 0
f ' < 0
To the left of P At point P To the right of P
f ' > 0 f ' < 0 f ' = 0
P is a local minimum point
P
•
• •
Maximum and minimum points are also called
turning points.

8. Point of inflexion
•
•
•
f ' =0
f ' > 0
f ' > 0P
•
•
•
f ' = 0
f ' < 0
f ' < 0
P
f ' ( a) = 0 but f ' has the same sign to the right
and left of a, a is called a horizontal point of
inflexion.(because the tangent is horizontal at P)
Point of inflection.ggb

9. •
non­horizontal point of inflexion ( tangent is not
horizontal)
f ' < 0
f ' < 0
tangent
•

10. Find the coordinates of the stationary points on the
curve y= x3
+3x2
+1 and determine their nature.

11. y= x3
+3x2
+1

12. Find the coordinates of the stationary points on the
curve y= x4
­ 4 x3
and determine their nature.

13. y= x4
­ 4 x3

14. Attachments
Point of inflection.ggb