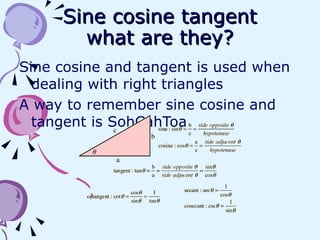
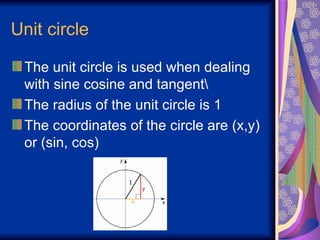
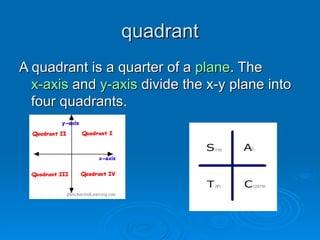
Trigonometry is the study of triangles and angles. It discusses topics like the unit circle, quadrants, trig functions of sine, cosine and tangent, angle measures in degrees and radians, and trig identities. The unit circle is used to find trig function values of angles, with a radius of 1 and coordinates of (x,y) or (sin,cos). A quadrant divides the x-y plane into four sections based on the x and y axes. Trig functions can also be used to convert between degree and radian angle measures using appropriate formulas.

1. trigonometry For dummies by Norma

2. Trigonometry topics discussed Unit circle Quadrants Sine cosine tangent Secant cosecant cotangent Types of angles (initial terminal conterminal reference) Radian and degree measure Pythagorean theorem Trig identities

3. What is trigonometry Trigonometry is the study of triangles and angles

4. Sine cosine tangent what are they? Sine cosine and tangent is used when dealing with right triangles A way to remember sine cosine and tangent is SohCahToa

5. Unit circle The unit circle is used when dealing with sine cosine and tangent\ The radius of the unit circle is 1 The coordinates of the circle are (x,y) or (sin, cos)

6. quadrant A quadrant is a quarter of a plane . The x-axis and y-axis divide the x-y plane into four quadrants.

7. Sine, cosine and tangent measures on the unit circle Angle values for trig

8. Initial and terminal angles reference angle AN ANGLE is in standard position when its vertex A is at the origin of the x-y plane, and its Initial side AB lies along the positive x -axis, while its Terminal side AC has rotated. The reference angle is defined as the acute angle between the terminal side of the given angle and the x axis. The given angle may be in degrees or radians. The reference angle is defined as

9. Convert degrees to radians to convert radians to degrees, multiply by 180 /  , like this: to convert degrees to radians, multiply by    , like this:

10. What are reciprocal trigonometric functions? Reciprocal of trigonometric functions are the opposite of sine cosine and tangent functions Reciprocal of sine is 1 over sine or csc Reciprocal of cosine is 1 over cosine or sec Reciprocal of tangent is 1 over tangent or sin over cos or cot

11. Pythagorean identities Pythagorean identities a)sin² θ + cos² θ = 1 b)1 + tan² θ = sec² θ c)1 + cot² θ = csc ² θ a') sin² θ = 1 − cos² θ . b) cos² θ = 1 − sin² θ .

12. Trig for dummies