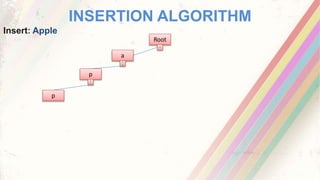
Trie is an efficient data structure for storing and retrieving strings. It stores strings in a tree structure, with each node representing a character. Common operations on a trie like insertion, deletion and searching of strings can be performed in O(M) time where M is the length of the string. The document then provides details on the node structure used to implement a trie, along with pseudocode for inserting strings like "Apple" and "Army" into an empty trie.

1. DATA STRUCTURE
TRIE
Name: Mahadi Hassan
ID: 1320133042
&
Name: Mahmud Rahman Parag
ID: 1320900042

2. What Is TRIE?
Trie Is An Efficient Information Retrieval Data Structure Also Called
Digital Tree And Sometimes Radix Tree Or Prefix Tree (As They Can
Be Searched By Prefixes), Is An Ordered Tree Data Structure That Is
Used To Store A Dynamic Set Or Associative Array Where The Keys
Are Usually Strings.

3. Why Trie Data Structure?
• Searching trees in general favor keys which are of fixed size
since this leads to efficient storage management.
• However in case of applications which are retrieval based and
which call for keys varying length, tries provide better options.
• Tries are also called as Lexicographic Search trees.
• The name trie (pronounced as “try”)originated from the word
“retrieval”.

4. TYPES OF TRIE
1.Standard Tries
2.Compressed Tries
3.Suffix Tries

5. STANDARD TRIE
The Standard Trie For A Set Of Strings S Is An Ordered Tree Such That:
Each Node Labeled With A Character (Without Root).
The Children Of A Node Are Alphabetically Ordered.
The Paths From The External Nodes To The Root Yield The Strings Of S

6. EXAMPLE:
Standard Trie For A Set Of Strings S
S = { bear, bell, bid, bull, buy, sell, stock, stop }

7. TIME COMPLEXITY
A Standard Trie Uses O(n) Space. Operations (find, insert, remove) Take Time
O(dm) Each, Where:
n = Total Size Of The Strings In S,
m = Size Of The String Parameter Of The Operation
d = Alphabet Size

8. TRIE SPECIFICATION
Operations:
addWord
Function Adds word to an .
Postcondition Trie is not full
searchWord
Function Search a word in the trie
Postcondition Returns true if the world is found and false otherwise.
deleteWord
Function Delete a word in the trie
Postcondition Trie is not empty

9. TRIE SPECIFICATION
Operations:
print
Function Print the word in the trie
Postcondition Trie either maybe full or not

10. NODE STRUCTURE
Class Node
{
public:
char value;
bool end;
Node *children[26];
}
The Character Value (A – Z) / (a – z).
Indicates Whether This Node Completes A Word
Represents The 26 Letters In The Alphabet

11. NODE STRUCTURE
char value
bool end
0 1 2 3 4 5 6 7 8 9
1
0
1
1
1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
2
1
2
2
2
3
2
4
2
5
Character
Data
Boolean
Data
A Node Type
Pointer
Array
0

12. INSERTION

13. INSERTION ALGORITHM
Insert: Apple
First Create A Root That Has Empty String And Every Single Pointer Array
Must Point To The NULL (Default). And Boolean Value Of Every Node Must Be
false By Default.
false
0 …
1
0
…
2
0
…
2
6
NULL

14. INSERTION ALGORITHM
Insert: Apple
Root

15. INSERTION ALGORITHM
Insert: Apple
Second Convert All Of The String’s Character To Uppercase Or To Lowercase.
char currentChar = tolower(word.at(i));

16. INSERTION ALGORITHM
Insert: Apple
Second Convert All Of The String’s Character To Uppercase Or To Lowercase.
char currentChar = tolower(word.at(i));
Here, Suppose string s = “Apple” And Length Of String Is 5 So……….

17. INSERTION ALGORITHM
Insert: Apple
Second Convert All Of The String’s Character To Uppercase Or To Lowercase.
char currentChar = tolower(word.at(i));
Here, Suppose string s = “Apple” And Length Of String Is 5 So……….
s[0] = A, s[1] = p, s[2] = p, s[3] = l, s[4] = e

18. INSERTION ALGORITHM
Insert: Apple
Second Convert All Of The String’s Character To Uppercase Or To Lowercase.
char currentChar = tolower(word.at(i));
A p p l e
0 1 2 3 4
Here, Suppose string s = “Apple” And Length Of String Is 5 So……….
s[0] = A, s[1] = p, s[2] = p, s[3] = l, s[4] = e

19. INSERTION ALGORITHM
Insert: Apple
A p p l e
0 1 2 3 4

20. INSERTION ALGORITHM
Insert: Apple
A p p l e
0 1 2 3 4
char currentChar = tolower(word.at(0));
currentChar a

21. INSERTION ALGORITHM
Insert: Apple
Then Get The Correct Index For The Appropriate Character
int index = currentChar - 'a';
So……….
currentChar a
int index = currentChar - 'a'; int index = a - 'a';
int index = 0;

22. INSERTION ALGORITHM
Insert: Apple
Declare A Pointer Node Type Pointer Variable That Point To The Root
Node *currentNode = root;
RootcurrentNode
Pointing To

23. INSERTION ALGORITHM
Insert: Apple
Root
currentNode

24. INSERTION ALGORITHM
Insert: Apple
if (currentNode->children[0] != NULL)
{
currentNode = currentNode->children[0];
}
false
0 …
1
0
…
2
0
…
2
6
NULL
If 0 Pointing To The NULL?
Check If The Current Node Has The Current Character As One Of Its
Descendants

25. INSERTION ALGORITHM
Insert: Apple
if (currentNode->children[0] != NULL)
{
currentNode = currentNode->children[0];
}
Is 0 Pointing To The NULL?
YES!
So IF Statement Won’t Execute…………
And The Current Node Doesn't have the current
character as one of its descendants
Here 0 Is The Index Value ( a – ‘a’ )
Check If The Current Node Has The Current Character As One Of Its
Descendants
false
0 …
1
0
…
2
0
…
2
6
NULL

26. INSERTION ALGORITHM
Insert: Apple
else
{
Node *newNode = new Node(currentChar);
currentNode->children[0] = newNode;
currentNode = newNode;
}
So………. Node Constructor

27. INSERTION ALGORITHM
Insert: Apple
Node *newNode = new Node(currentChar);
So……….
currentChar a
Node(curre
ntChar)

28. INSERTION ALGORITHM
Insert: Apple
Node *newNode = new Node(currentChar);
So……….
currentChar a
aNode(curre
ntChar)

29. INSERTION ALGORITHM
Insert: Apple
Node *newNode = new Node(currentChar);
So……….
currentChar a
aNode(curre
ntChar)
anewNode
All 26 Children Of newNode Will Point To The NULL

30. INSERTION ALGORITHM
Insert: Apple
currentNode->children[0] = newNode;
So……….
anewNode RootcurrentNode
0

31. INSERTION ALGORITHM
Insert: Apple
currentNode->children[0] = newNode;
So……….
a
newNode Root
0
currentNode

32. INSERTION ALGORITHM
Insert: Apple
currentNode = newNode;
So……….
a
newNode Root
0
currentNode

33. INSERTION ALGORITHM
Insert: Apple
if (i == word.size() - 1)
{
currentNode->end = true;
}
Now Check If It Is The Last Character Of The Word Has Been Reached
0 == 4? NO  Won’t Execute

34. INSERTION ALGORITHM
Insert: Apple
So……….
a
newNode Root
0
currentNode
bool end will be false

35. INSERTION ALGORITHM
Insert: Apple
Root
0
acurrentNode

36. INSERTION ALGORITHM
Insert: Apple
A p p l e
0 1 2 3 4
char currentChar = tolower(word.at(1));
currentChar p

37. INSERTION ALGORITHM
Insert: Apple
Then Get The Correct Index For The Appropriate Character
int index = currentChar - 'a';
So……….
currentChar p
int index = currentChar - 'a'; int index = p - 'a';
int index = 15;

38. INSERTION ALGORITHM
Insert: Apple
if (currentNode->children[15] != NULL)
{
currentNode = currentNode->children[15];
}
a
false
1
5
…
1
0
…
2
0
…
2
6
NULL
If 15 Pointing To The NULL?
Check If The Current Node Has The Current Character As One Of Its
Descendants

39. INSERTION ALGORITHM
Insert: Apple
if (currentNode->children[15] != NULL)
{
currentNode = currentNode->children[15];
}
Check If The Current Node Has The Current Character As One Of Its
Descendants
a
false
1
5
…
1
0
…
2
0
…
2
6
Is 15 Pointing To The NULL?
YES!
So IF Statement Won’t Execute…………
And The Current Node Doesn't have the current
character as one of its descendants
Here 15 Is The Index Value ( p – ‘a’ )
NULL

40. INSERTION ALGORITHM
Insert: Apple
else
{
Node *newNode = new Node(currentChar);
currentNode->children[15] = newNode;
currentNode = newNode;
}
So………. Node Constructor

41. INSERTION ALGORITHM
Insert: Apple
Node *newNode = new Node(currentChar);
So……….
currentChar p
Node(curre
ntChar)

42. INSERTION ALGORITHM
Insert: Apple
Node *newNode = new Node(currentChar);
So……….
currentChar p
pNode(curre
ntChar)

43. INSERTION ALGORITHM
Insert: Apple
Node *newNode = new Node(currentChar);
So……….
currentChar p
pNode(curre
ntChar)
pnewNode
All 26 Children Of newNode Will Point To The NULL

44. INSERTION ALGORITHM
Insert: Apple
currentNode->children[15] = newNode;
So……….
pnewNode acurrentNode
1
5

45. INSERTION ALGORITHM
Insert: Apple
currentNode->children[15] = newNode;
So……….
p
newNode a
1
5
currentNode

46. INSERTION ALGORITHM
Insert: Apple
currentNode = newNode;
So……….
p
newNode a
1
5
currentNode

47. INSERTION ALGORITHM
Insert: Apple
if (i == word.size() - 1)
{
currentNode->end = true;
}
Now Check If It Is The Last Character Of The Word Has Been Reached
1 == 4? NO  Won’t Execute

48. INSERTION ALGORITHM
Insert: Apple
So……….
p
newNode a
1
5
currentNode
bool end will be false

49. INSERTION ALGORITHM
Insert: Apple
Root
0
a
1
5
p
currentNode

50. INSERTION ALGORITHM
Insert: Apple
SIMILARLY

51. INSERTION ALGORITHM
Insert: Apple
Root
0
a
1
5
p
1
5
p

52. INSERTION ALGORITHM
Insert: Apple
Root
0
a
1
5
p
1
5
p
1
1
l

53. INSERTION ALGORITHM
Insert: Apple
Root
0
a
1
5
p
1
5
p
1
1
l
4
e

54. INSERTION ALGORITHM
Insert: Apple
if (i == word.size() - 1)
{
currentNode->end = true;
}
Now Check If It Is The Last Character Of The Word Has Been Reached
4 == 4? YES  Will Execute

55. INSERTION ALGORITHM
Insert: Apple
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True

56. INSERTION ALGORITHM
Now Insert: Army

57. INSERTION ALGORITHM
Insert: Army
A r m y
0 1 2 3

58. INSERTION ALGORITHM
Insert: Army
A r m y
0 1 2 3
char currentChar = tolower(word.at(0));
currentChar a

59. INSERTION ALGORITHM
Insert: Army
Then Get The Correct Index For The Appropriate Character
int index = currentChar - 'a';
So……….
currentChar a
int index = currentChar - 'a'; int index = a - 'a';
int index = 0;

60. INSERTION ALGORITHM
Insert: Army
Declare A Pointer Node Type Pointer Variable That Point To The Root
Node *currentNode = root;
RootcurrentNode
Pointing To

61. DELETE ALGORITHM
Delete: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
currentNode

62. INSERTION ALGORITHM
Insert: Army
if (currentNode->children[0] != NULL)
{
currentNode = currentNode->children[0];
}
false
0 …
1
0
…
2
0
…
2
6
NULL
If 0 Pointing To The NULL?
Check If The Current Node Has The Current Character As One Of Its
Descendants

63. INSERTION ALGORITHM
Insert: Army
if (currentNode->children[0] != NULL)
{
currentNode = currentNode->children[0];
}
Is 0 Pointing To The NULL?
NO!
So IF Statement Will Execute…………
Here 0 Is The Index Value ( a – ‘a’ )
Check If The Current Node Has The Current Character As One Of Its
Descendants
false
0 …
1
0
…
2
0
…
2
6
NULL

64. INSERTION ALGORITHM
Insert: Army
currentNode = currentNode->children[0];
So……….

65. INSERTION ALGORITHM
Insert: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
currentNode
bool end will be True

66. INSERTION ALGORITHM
Insert: Army
if (i == word.size() - 1)
{
currentNode->end = true;
}
Now Check If It Is The Last Character Of The Word Has Been Reached
0 == 3? NO  Won’t Execute

67. INSERTION ALGORITHM
Insert: Army
A r m y
0 1 2 3
char currentChar = tolower(word.at(1));
currentChar r

68. INSERTION ALGORITHM
Insert: Army
Then Get The Correct Index For The Appropriate Character
int index = currentChar - 'a';
So……….
currentChar r
int index = currentChar - 'a'; int index = r - 'a';
int index = 17;

69. INSERTION ALGORITHM
Insert: Army
if (currentNode->children[17] != NULL)
{
currentNode = currentNode->children[17];
}
a
false
1
7
…
1
0
…
2
0
…
2
6
NULL
If 15 Pointing To The NULL?
Check If The Current Node Has The Current Character As One Of Its
Descendants

70. INSERTION ALGORITHM
Insert: Army
if (currentNode->children[17] != NULL)
{
currentNode = currentNode->children[17];
}
Check If The Current Node Has The Current Character As One Of Its
Descendants
a
false
1
7
…
1
0
…
2
0
…
2
6
Is 17 Pointing To The NULL?
YES!
So IF Statement Won’t Execute…………
And The Current Node Doesn't have the current
character as one of its descendants
Here 17 Is The Index Value ( r – ‘a’ )
NULL

71. INSERTION ALGORITHM
Insert: Army
else
{
Node *newNode = new Node(currentChar);
currentNode->children[17] = newNode;
currentNode = newNode;
}
So………. Node Constructor

72. INSERTION ALGORITHM
Insert: Army
Node *newNode = new Node(currentChar);
So……….
currentChar r
Node(curre
ntChar)

73. INSERTION ALGORITHM
Insert: Army
Node *newNode = new Node(currentChar);
So……….
currentChar r
rNode(curre
ntChar)

74. INSERTION ALGORITHM
Insert: Army
Node *newNode = new Node(currentChar);
So……….
currentChar r
rNode(curre
ntChar)
rnewNode
All 26 Children Of newNode Will Point To The NULL

75. INSERTION ALGORITHM
Insert: Army
currentNode->children[17] = newNode;
So……….

76. INSERTION ALGORITHM
Insert: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
currentNode

77. INSERTION ALGORITHM
Insert: Army
currentNode = newNode;
So……….

78. INSERTION ALGORITHM
Insert: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
currentNode

79. INSERTION ALGORITHM
Insert: Army
if (i == word.size() - 1)
{
currentNode->end = true;
}
Now Check If It Is The Last Character Of The Word Has Been Reached
1 == 3? NO  Won’t Execute

80. INSERTION ALGORITHM
Insert: Army
SIMILARLY

81. INSERTION ALGORITHM
Insert: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5

82. INSERTION ALGORITHM
Insert: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y

83. INSERTION ALGORITHM
Insert: Army
if (i == word.size() - 1)
{
currentNode->end = true;
}
Now Check If It Is The Last Character Of The Word Has Been Reached
3 == 3? YES  Will Execute

84. INSERTION ALGORITHM
Insert: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y

85. DELETION

86. DELETION ALGORITHM
Delete: Army
A r m y
0 1 2 3
char currentChar = tolower(word.at(0));
currentChar a

87. DELETION ALGORITHM
Delete: Army
Then Get The Correct Index For The Appropriate Character
int index = currentChar - 'a';
So……….
currentChar a
int index = currentChar - 'a'; int index = a - 'a';
int index = 0;

88. DELETION ALGORITHM
Delete: Army
Declare A Pointer Node Type Pointer Variable That Point To The Root
Node *currentNode = root;
RootcurrentNode
Pointing To

89. DELETION ALGORITHM
Delete: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
currentNode

90. DELETION ALGORITHM
Delete: Army
if (currentNode->children[0] != NULL)
{
currentNode = currentNode->children[0];
}
false
0 …
1
0
…
2
0
…
2
6
NULL
If 0 Pointing To The NULL?
Check If The Current Node Has The Current Character As One Of Its
Descendants

91. DELETION ALGORITHM
Delete: Army
if (currentNode->children[0] != NULL)
{
currentNode = currentNode->children[0];
}
Is 0 Pointing To The NULL?
NO!
So IF Statement Will Execute…………
Here 0 Is The Index Value ( a – ‘a’ )
Check If The Current Node Has The Current Character As One Of Its
Descendants
false
0 …
1
0
…
2
0
…
2
6
NULL

92. DELETION ALGORITHM
Delete: Army
currentNode = currentNode->children[0];
So……….

93. DELETION ALGORITHM
Delete: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
currentNode

94. DELETION ALGORITHM
Delete: Army
A r m y
0 1 2 3
char currentChar = tolower(word.at(1));
currentChar r

95. DELETION ALGORITHM
Delete: Army
Then Get The Correct Index For The Appropriate Character
int index = currentChar - 'a';
So……….
currentChar r
int index = currentChar - 'a'; int index = r - 'a';
int index = 17;

96. DELETION ALGORITHM
Delete: Army
if (currentNode->children[17] != NULL)
{
currentNode = currentNode->children[17];
}
a
false
1
7
…
1
0
…
2
0
…
2
6
NULL
If 15 Pointing To The NULL?
Check If The Current Node Has The Current Character As One Of Its
Descendants

97. DELETION ALGORITHM
Delete: Army
if (currentNode->children[17] != NULL)
{
currentNode = currentNode->children[17];
}
Check If The Current Node Has The Current Character As One Of Its
Descendants
a
false
1
7
…
1
0
…
2
0
…
2
6
Is 17 Pointing To The NULL?
NO!
So IF Statement Will Execute…………
Here 17 Is The Index Value ( r – ‘a’ )
NULL

98. DELETION ALGORITHM
Delete: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
currentNode

99. DELETION ALGORITHM
Delete: Army
SIMILARLY

100. DELETION ALGORITHM
Delete: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
currentNode

101. DELETION ALGORITHM
Delete: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
currentNode

102. DELETION ALGORITHM
Delete: Army
if (i == word.size() – 1 && currentNode->end)
{
currentNode->end = false;
}
Now Check If It Is The Last Character Of The Word Has Been Reached
3 == 3? && currentNode  end? YES  Will Execute

103. DELETION ALGORITHM
Delete: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
bool end will be False So Word Couldn’t
Be Found By Search So The Word Is
Deleted.

104. SEARCH

105. SEARCHING ALGORITHM
Search: Army
A r m y
0 1 2 3
char currentChar = tolower(word.at(0));
currentChar a

106. SEARCHING ALGORITHM
SEARCH: Army
Then Get The Correct Index For The Appropriate Character
int index = currentChar - 'a';
So……….
currentChar a
int index = currentChar - 'a'; int index = a - 'a';
int index = 0;

107. SEARCHING ALGORITHM
Search: Army
Declare A Pointer Node Type Pointer Variable That Point To The Root
Node *currentNode = root;
RootcurrentNode
Pointing To

108. SEARCHING ALGORITHM
Search: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
currentNode

109. SEARCHING ALGORITHM
Search: Army
if (currentNode->children[0] != NULL)
{
currentNode = currentNode->children[0];
}
false
0 …
1
0
…
2
0
…
2
6
NULL
If 0 Pointing To The NULL?
Check If The Current Node Has The Current Character As One Of Its
Descendants

110. SEARCHING ALGORITHM
Search: Army
if (currentNode->children[0] != NULL)
{
currentNode = currentNode->children[0];
}
Is 0 Pointing To The NULL?
NO!
So IF Statement Will Execute…………
Here 0 Is The Index Value ( a – ‘a’ )
Check If The Current Node Has The Current Character As One Of Its
Descendants
false
0 …
1
0
…
2
0
…
2
6
NULL

111. SEARCHING ALGORITHM
Search: Army
currentNode = currentNode->children[0];
So……….

112. SEARCHING ALGORITHM
Search: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
currentNode

113. SEARCHING ALGORITHM
Search: Army
A r m y
0 1 2 3
char currentChar = tolower(word.at(1));
currentChar r

114. SEARCHING ALGORITHM
Search: Army
Then Get The Correct Index For The Appropriate Character
int index = currentChar - 'a';
So……….
currentChar r
int index = currentChar - 'a'; int index = r - 'a';
int index = 17;

115. SEARCHING ALGORITHM
Search: Army
if (currentNode->children[17] != NULL)
{
currentNode = currentNode->children[17];
}
a
false
1
7
…
1
0
…
2
0
…
2
6
NULL
If 15 Pointing To The NULL?
Check If The Current Node Has The Current Character As One Of Its
Descendants

116. SEARCHING ALGORITHM
Search: Army
if (currentNode->children[17] != NULL)
{
currentNode = currentNode->children[17];
}
Check If The Current Node Has The Current Character As One Of Its
Descendants
a
false
1
7
…
1
0
…
2
0
…
2
6
Is 17 Pointing To The NULL?
NO!
So IF Statement Will Execute…………
Here 17 Is The Index Value ( r – ‘a’ )
NULL

117. SEARCHING ALGORITHM
Search: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
currentNode

118. SEARCHING ALGORITHM
Search: Army
SIMILARLY

119. SEARCHING ALGORITHM
Search: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
currentNode

120. SEARCHING ALGORITHM
Search: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
currentNode

121. SEARCHING ALGORITHM
Search: Army
if (i == word.size() – 1 && currentNode->end)
{
return true;
}
Now Check If It Is The Last Character Of The Word Has Been Reached
3 == 3? && currentNode  end? YES  Will Execute

122. SEARCHING ALGORITHM
Search: Army
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
Return True. Item Found !

123. PRINTING WORD

124. PRINTING ALGORITHM
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y

125. PRINTING ALGORITHM
Trie::alphabetize(Node * node, string prefix = "")
{
if (node->end)
cout << prefix << endl;
for (int i = 0; i < 26; ++i)
{
if (node->children[i] != NULL)
{
string currentString = prefix + node->children[i]->value;
alphabetize(node->children[i], currentString);
}
}
}

126. PRINTING ALGORITHM
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
if (node->end) (1)

127. PRINTING ALGORITHM
Printing Result
CASE RESULT
CASE 1 FALSE

128. PRINTING ALGORITHM
Trie::alphabetize(Node * node, string prefix = "")
{
if (node->end)
cout << prefix << endl;
for (int i = 0; i < 26; ++i)
{
if (node->children[i] != NULL)
{
string currentString = prefix + node->children[i]->value;
alphabetize(node->children[i], currentString);
}
}
}

129. PRINTING ALGORITHM
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
if (node->children[0] != NULL) (2)

130. PRINTING ALGORITHM
Printing Result
CASE RESULT
CASE 1 FALSE
CASE 2 TRUE
string currentString = prefix + node->children[0]->value;
string currentString = “” +a;
string currentString = a;
alphabetize(node->children[0], currentString);

131. PRINTING ALGORITHM
Trie::alphabetize(Node * node, string prefix = "")
{
if (node->end)
cout << prefix << endl;
for (int i = 0; i < 26; ++i)
{
if (node->children[i] != NULL)
{
string currentString = prefix + node->children[i]->value;
alphabetize(node->children[i], currentString);
}
}
}

132. PRINTING ALGORITHM
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
if (node->children[1] != NULL) (3)

133. PRINTING ALGORITHM
Printing Result
CASE RESULT
CASE 3 FALSE

134. PRINTING ALGORITHM
Trie::alphabetize(Node * node, string prefix = "")
{
if (node->end)
cout << prefix << endl;
for (int i = 0; i < 26; ++i)
{
if (node->children[i] != NULL)
{
string currentString = prefix + node->children[i]->value;
alphabetize(node->children[i], currentString);
}
}
}

135. PRINTING ALGORITHM
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
if (node->children[2] != NULL) (4)

136. PRINTING ALGORITHM
Printing Result
CASE RESULT
CASE 4 FALSE

137. PRINTING ALGORITHM
Trie::alphabetize(Node * node, string prefix = "")
{
if (node->end)
cout << prefix << endl;
for (int i = 0; i < 26; ++i)
{
if (node->children[i] != NULL)
{
string currentString = prefix + node->children[i]->value;
alphabetize(node->children[i], currentString);
}
}
}

138. PRINTING ALGORITHM
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
if (node->children[15] != NULL)
(17)

139. PRINTING ALGORITHM
Printing Result
CASE RESULT
CASE 17 TRUE
string currentString = prefix + node->children[15]->value;
string currentString = a + p;
string currentString = ap;
alphabetize(node->children[15], currentString);

140. PRINTING ALGORITHM
Trie::alphabetize(Node * node, string prefix = "")
{
if (node->end)
cout << prefix << endl;
for (int i = 0; i < 26; ++i)
{
if (node->children[i] != NULL)
{
string currentString = prefix + node->children[i]->value;
alphabetize(node->children[i], currentString);
}
}
}

141. PRINTING ALGORITHM
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
if (node->children[15] != NULL)
(18)

142. PRINTING ALGORITHM
Printing Result
CASE RESULT
CASE 18 TRUE
string currentString = prefix + node->children[15]->value;
string currentString = ap + p;
string currentString = app;
alphabetize(node->children[15], currentString);

143. PRINTING ALGORITHM
SIMILARLY

144. PRINTING ALGORITHM
Trie::alphabetize(Node * node, string prefix = "")
{
if (node->end)
cout << prefix << endl;
for (int i = 0; i < 26; ++i)
{
if (node->children[i] != NULL)
{
string currentString = prefix + node->children[i]->value;
alphabetize(node->children[i], currentString);
}
}
}

145. PRINTING ALGORITHM
Root
0
a
1
5
p
1
5
p
1
1
l
4
e
bool end will be True
1
7
r
1
2
m
1
5
y
if (node->children[4] != NULL)
(19)

146. PRINTING ALGORITHM
Trie::alphabetize(Node * node, string prefix = "")
{
if (node->end)
cout << prefix << endl;
for (int i = 0; i < 26; ++i)
{
if (node->children[i] != NULL)
{
string currentString = prefix + node->children[i]->value;
alphabetize(node->children[i], currentString);
}
}
}

147. PRINTING ALGORITHM
Printing Result
CASE RESULT
CASE 19 TRUE
string currentString = prefix + node->children[15]->value;
string currentString = appl + e;
string currentString = apple;
alphabetize(node->children[4], currentString);

148. PRINTING ALGORITHM
Printing Result
Print  apple

149. PRINTING ALGORITHM
SIMILARLY

150. PRINTING ALGORITHM
Printing Result
Print  apple
Print  army

151. SOURCE CODETrie.h
#ifndef TRIE_H
#define TRIE_H
#include <iostream>
#include <vector>
#include <string>
#include <assert.h>
#include <new>
using namespace std;
class Node
{
public:
char value;
bool end;
Node *children[26];
Node(char value);
};
class Trie
{
public:
Trie();
void addWord(string word);
bool searchForWord(string word);
void deleteWord(string word);
Node *getRoot();
void alphabetize(Node *, string);
private:
Node *root;
};
#endif // TRIE_H

152. SOURCE CODETrie.c
#ifndef TRIE_CPP
#define TRIE_CPP
#include <iostream>
#include "trie.h"
using namespace std;
Node::Node(char value)
{
this->value = value;
end = false;
for(int i = 0; i < 26; ++i)
{
children[i] = NULL;
}
}
Trie::Trie()
{
root = new Node(' ');
root->end = true;
}
Node *Trie::getRoot()
{
return root;
}

153. SOURCE CODETrie.c
void Trie::addWord(string word)
{
Node * currentNode = root;
for (int i = 0; i < (int)word.size(); ++i)
{
char currentChar = tolower(word.at(i));
int index = currentChar - 'a';
assert(index >= 0); // Makes sure the character is between a-z
if (currentNode->children[index] != NULL)
{
// check if the current node has the current character as one of its
decendants
currentNode = currentNode->children[index];
}
else
{
// the current node doesn't have the current character as one of its
decendants
Node * newNode = new Node(currentChar);
currentNode->children[index] = newNode;
currentNode = newNode;
}
if (i == (int)word.size() - 1)
{
// the last character of the word has been reached
currentNode->end = true;
}
}
}

154. SOURCE CODETrie.c
bool Trie::searchForWord(string word)
{
Node *currentNode = root;
for(int i = 0; i < (int)word.size(); ++i)
{
char currentChar = tolower(word.at(i));
int index = currentChar - 'a';
assert(index >= 0);
if(currentNode->children[index] != NULL)
{
currentNode = currentNode->children[index];
}
else
{
return false;
}
if(i == (int)word.size() - 1 && !currentNode->end)
{
return false;
}
}
return true;
}

155. SOURCE CODETrie.c
void Trie::deleteWord(string word)
{
Node *currentNode = root;
for(int i = 0; i < (int)word.size(); ++i)
{
char currentChar = tolower(word.at(i));
int index = currentChar - 'a';
assert(index >= 0);
if(currentNode->children[index] != NULL)
{
currentNode = currentNode->children[index];
}
else
{
return;
}
if(i == (int)word.size() - 1 && currentNode->end)
{
currentNode->end = false;
}
}
}

156. SOURCE CODETrie.c
void Trie::alphabetize(Node *node, string prefix = "")
{
if (node->end)
cout << prefix << endl;
for (int i = 0; i < 26; ++i)
{
if (node->children[i] != NULL)
{
string currentString = prefix + node->children[i]->value;
alphabetize(node->children[i], currentString);
}
}
}
#endif // TRIE_CPP

157. SOURCE CODEMain.cpp
#include <iostream>
#include “trie.h”
using namespace std;
int main()
{
Trie * t = new Trie();
t->addWord("Carlos");
t->addWord("Perea");
t->addWord("Hello");
t->addWord("Ball");
t->addWord("Balloon");
t->addWord("Show");
t->addWord("Shower");
t->alphabetize(t->getRoot(), "");
t-> alphabetize(t->getRoot(), "");
return 0;
}

158. OUTPUT

159. APPLICATIONS OF TRIE DATA
STRUCTURES

160. TRIES IN AUTO COMPLETE
• Since a trie is a tree-like data structure in which each node
contains an array of pointers, one pointer for each character in the
alphabet.
• Starting at the root node, we can trace a word by following
pointers corresponding to the letters in the target word.
• Starting from the root node, you can check if a word exists in the
trie easily by following pointers corresponding to the letters in the

161. TRIES IN AUTO COMPLETE
• Auto-complete functionality is used widely over the internet and
mobile apps. A lot of websites and apps try to complete your input
as soon as you start typing.
• All the descendants of a node have a common prefix of the string
associated with that node.

162. TRIES IN AUTO COMPLETE

163. AUTO COMPLETE IN GOOGLE SEARCH

164. WHY TRIES IN AUTO COMPLETE
• Implementing auto complete using a trie is easy.
• We simply trace pointers to get to a node that represents the string
the user entered. By exploring the trie from that node down, we
can enumerate all strings that complete user’s input.

165. AUTOMATIC COMMAND COMPLETION
• When using an operating system such as Unix or DOS, we type in
system commands to accomplish certain tasks. For example, the
Unix and DOS command cd may be used to change the current
directory.

166. SPELL CHECKERS

167. PHONE BOOK SEARCH

168. THANKS TO EVRYONE