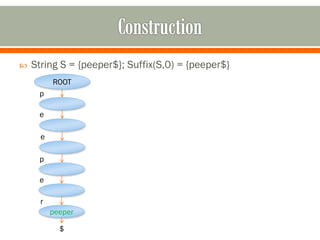
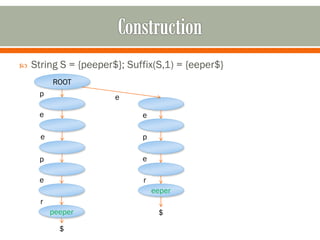
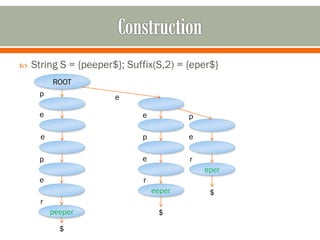
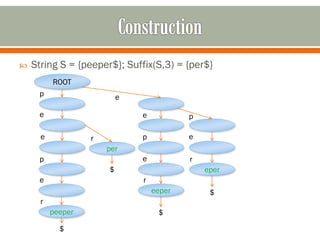
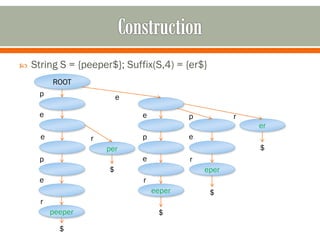
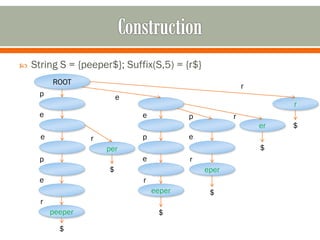
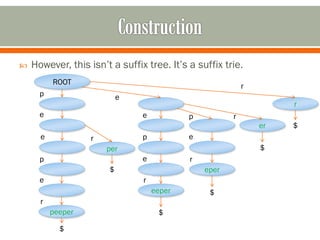
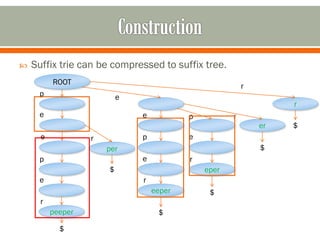
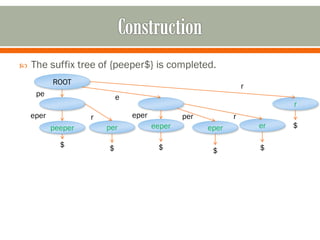
This document discusses suffix trees, including their definition, important contributors, construction, implementation, and applications. Key points: - A suffix tree is a compressed trie representing all suffixes of a string. It allows efficient pattern matching in linear time. - Important contributors include Weiner (1973), McCreight (1976), Ukkonen (1995), and Farach (1997) who developed faster construction algorithms. 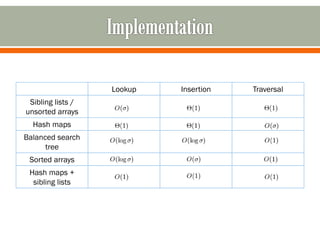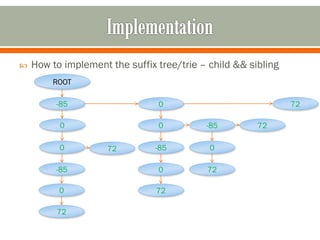- There are multiple ways to implement a suffix tree, including using sibling lists, hash maps, balanced search trees, or sorted arrays. External memory may be needed for very large trees. - Applications include fast substring search, longest common substring problems, and data compression. References provide more details on

1.  
pig.sh
120816

2.  Abstract
 Construction
 Implementation
 Reference

3.  Alias: position tree, PAT tree
 Important people
o Weiner (1973) first introduction
o McCreight (1976) simplified the construction
o Ukkonen (1995) fastest construction algorithm
o Farach (1997) optimal construction algorithm for all alphabets

4.  Trie
 string: S, length: N
 Suffix tree of S:
o the paths from the root to the leaves have a one-to-one relationship
with the suffixes of S.
o edges spell non-empty strings.
o all internal nodes (except perhaps the root) have at least two
children
-- reference. Wikipedia. Suffix tree

5.  String S = {peeper$}; Suffix(S,0) = {peeper$}
ROOT
p
e
e
p
e
r
peeper
$

6.  String S = {peeper$}; Suffix(S,1) = {eeper$}
ROOT
p e
e e
e p
p e
e r
eeper
r
peeper $
$

7.  String S = {peeper$}; Suffix(S,2) = {eper$}
ROOT
p e
e e p
e p e
p e r
eper
e r
eeper $
r
peeper $
$

8.  String S = {peeper$}; Suffix(S,3) = {per$}
ROOT
p e
e e p
e r p e
per
p e r
$ eper
e r
eeper $
r
peeper $
$

9.  String S = {peeper$}; Suffix(S,4) = {er$}
ROOT
p e
e e p r
er
e r p e
per $
p e r
$ eper
e r
eeper $
r
peeper $
$

10.  String S = {peeper$}; Suffix(S,5) = {r$}
ROOT
r
p e
r
e e p r
er $
e r p e
per $
p e r
$ eper
e r
eeper $
r
peeper $
$

11.  However, this isn’t a suffix tree. It’s a suffix trie.
ROOT
r
p e
r
e e p r
er $
e r p e
per $
p e r
$ eper
e r
eeper $
r
peeper $
$

12.  Suffix trie can be compressed to suffix tree.
ROOT
r
p e
r
e e p r
er $
e r p e
per $
p e r
$ eper
e r
eeper $
r
peeper $
$

13.  The suffix tree of {peeper$} is completed.
ROOT
r
pe e
r
eper r eper per r
peeper per eeper eper er $
$ $ $ $
$

14.  There are many ways to implement suffix tree.
o Sibling lists / unsorted arrays
o Hash maps
o Balanced search tree
o Sorted array
o Hash maps + sibling lists

15. Lookup Insertion Traversal
Sibling lists /
unsorted arrays
Hash maps
Balanced search
tree
Sorted arrays
Hash maps +
sibling lists

16.  How to implement the suffix tree/trie – child && sibling
ROOT
-85 0 72
0 0 -85 72
0 72 -85 0
-85 0 72
0 72
72

17.  struct node{
struct node *child, *sibling;
int c_num, s_num;
int slope;
int node_type;
char *obslist_file;
}
 node_type is used to indicate what the node is.
(root / inter-node / leaf / terminal)
 obslist_file is used for external memory.
The data that seldom queried will be recorded in this file.

18.  If the trie is too big, how can I do?
o If trie is constructed by C-S-Link, every subtree is a binary tree.
o Record the in-order and pre-/post- order sequence.
o Use two sequence to reconstruct, if we want to query the subtree.

19.  Wikipedia – suffix tree
http://en.wikipedia.org/wiki/Suffix_tree
 Data Structures, Algorithms, & Applications in Java Suffix Trees
Copyright 1999 Sartaj Sahni
http://www.cise.ufl.edu/~sahni/dsaaj/enrich/c16/suffix.htm#tree
 Websites for suffix tree/trie
o http://blog.csdn.net/ljsspace/article/details/6581850
o http://www.allisons.org/ll/AlgDS/Tree/Suffix/
o http://blog.csdn.net/TsengYuen/article/details/4815921
o http://www.cppblog.com/yuyang7/archive/2009/03/29/78252.html