Downloaded 64 times
Uploaded byEva Lantsoght
Effective Width in Shear of Reinforced Concrete Solid Slab Bridges under Wheel Loads
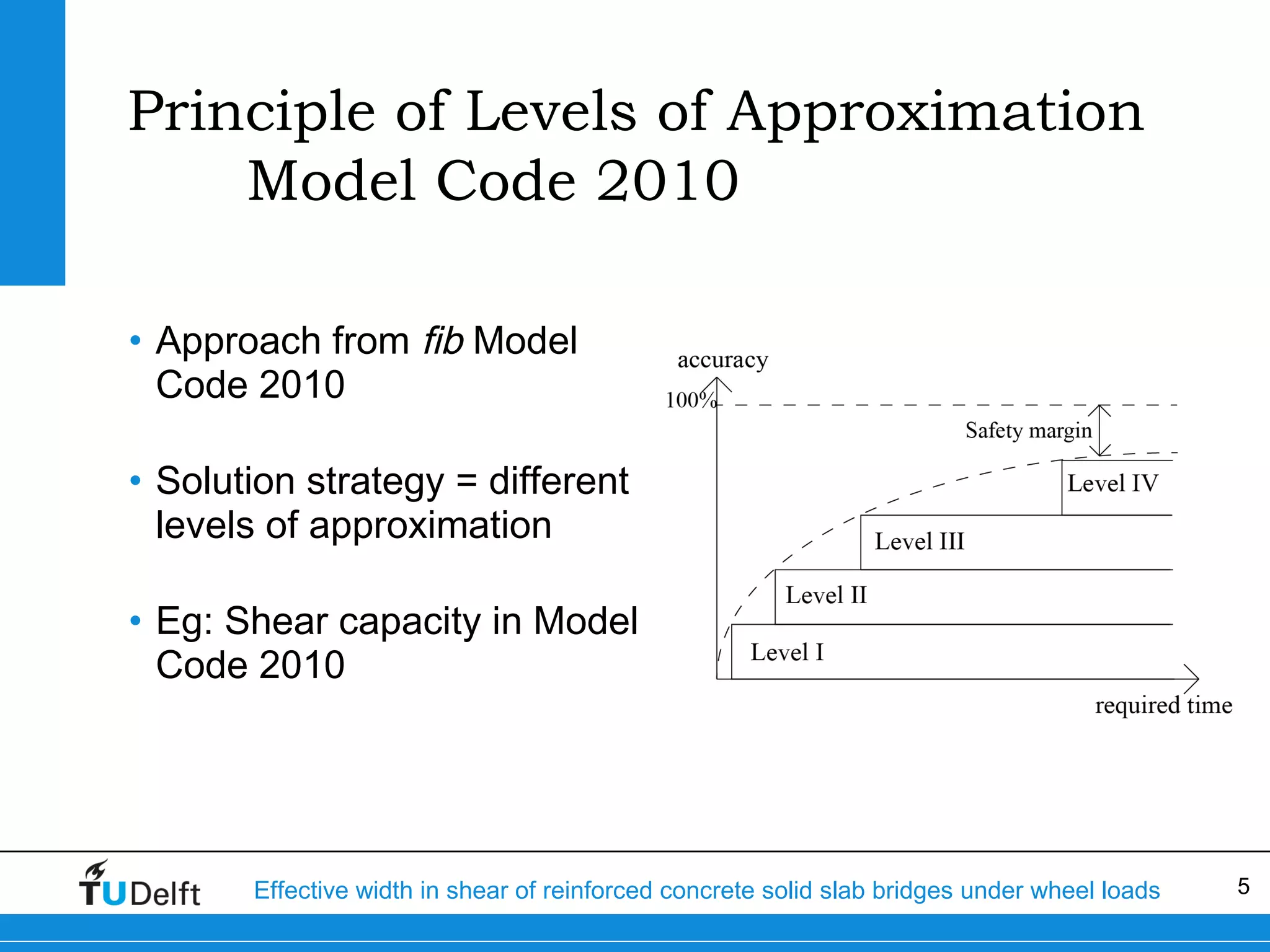
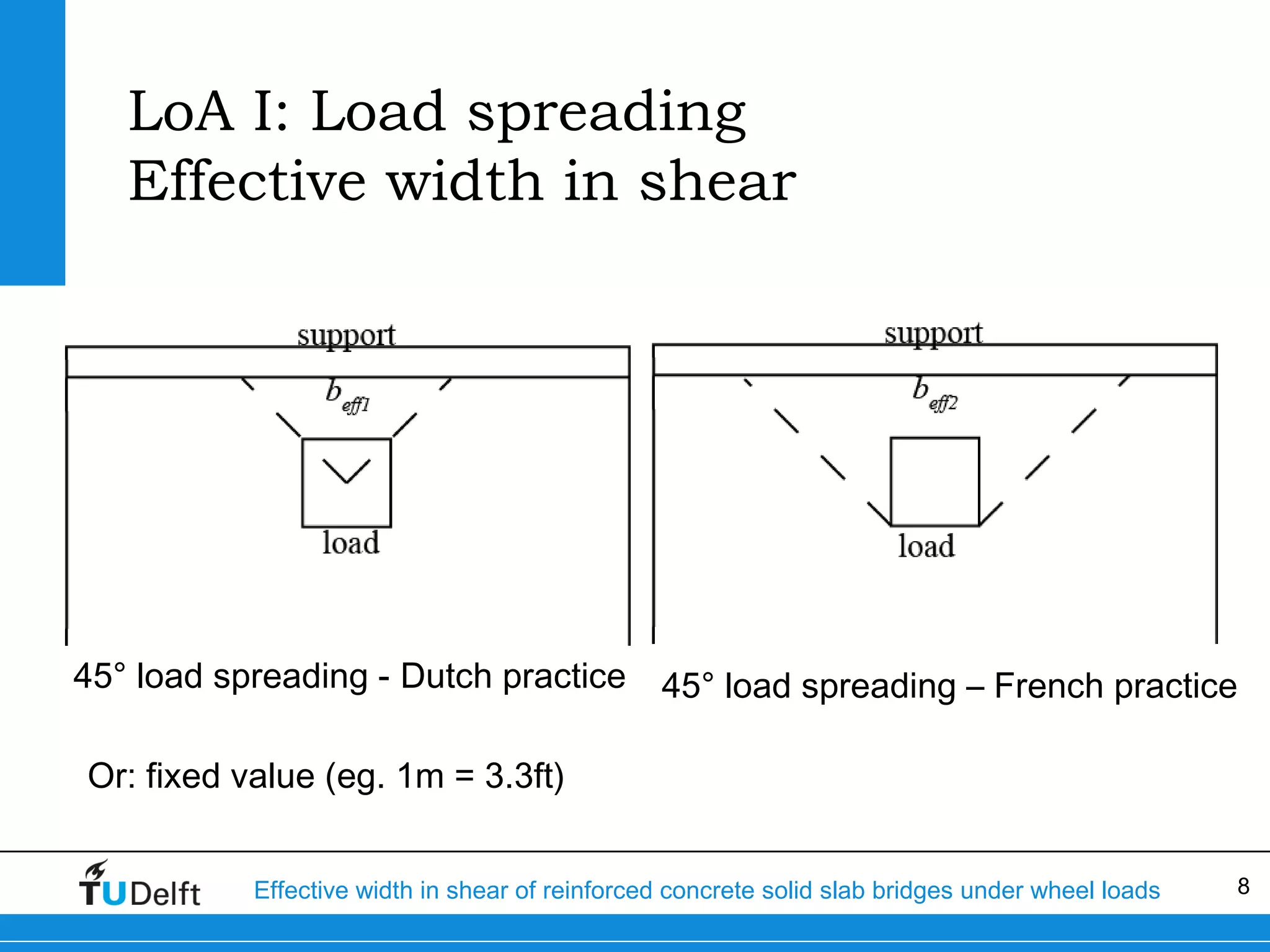
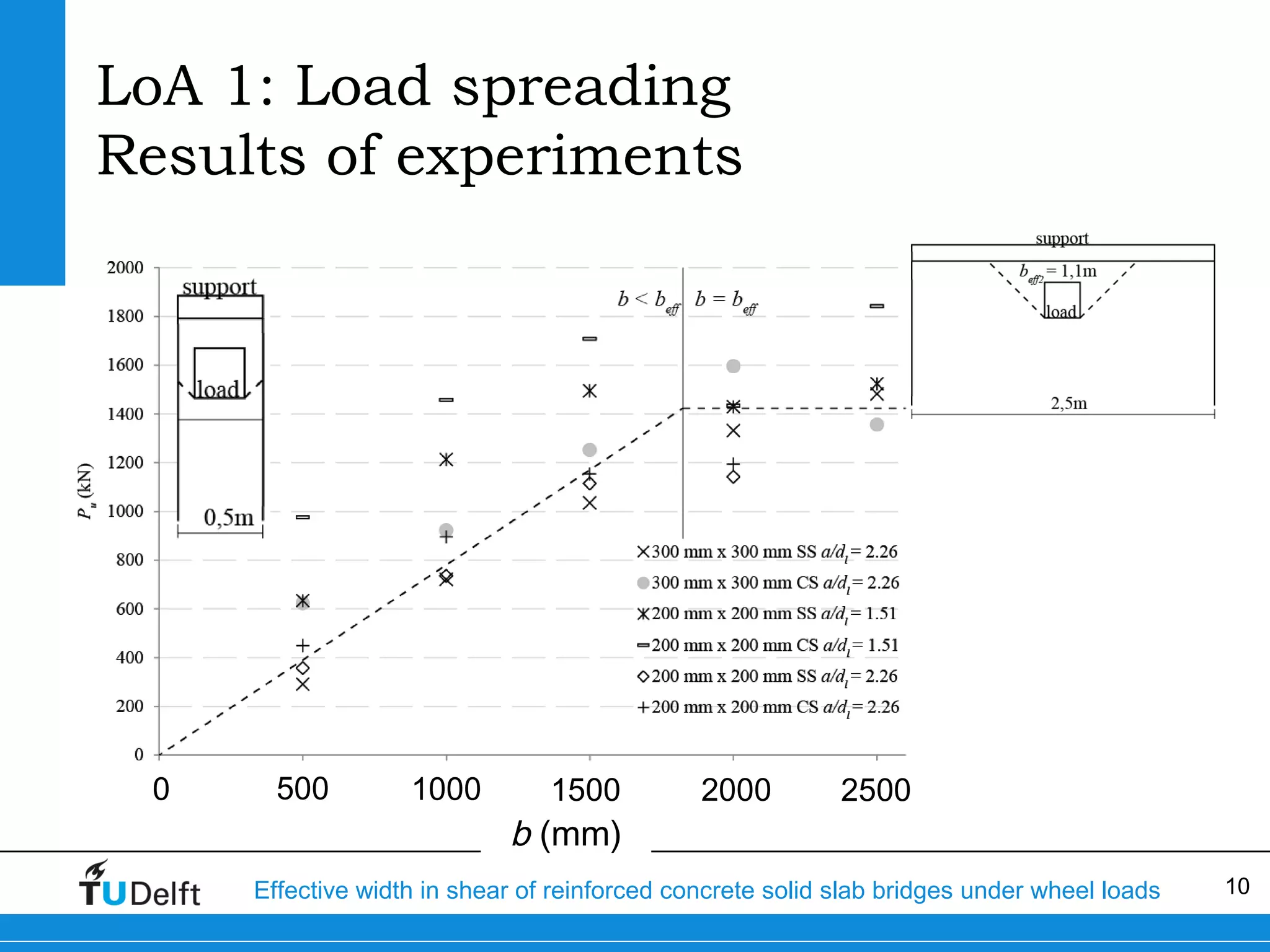
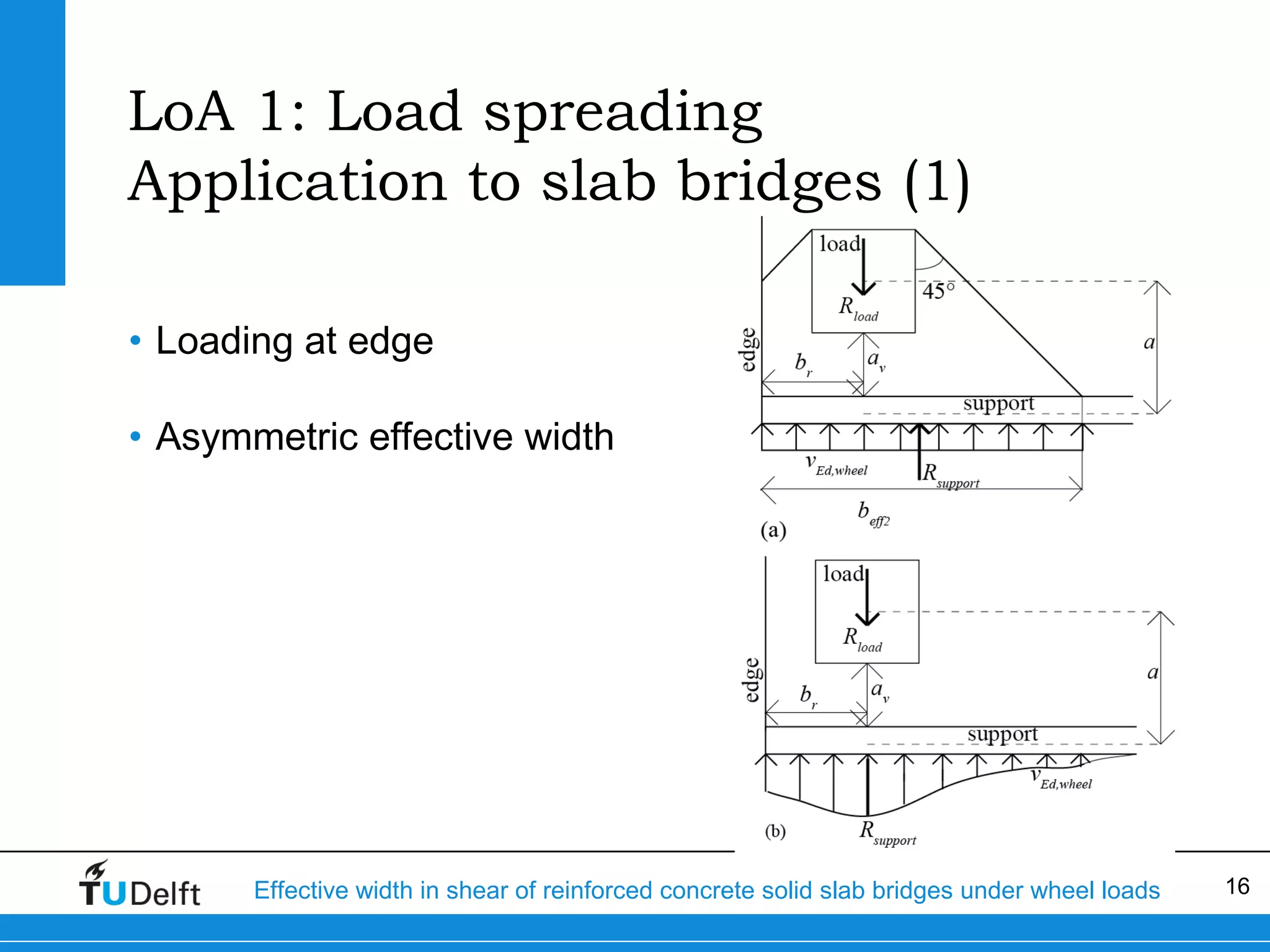
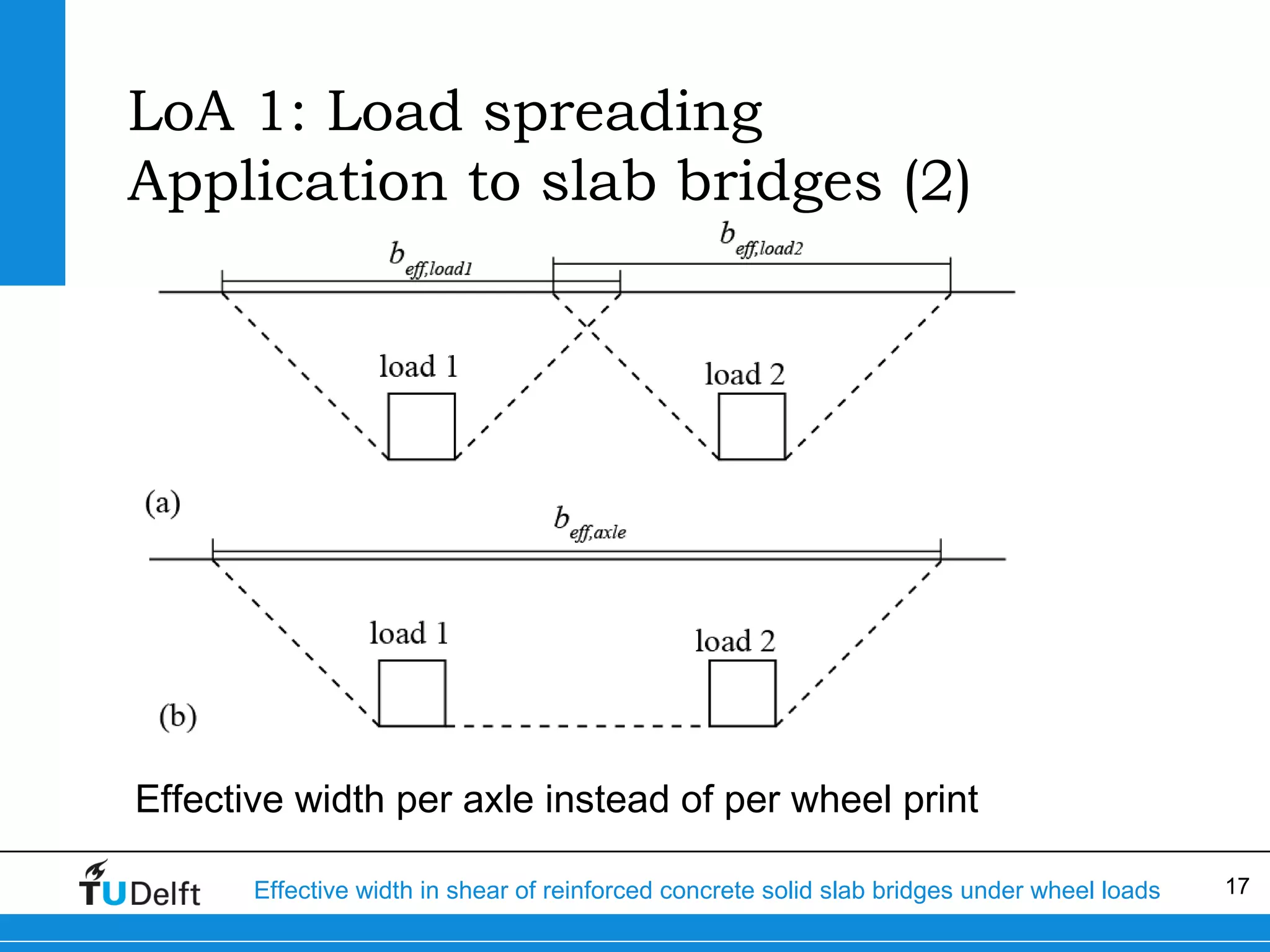
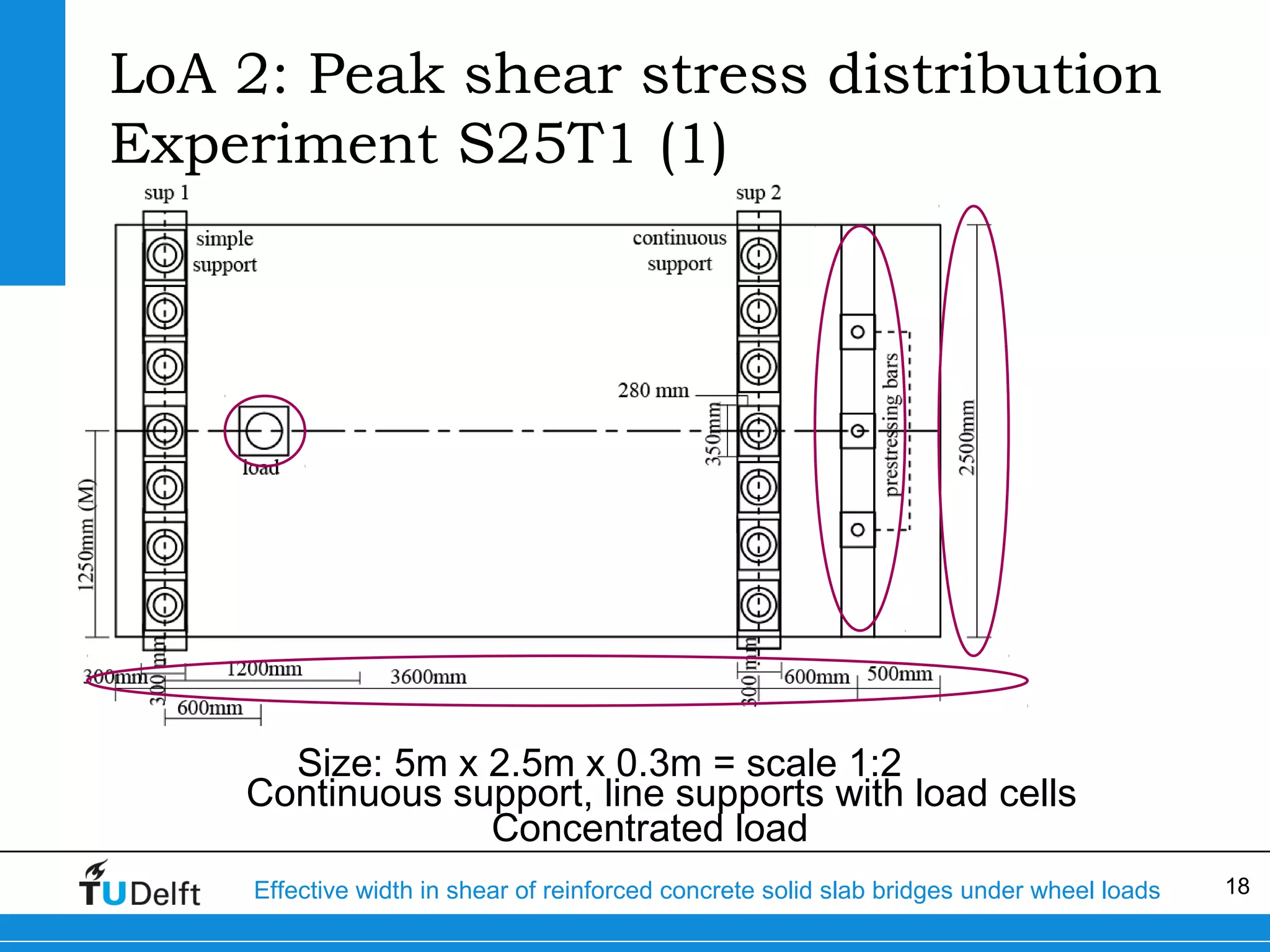
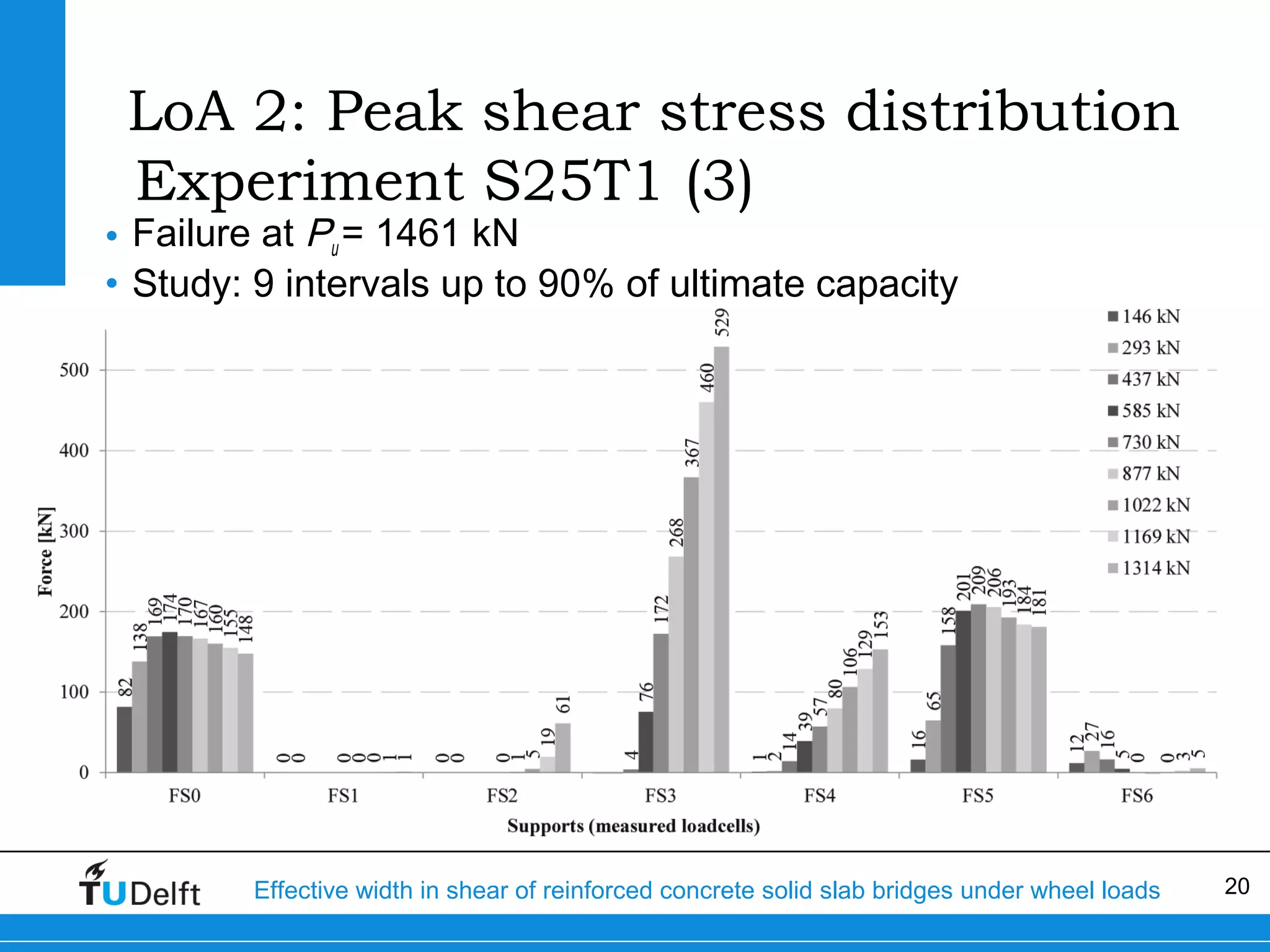
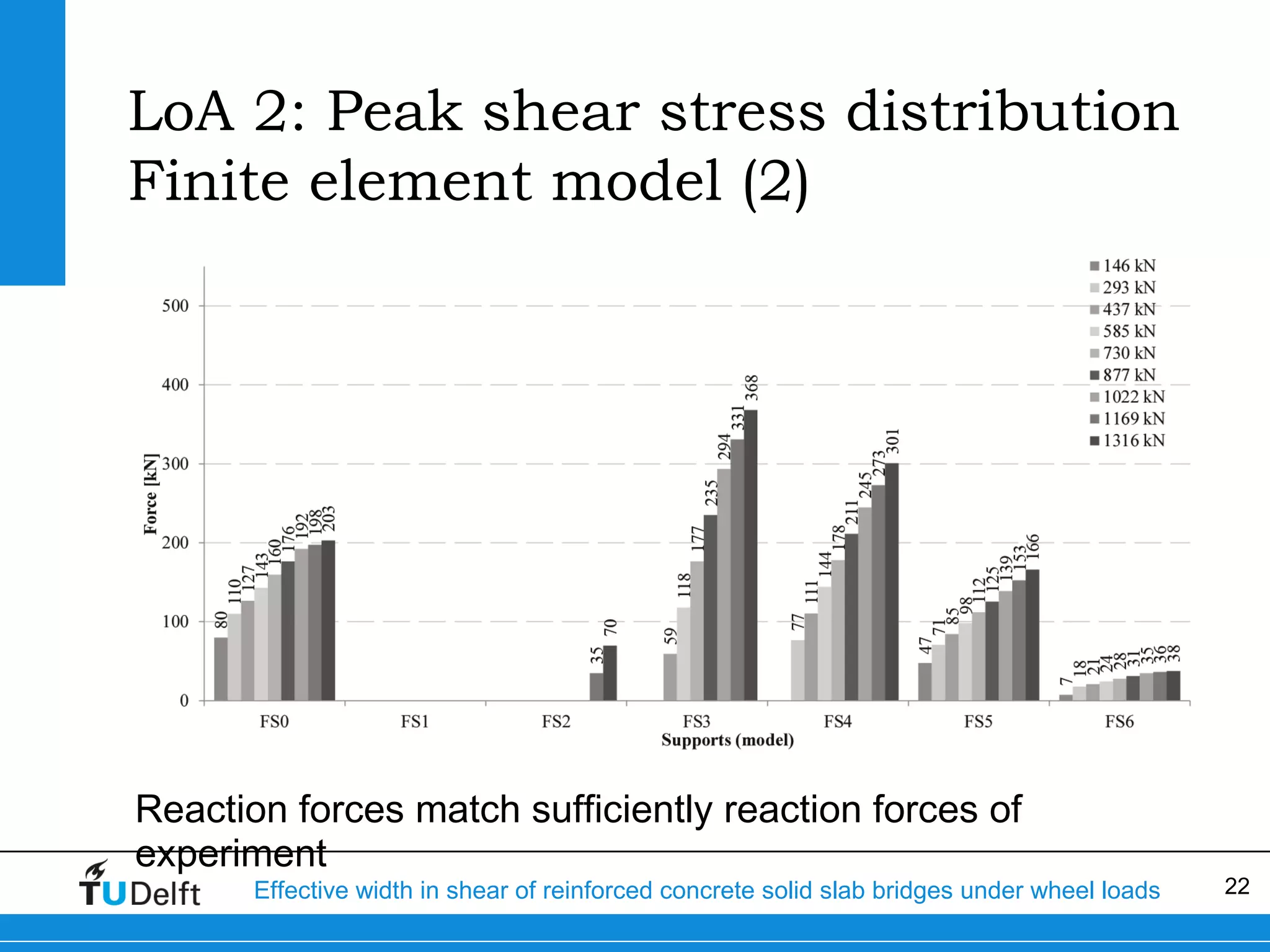
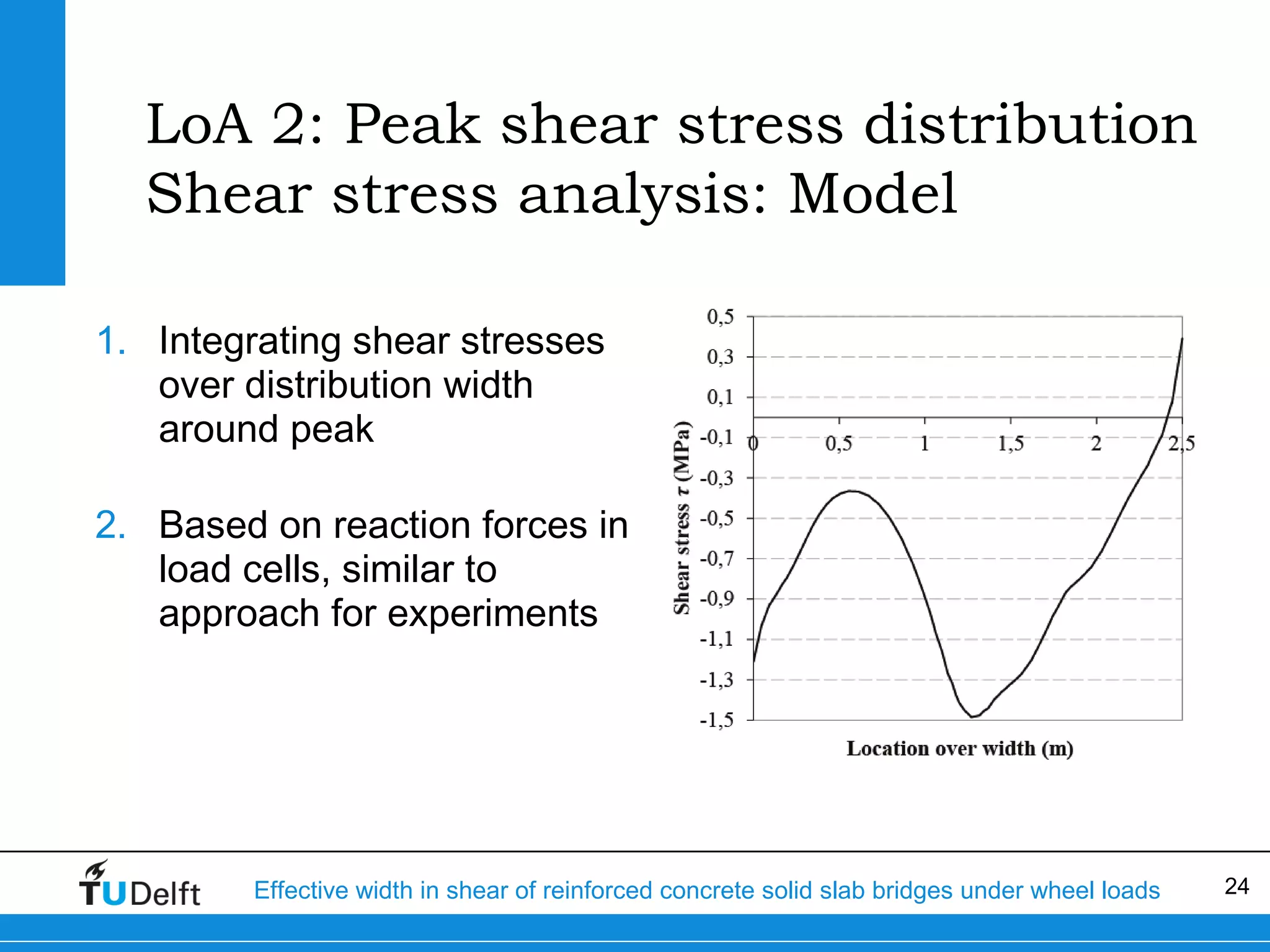
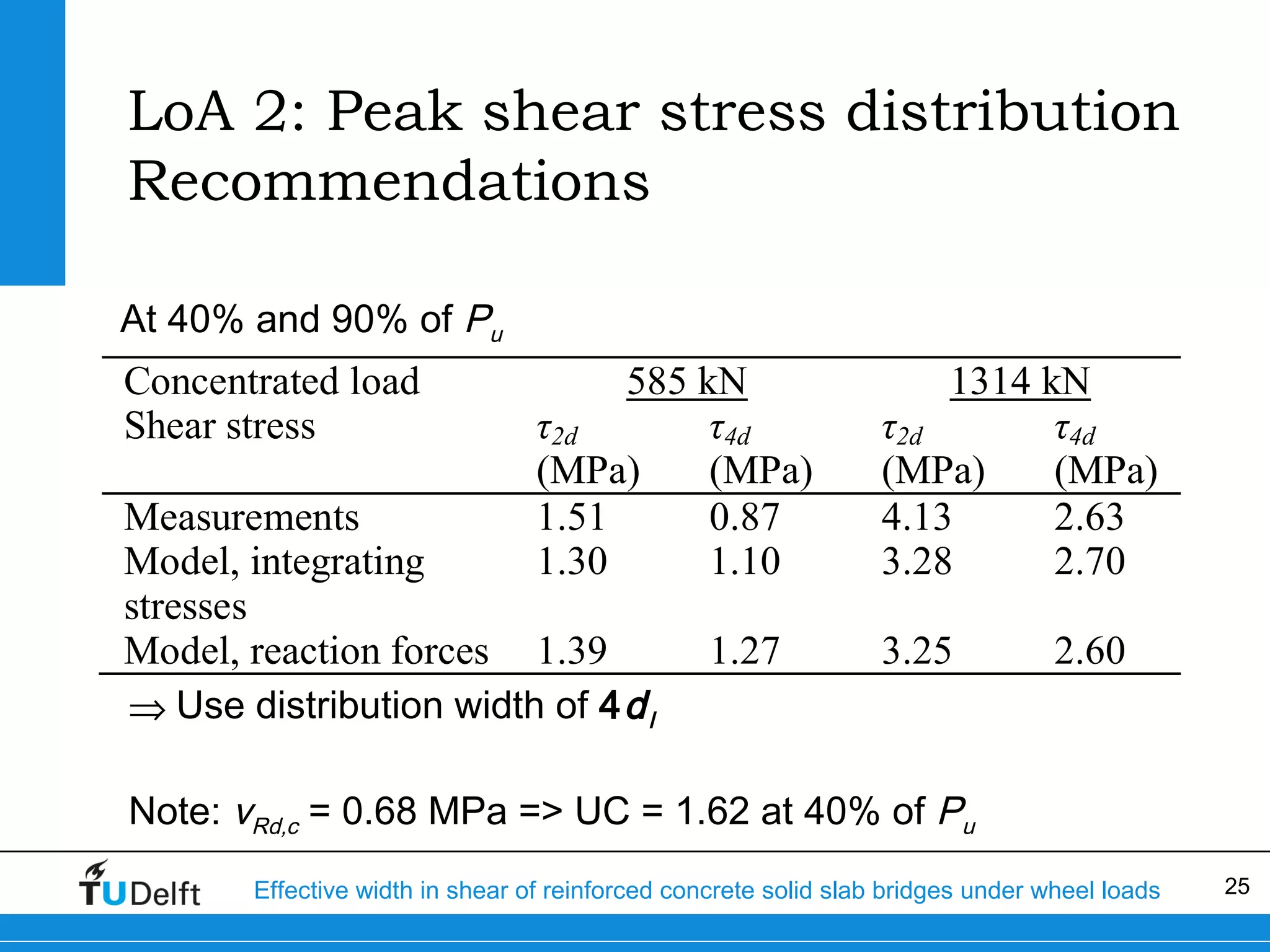
The document discusses the assessment of effective width in shear for reinforced concrete solid slab bridges under heavy wheel loads, focusing on methodologies from the fib model code 2010 and experimental findings. It compares two levels of assessment: a quick scan method and a finite element analysis, highlighting the conservative nature of the quick scan in assessing shear capacity. A case study illustrates that the quick scan method is more conservative compared to the finite element model results.
More Related Content
Similar to Effective Width in Shear of Reinforced Concrete Solid Slab Bridges under Wheel Loads
Effective Width in Shear of Reinforced Concrete Solid Slab Bridges under Wheel Loads
- 1. Effective width inshear Of reinforced concrete solid slab bridges under wheel loads 14-01-2014 Eva Lantsoght, Ane de Boer, Cor van der Veen, Joost Walraven Delft University of Technology Challenge the future
- 2. Overview • • • • • • • Introduction Principle of Levelsof Approximation Experiments LoA I: Load spreading LoA II: Shear stress distribution Case study Summary Effective width in shear of reinforced concrete solid slab bridges under wheel loads 2
- 3. Introduction Problem Statement Bridges from60s and 70s Increased live loads heavy and long truck (600 kN > perm. max = 50ton) The Hague in 1959 End of service life + larger loads Effective width in shear of reinforced concrete solid slab bridges under wheel loads 3
- 4. Introduction Highway network inthe Netherlands • NL: 60% of bridges built before 1976 • Assessment: shear critical in 600 slab bridges Highways in the Netherlands Effective width in shear of reinforced concrete solid slab bridges under wheel loads 4
- 5. Principle of Levelsof Approximation Model Code 2010 • Approach from fib Model Code 2010 • Solution strategy = different levels of approximation • Eg: Shear capacity in Model Code 2010 Effective width in shear of reinforced concrete solid slab bridges under wheel loads 5
- 6. Principle of Levelsof Approximation Shear assessment • Level I: Quick Scan sheet • Fast, simple and conservative spreadsheet • Unity check: loads/capacity • Level II: Finite Element Analysis • Shear stress distribution over support • Peak shear stress: distribute over which width? Effective width in shear of reinforced concrete solid slab bridges under wheel loads 6
- 7. Experiments Size: 5m x2.5m (variable) x 0.3m = scale 1:2 16ft x 8ft (variable) x 1ft Continuous support, Line supports Concentrated load: vary a/d and position along width Effective width in shear of reinforced concrete solid slab bridges under wheel loads 7
- 8. LoA I: Loadspreading Effective width in shear 45° load spreading - Dutch practice 45° load spreading – French practice Or: fixed value (eg. 1m = 3.3ft) Effective width in shear of reinforced concrete solid slab bridges under wheel loads 8
- 9. LoA 1: Loadspreading Results of experiments BS = 0.5m = 1.6 ft wide BX = 2.0m = 6.6ft wide Effective width in shear of reinforced concrete solid slab bridges under wheel loads 9
- 10. LoA 1: Loadspreading Results of experiments 0 500 1000 1500 b (mm) 2000 2500 Effective width in shear of reinforced concrete solid slab bridges under wheel loads 10
- 11. LoA 1: Loadspreading Statistical analysis • Calculated from series vs. 45° load spreading • Comparison between database (literature) + experiments and methods • French load spreading method underestimates less • Lower COV for French load spreading method • Database: 63% vs 42% • Delft experiments: 26% vs 22% Effective width in shear of reinforced concrete solid slab bridges under wheel loads 11
- 12. LoA 1: Loadspreading Finite element results (1) Models of 1.5m = 4.9ft wide a = center-to-center distance between load and support Effective width from shear stress distribution over support Effective width in shear of reinforced concrete solid slab bridges under wheel loads 12
- 13. LoA 1: Loadspreading Finite element results (2) Models of 2.5m = 8.2ft wide a = center-to-center distance between load and support Effective width from shear stress distribution over support Effective width in shear of reinforced concrete solid slab bridges under wheel loads 13
- 14. LoA 1: Loadspreading Finite element results (3) Models of 3.5m = 11.5ft wide a = center-to-center distance between load and support Effective width from shear stress distribution over support Effective width in shear of reinforced concrete solid slab bridges under wheel loads 14
- 15. LoA 1: Loadspreading Finite element results (4) • French load spreading method gives safe estimate of beff • NLFEA: beff depends slightly on slab width • NLFEA: influence of a/d less than in French method • French method sufficient for LoA 1 Effective width in shear of reinforced concrete solid slab bridges under wheel loads 15
- 16. LoA 1: Loadspreading Application to slab bridges (1) • Loading at edge • Asymmetric effective width Effective width in shear of reinforced concrete solid slab bridges under wheel loads 16
- 17. LoA 1: Loadspreading Application to slab bridges (2) Effective width per axle instead of per wheel print Effective width in shear of reinforced concrete solid slab bridges under wheel loads 17
- 18. LoA 2: Peakshear stress distribution Experiment S25T1 (1) Size: 5m x 2.5m x 0.3m = scale 1:2 Continuous support, line supports with load cells Concentrated load Effective width in shear of reinforced concrete solid slab bridges under wheel loads 18
- 19. LoA 2: Peakshear stress distribution Experiment S25T1 (2) Effective width in shear of reinforced concrete solid slab bridges under wheel loads 19
- 20. LoA 2: Peakshear stress distribution Experiment S25T1 (3) • Failure at Pu = 1461 kN • Study: 9 intervals up to 90% of ultimate capacity Effective width in shear of reinforced concrete solid slab bridges under wheel loads 20
- 21. LoA 2: Peakshear stress distribution Finite element model • TNO Diana • Slab: shell elements • Supports: solid elements • Felt: interface elements • 40% orthotropy assumed • Phased activation of supports Effective width in shear of reinforced concrete solid slab bridges under wheel loads 21
- 22. LoA 2: Peakshear stress distribution Finite element model (2) Reaction forces match sufficiently reaction forces of experiment Effective width in shear of reinforced concrete solid slab bridges under wheel loads 22
- 23. LoA 2: Peakshear stress distribution Shear stress analysis: Experiment • Assume force distributed constantly per load cell • Example: P = 1314 kN • Total force over 2dl 86 mm Ftot ,2 d = FS 3 + ( FS 2 + FS 4 ) = 580 kN 358 mm • Resulting shear stress τ 2d = Ftot ,2 d 2d l 2 = 580 kN 2 ( 265 mm ) 2 = 4.13 MPa Effective width in shear of reinforced concrete solid slab bridges under wheel loads 23
- 24. LoA 2: Peakshear stress distribution Shear stress analysis: Model 1. Integrating shear stresses over distribution width around peak 2. Based on reaction forces in load cells, similar to approach for experiments Effective width in shear of reinforced concrete solid slab bridges under wheel loads 24
- 25. LoA 2: Peakshear stress distribution Recommendations At 40% and 90% of Pu Concentrated load Shear stress 585 kN τ2d τ4d (MPa) (MPa) 1.51 0.87 1.30 1.10 Measurements Model, integrating stresses Model, reaction forces 1.39 ⇒ Use distribution width of 4 d l 1.27 1314 kN τ2d τ4d (MPa) (MPa) 4.13 2.63 3.28 2.70 3.25 2.60 Note: vRd,c = 0.68 MPa => UC = 1.62 at 40% of Pu Effective width in shear of reinforced concrete solid slab bridges under wheel loads 25
- 26. Case study Introduction • 4-spanbridge • • • • 1959 End spans = 10.1m (33.1ft) Mid spans = 14.4m (47.2ft) Width = 10m (32.8ft), 6m (19.7ft) carries traffic • QR24 reinforcement • fy = 240MPa = 35ksi • plain reinforcement • fck = 35MPa = 5000psi Effective width in shear of reinforced concrete solid slab bridges under wheel loads 26
- 27. Case Study Results • LoA1 • vEd = 0.68MPa (99psi) • vRd,c = 0.91MPa (132psi) ⇒UC = 0.74 • LoA 2: • VEd = 278kN/m (19kip/ft) • VRd,c = 438kN/m (30kip/ft) ⇒UC = 0.63 • LoA 1 more conservative than LoA 2 Effective width in shear of reinforced concrete solid slab bridges under wheel loads 27
- 28. Summary & Conclusions 1.Level I of Assessment: Quick Scan method: French load spreading method 2. Level II of Assessment: Finite Element Model: Distribute peak shear stress over 4dl 3. Case study: LoA 1 more conservative than LoA 2 Effective width in shear of reinforced concrete solid slab bridges under wheel loads 28
- 29. Contact: Eva Lantsoght E.O.L.Lantsoght@tudelft.nl +31(0)152787449 Effective widthin shear of reinforced concrete solid slab bridges under wheel loads 29