Uploaded byEva Lantsoght
Lekenpraatje
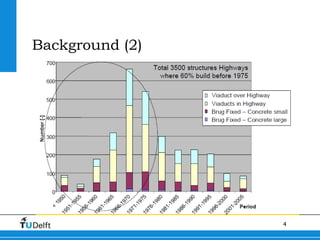
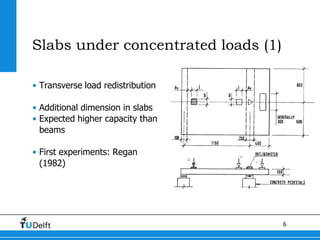
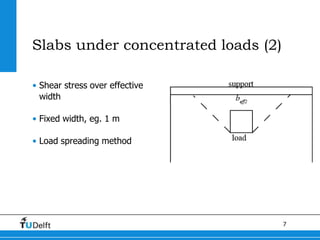
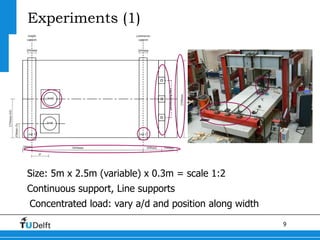
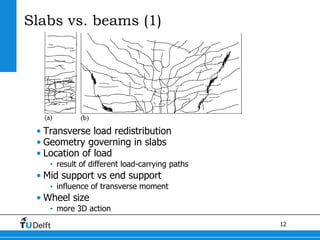
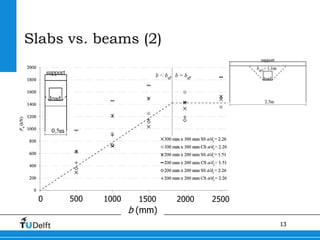
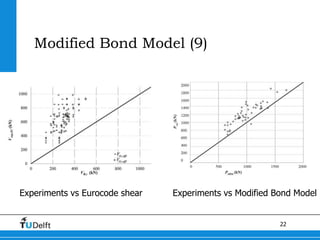
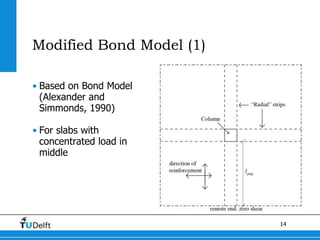
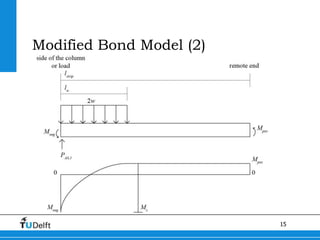
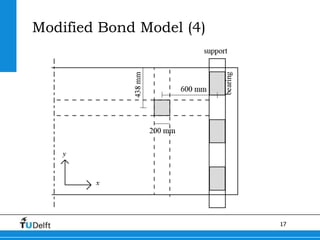
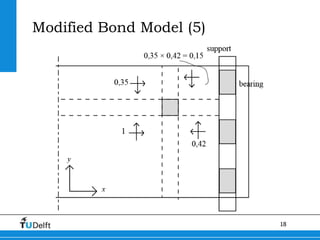
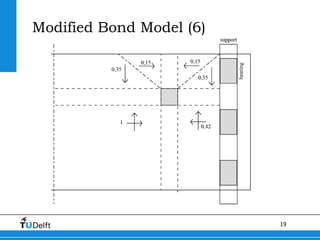
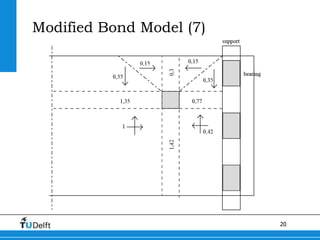
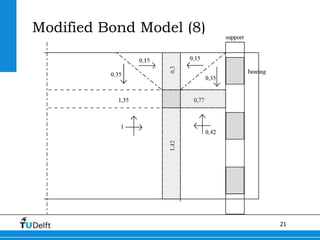
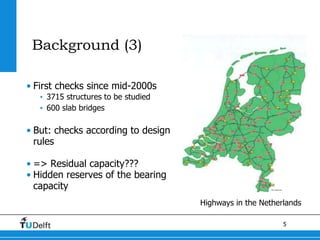
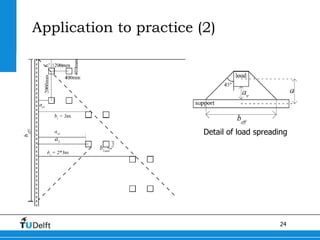
1) The document discusses shear capacity in reinforced concrete slabs under concentrated loads close to supports. Experiments were conducted on slab specimens to determine the effective width in shear. 2) A Modified Bond Model was developed to better model the behavior of slabs under concentrated loads near supports. This model accounts for the geometry governing load redistribution in slabs. 3) The Modified Bond Model was applied to evaluate the shear capacity of existing solid slab bridges in the Netherlands according to Eurocode recommendations and the modified approach. The modified approach generally resulted in an 18% reduction in shear loads and improved selection of bridge sections for assessment.
More Related Content
Lekenpraatje
- 1. Challenge the future Delft Universityof Technology Shear in Reinforced Concrete Slabs under Concentrated Loads close to Supports Eva Lantsoght
- 2. 2 Overview • Background • Slabsunder concentrated loads • Overview of experiments • Beams vs. slabs • Modified Bond Model • Application to practice • Conclusions
- 3. 3 Background (1) Bridges from60s and 70s The Hague in 1959 Increased live loads common heavy and long truck (600 kN) End of service life + larger loads
- 4.
- 5. 5 Background (3) • Firstchecks since mid-2000s • 3715 structures to be studied • 600 slab bridges • But: checks according to design rules • => Residual capacity??? • Hidden reserves of the bearing capacity Highways in the Netherlands
- 6. 6 Slabs under concentratedloads (1) • Transverse load redistribution • Additional dimension in slabs • Expected higher capacity than beams • First experiments: Regan (1982)
- 7. 7 Slabs under concentratedloads (2) • Shear stress over effective width • Fixed width, eg. 1 m • Load spreading method
- 8. 8 Goals • Assess shearcapacity of slabs under concentrated loads • Determine effective width in shear
- 9. 9 Experiments (1) Size: 5mx 2.5m (variable) x 0.3m = scale 1:2 Continuous support, Line supports Concentrated load: vary a/d and position along width
- 10. 10 Experiments (2) • 2ndseries experimental work: • Slabs under combined loading • Line load • Preloading • 50% of strength from slab strips • Concentrated load • loading until failure • Conclusions from 1st series valid when combining loads? • Total: 26 experiments, 8 slabs
- 11.
- 12. 12 Slabs vs. beams(1) • Transverse load redistribution • Geometry governing in slabs • Location of load • result of different load-carrying paths • Mid support vs end support • influence of transverse moment • Wheel size • more 3D action
- 13. 13 Slabs vs. beams(2) 5000 1000 1500 2000 2500 b (mm)
- 14. 14 Modified Bond Model(1) • Based on Bond Model (Alexander and Simmonds, 1990) • For slabs with concentrated load in middle
- 15.
- 16. 16 Modified Bond Model(3) • Adapted for slabs with concentrated load close to support • Geometry is governing as in experiments • Determine factor that reduces capacity of “radial” strip • Maximum load: based on sum capacity of 4 strips
- 17.
- 18.
- 19.
- 20.
- 21.
- 22. 22 Modified Bond Model(9) Experiments vs Eurocode shear Experiments vs Modified Bond Model
- 23. 23 Application to practice(1) • Evaluating existing solid slab bridges: • EN 1992-1-1:2005 • 25% reduction of contribution concentrated load close to support • β =av/2d • Combined: βnew =av/2,5d • Effective width: French method and minimum 4d
- 24. 24 Application to practice(2) Detail of load spreading
- 25. 25 Application to practice(3) • Checks at indicated sections • 9 existing Dutch solid slab bridges + MBE example
- 26. 26 Application to practice(4) • Shear stresses: influence of recommendations • QS-EC2: wheel loads at av = 2,5dl • QS-VBC: wheel loads at av = dl • QS-EC2 18% reduction in loads • Shear capacity: • QS-EC2: vRd,c ~ ρ, d • low reinforcement + deep section = small shear capacity • QS-VBC: τ1 ~ fck only • QS-EC2 improved selection ability
- 27. 27 Economics • Repair cost •Demolition cost • Recycling cost • New construction Environment • Impact of repair • Impact of replacement • CO2 emissions • Materials • Transport Social • Visual impact • Traffic delays • Employment Sustainability
- 28. 28 Summary & Conclusions •Slabs under concentrated loads behave differently in shear than beams • Beneficial effect of transverse load redistribution • Modified Bond Model improvement as compared to Eurocode • Application to practice: reduction in loads
- 29.