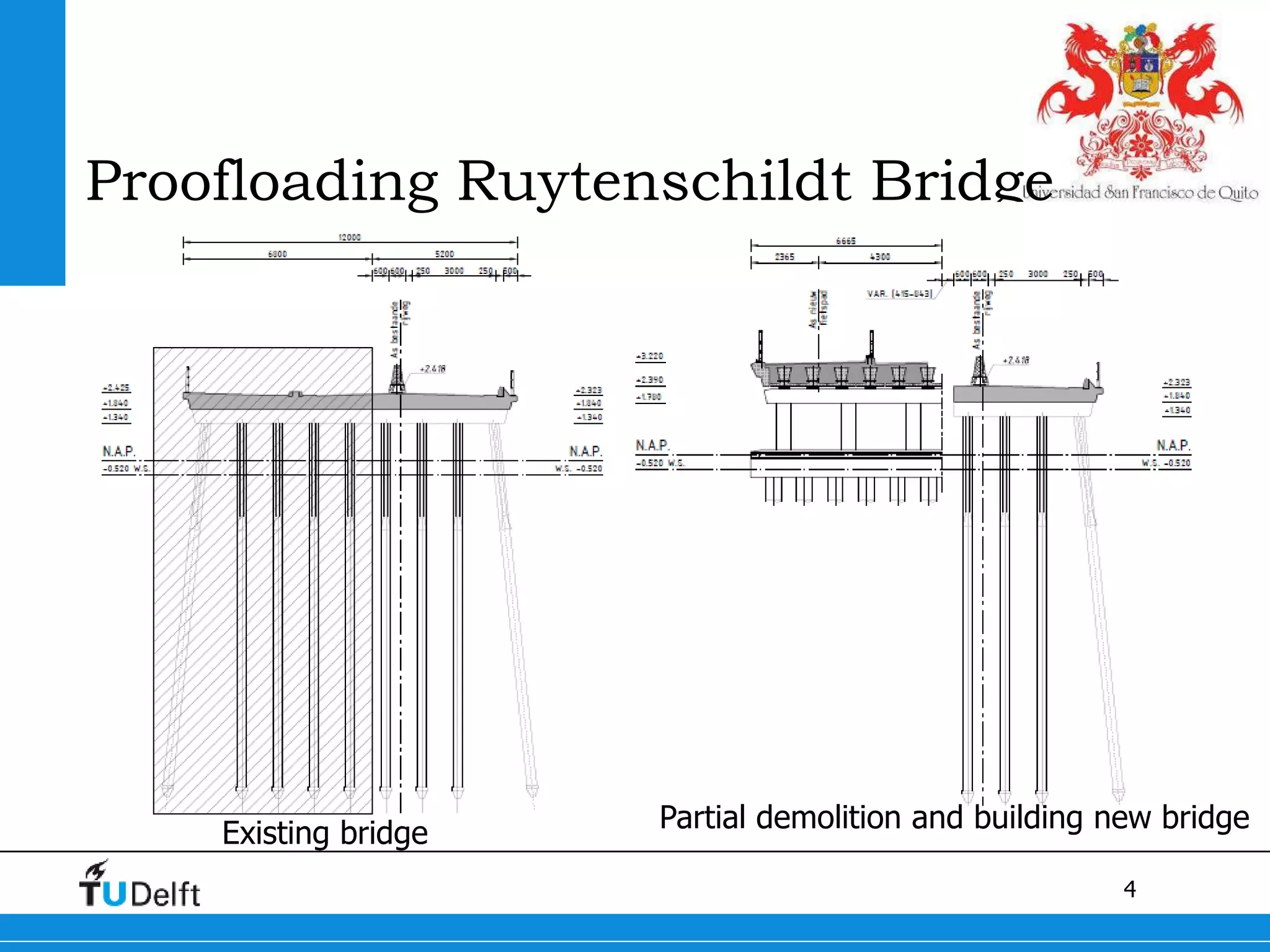
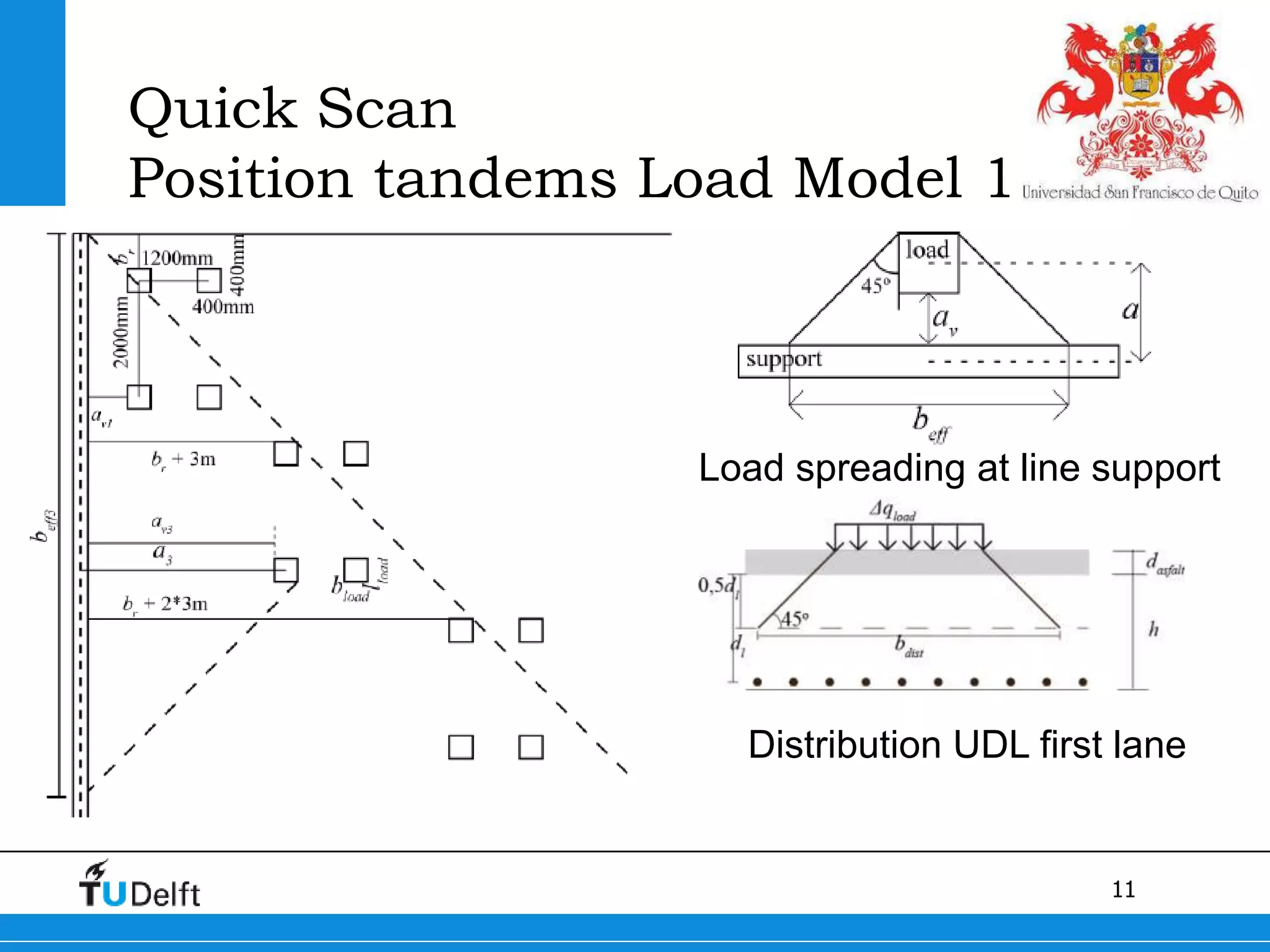
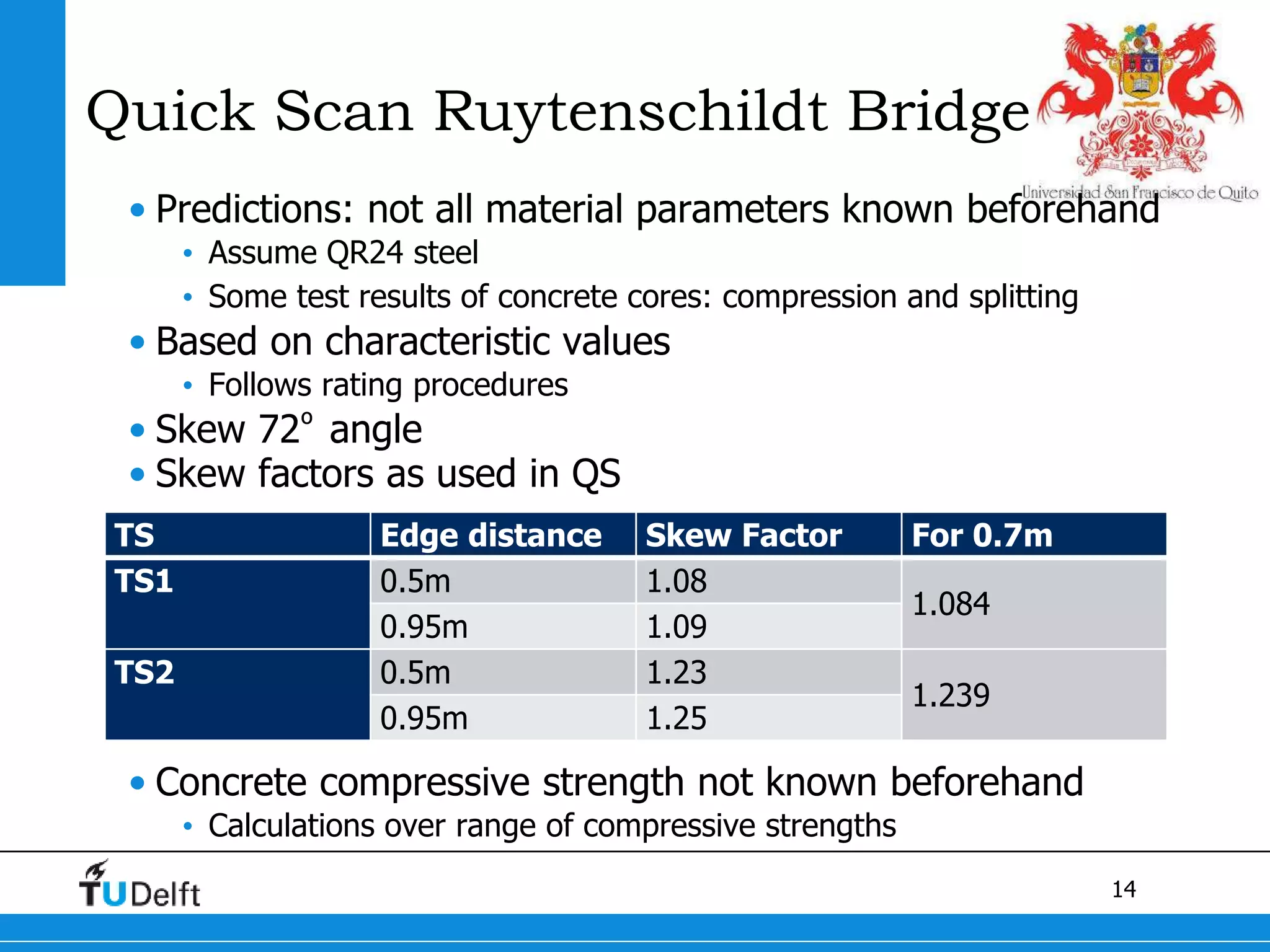
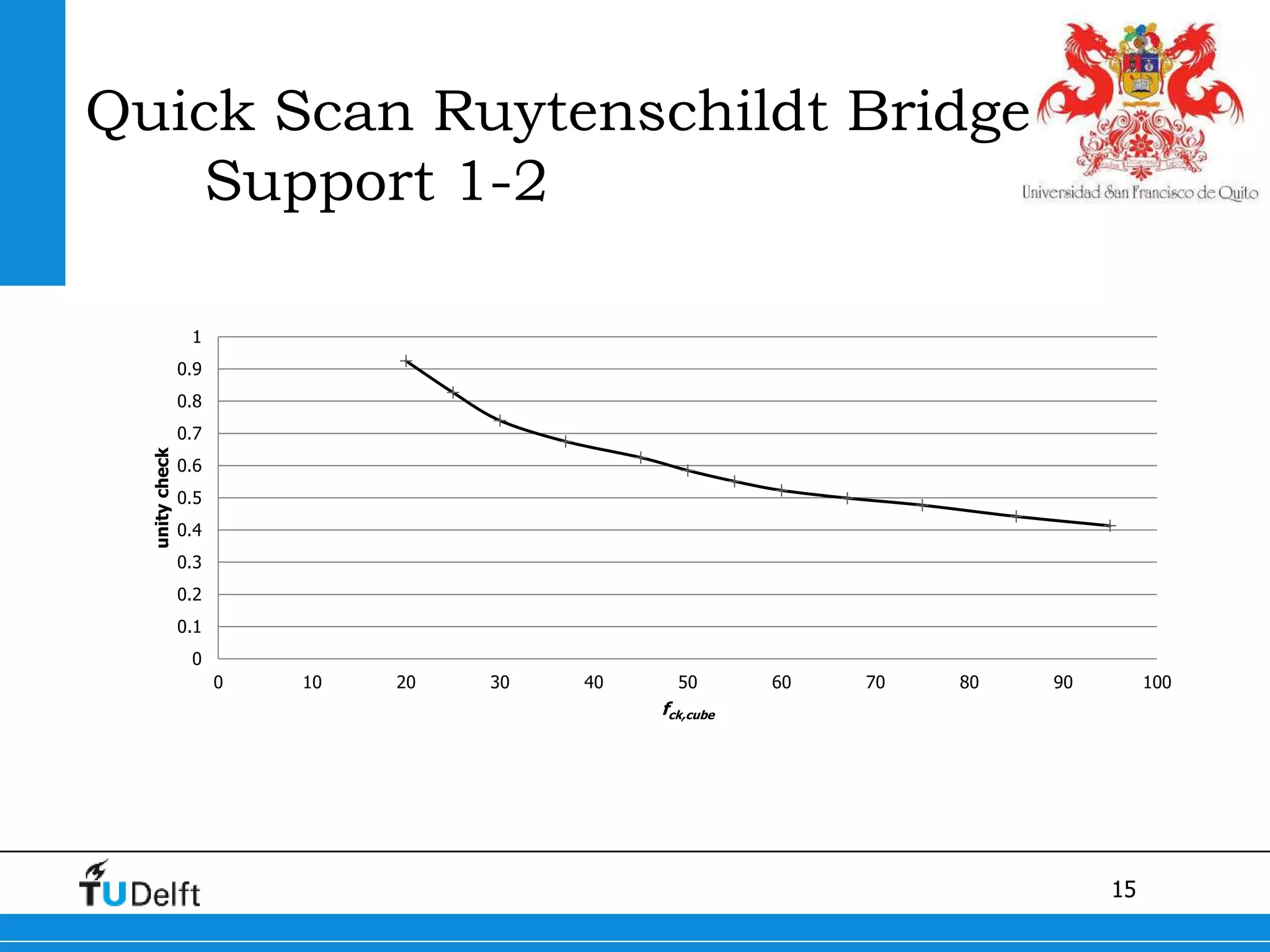
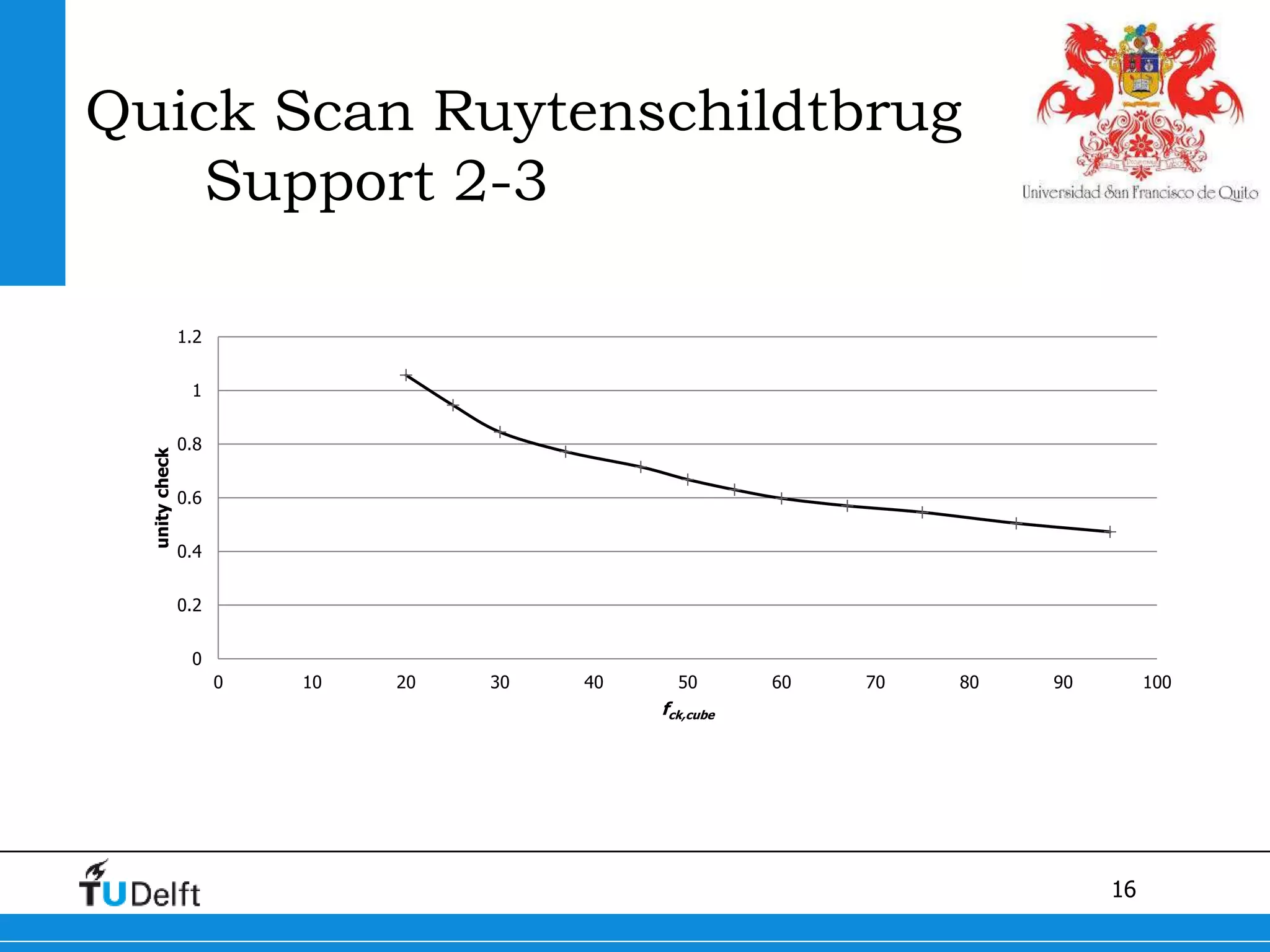
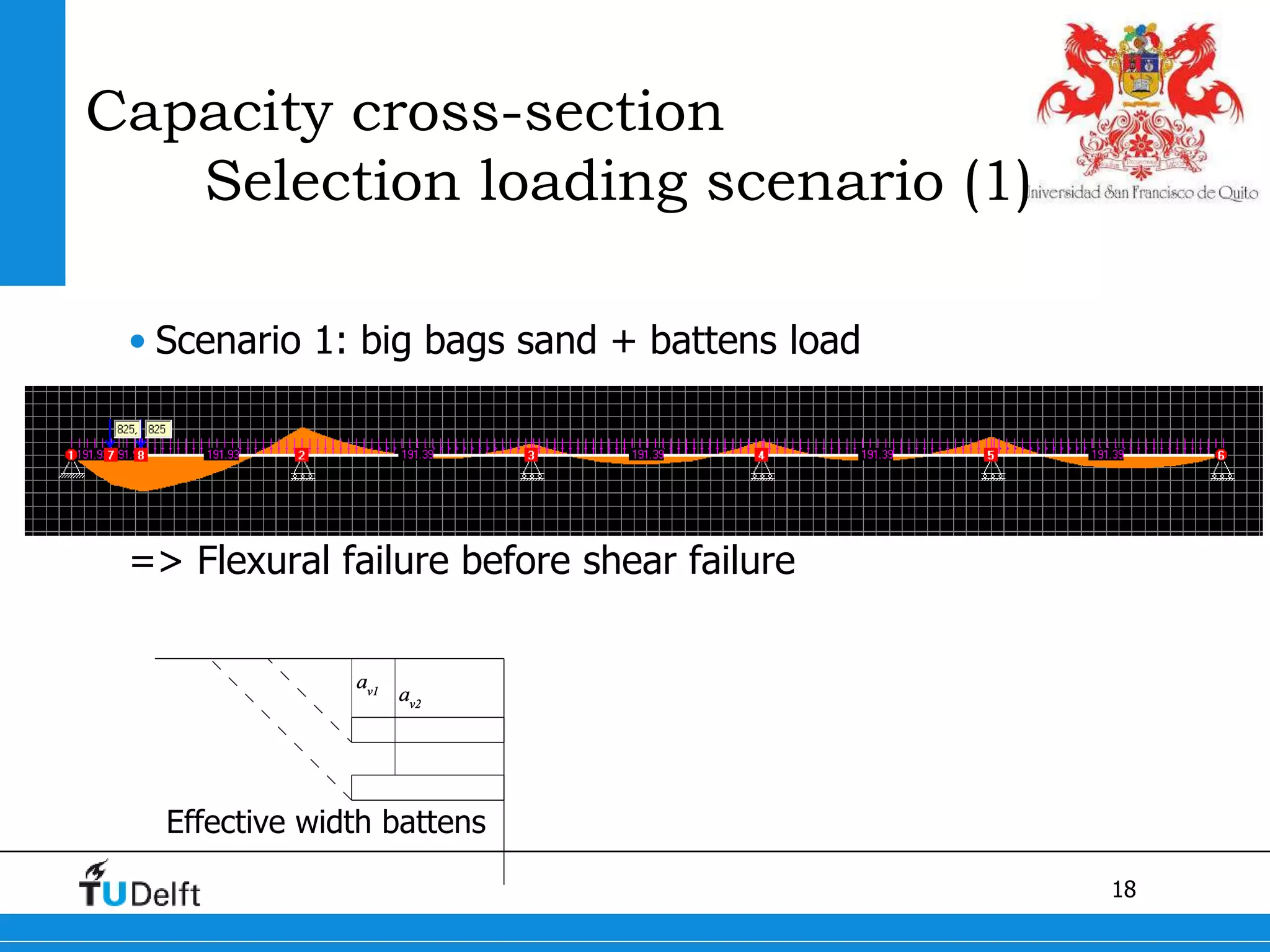
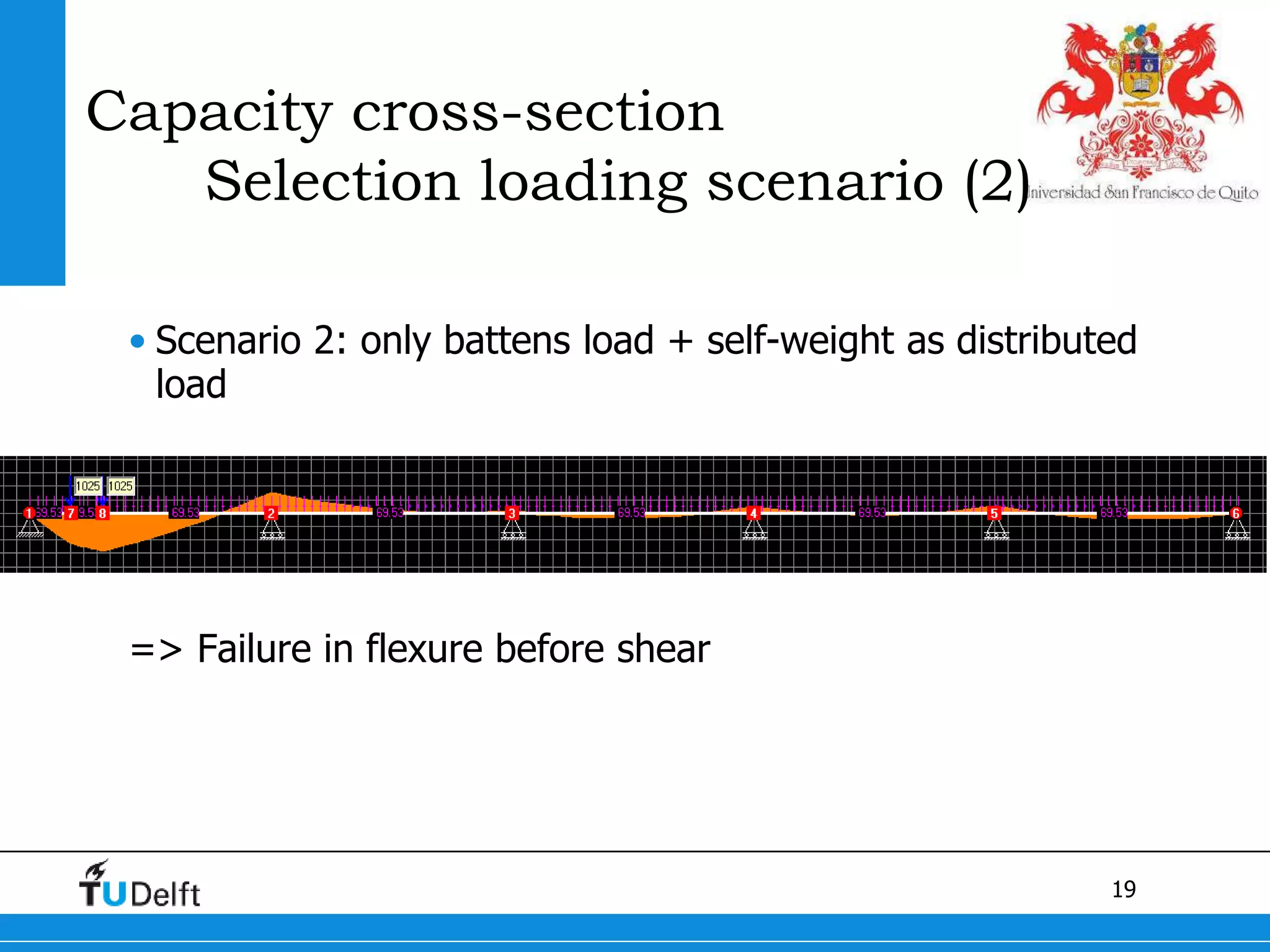
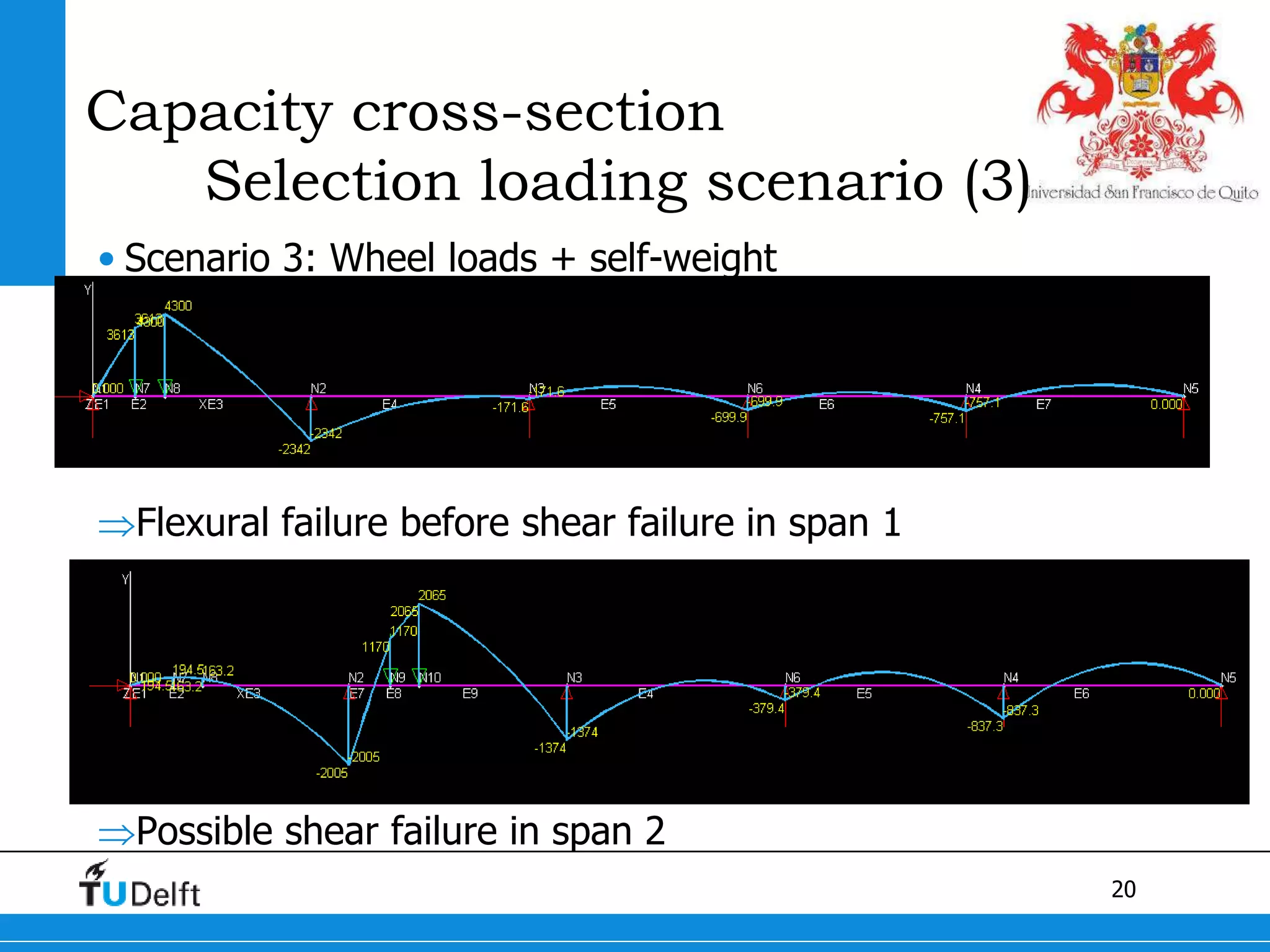
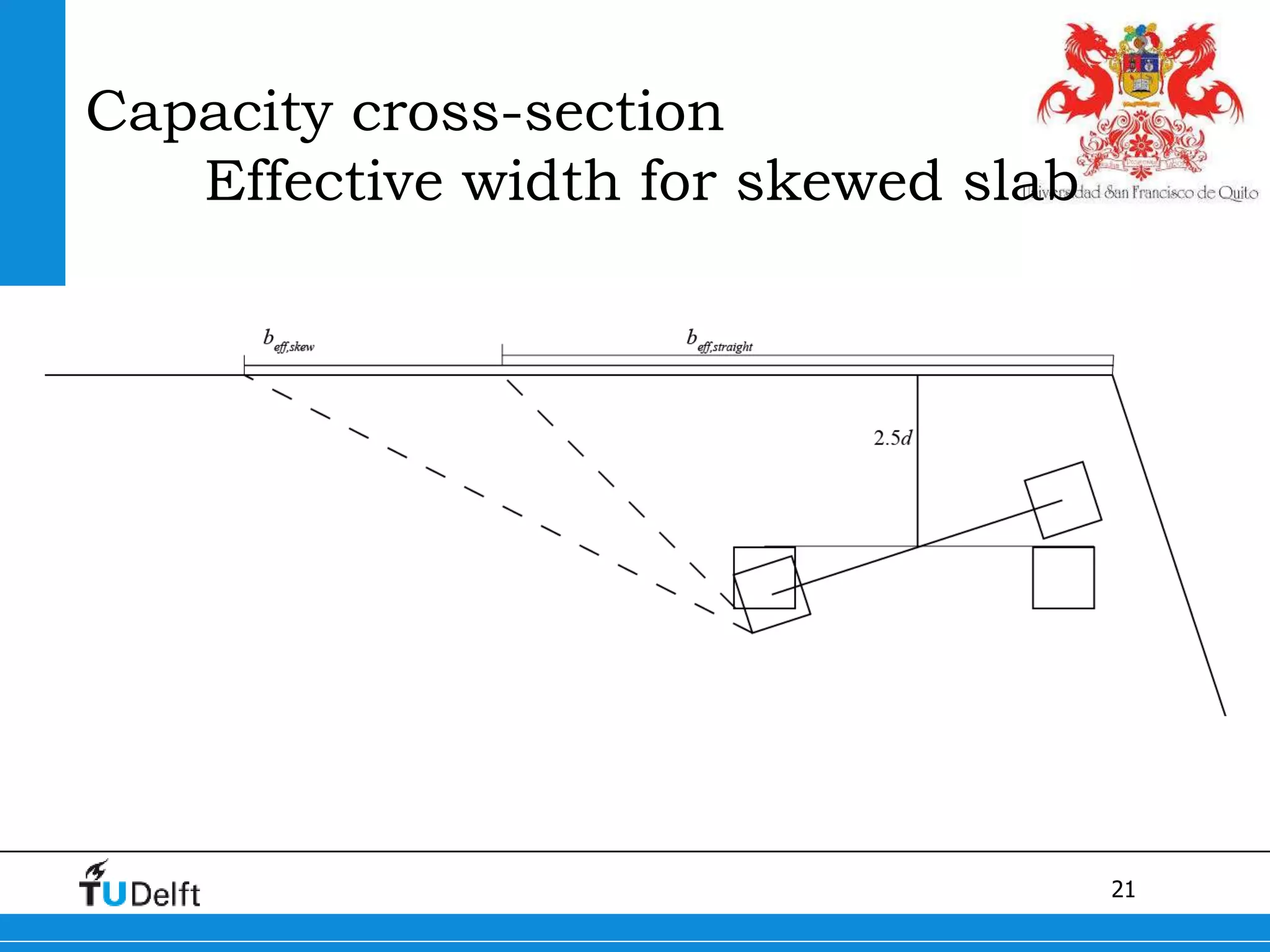
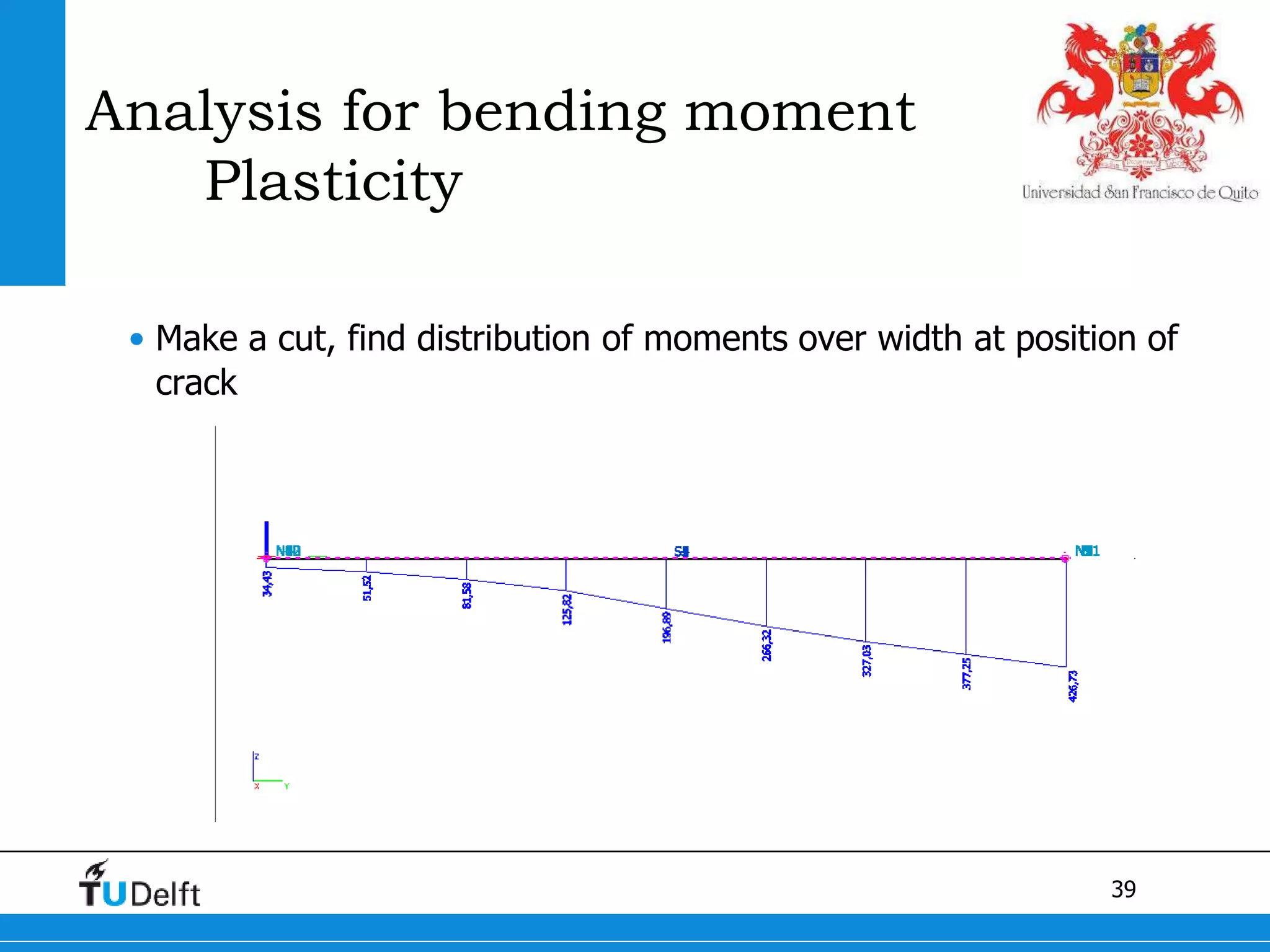
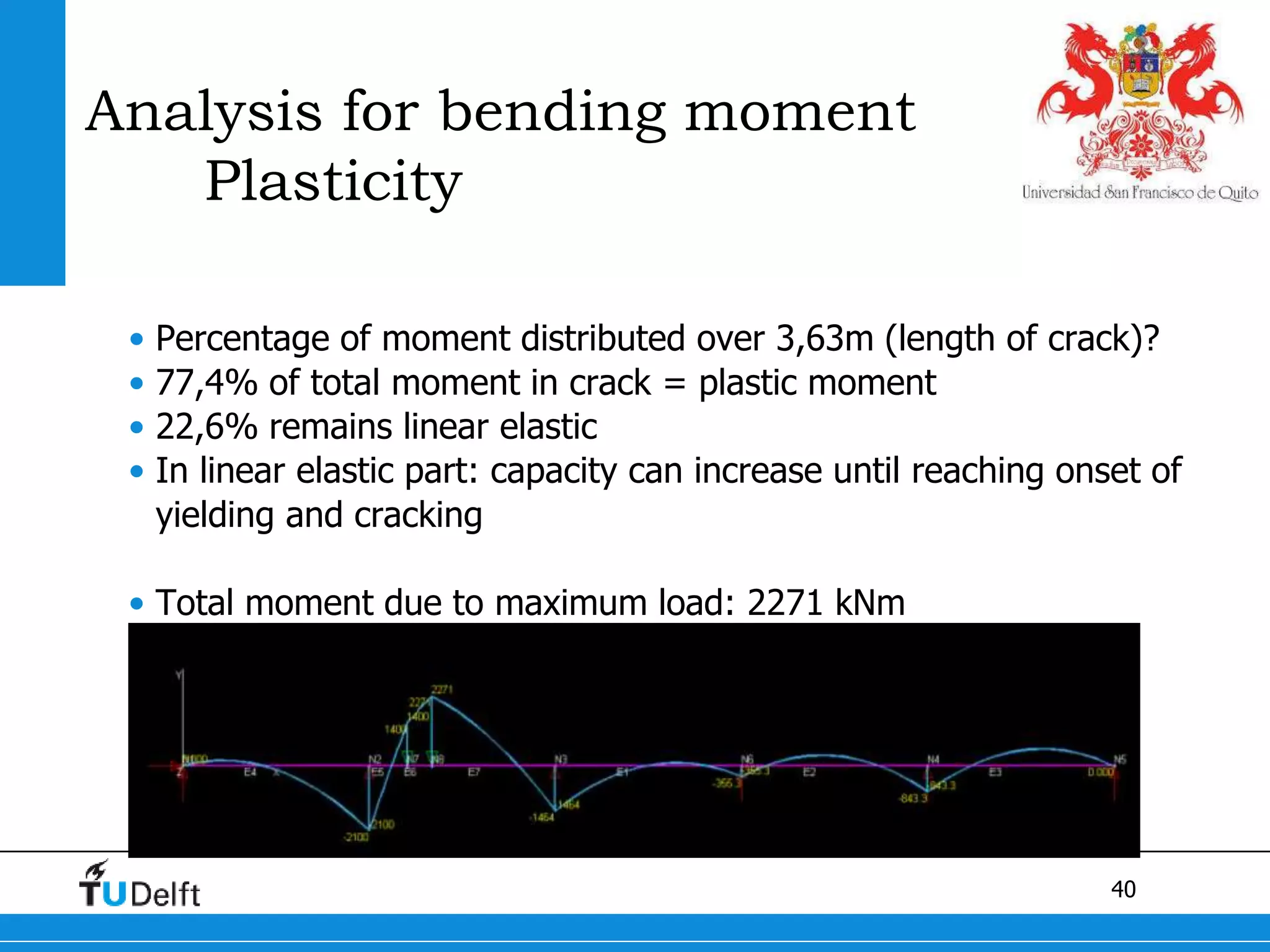
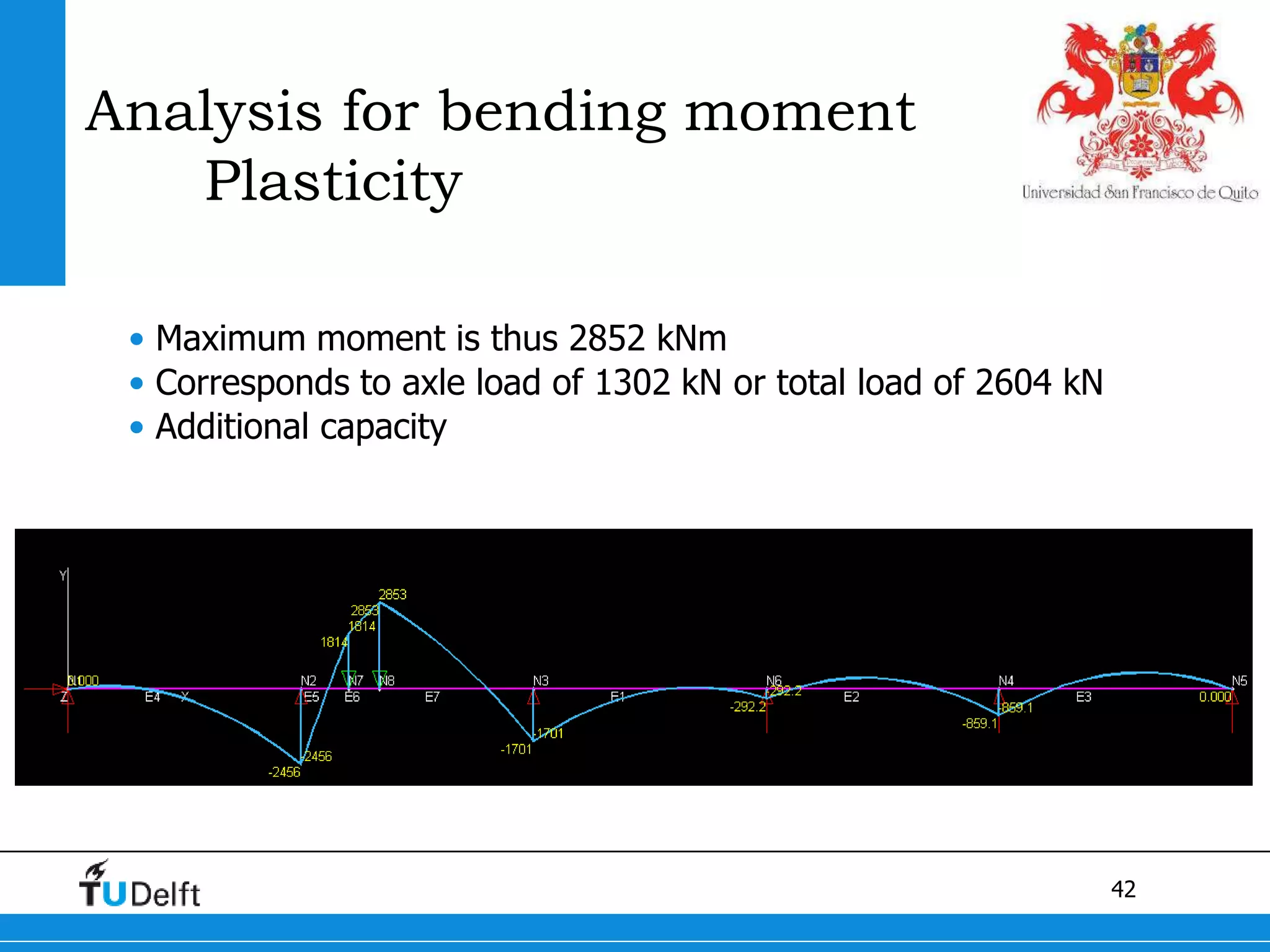
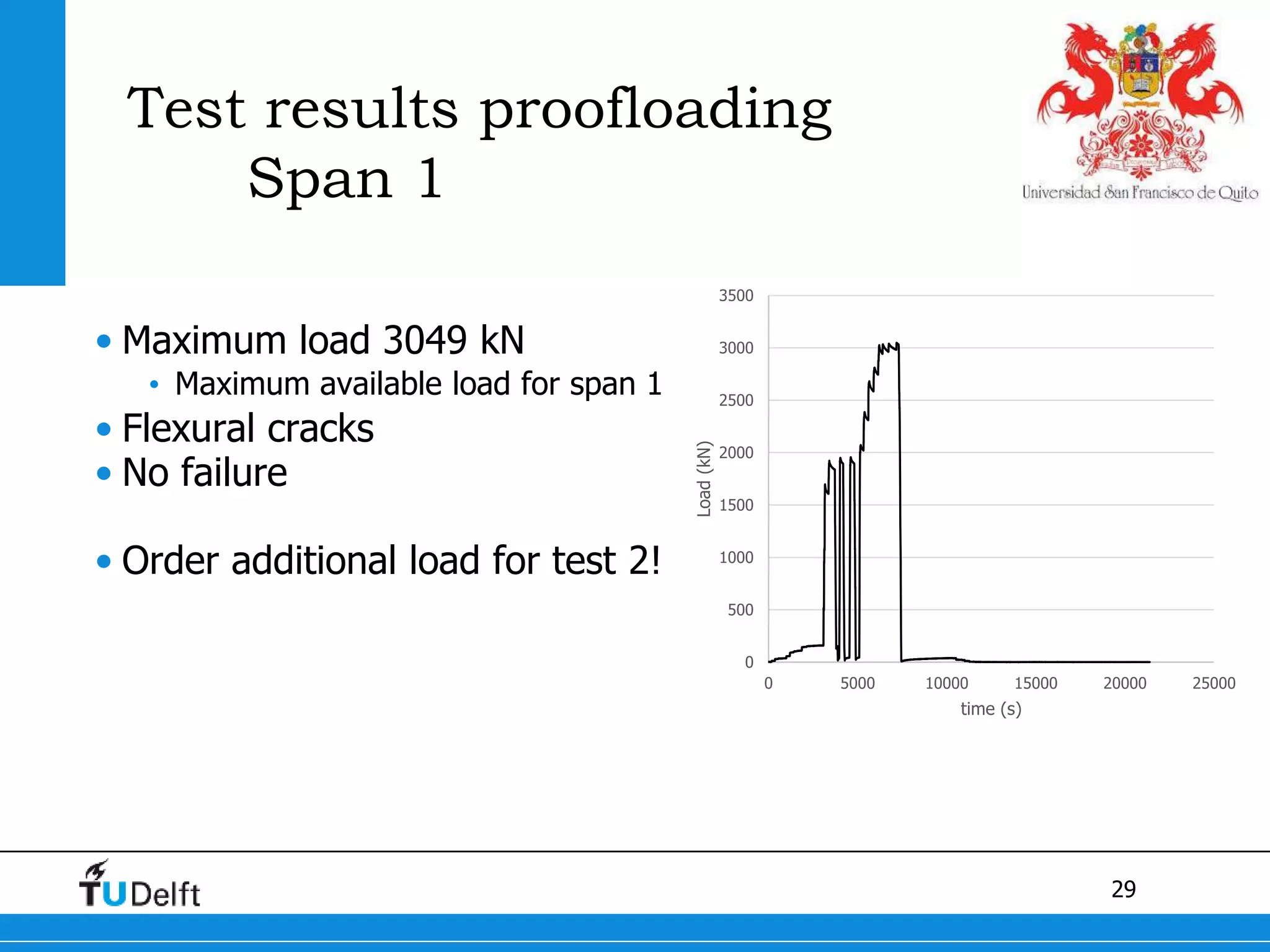
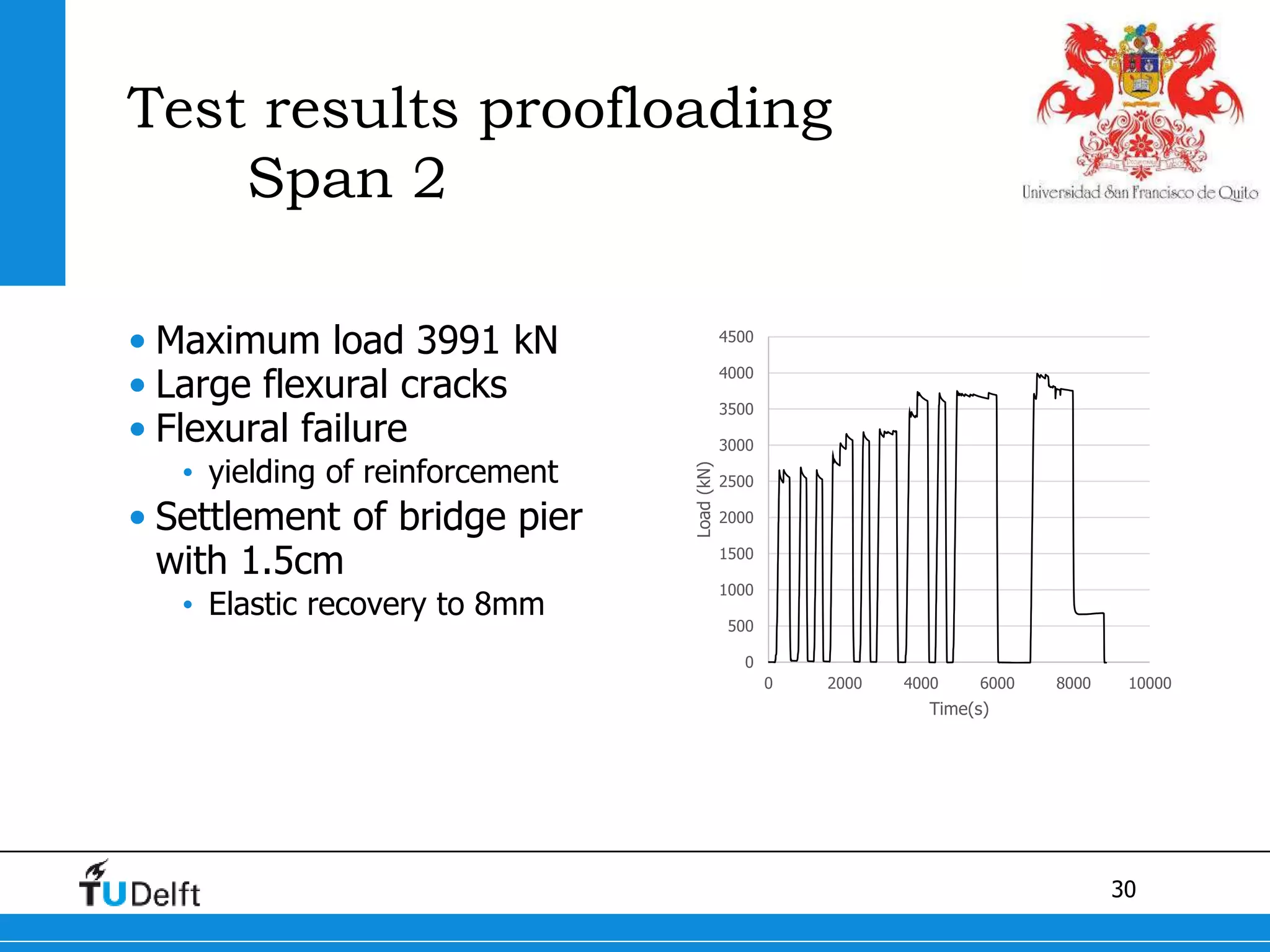
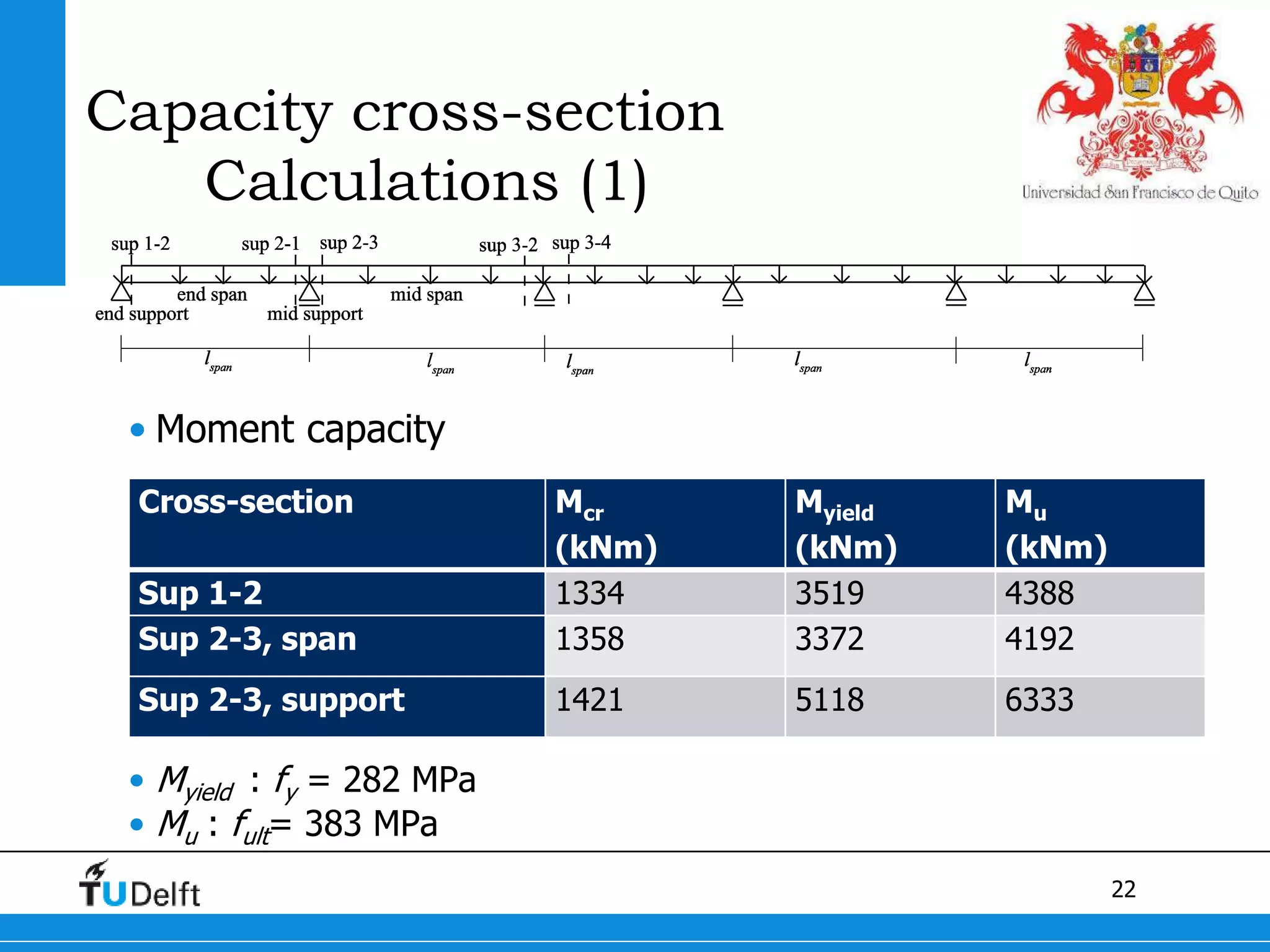
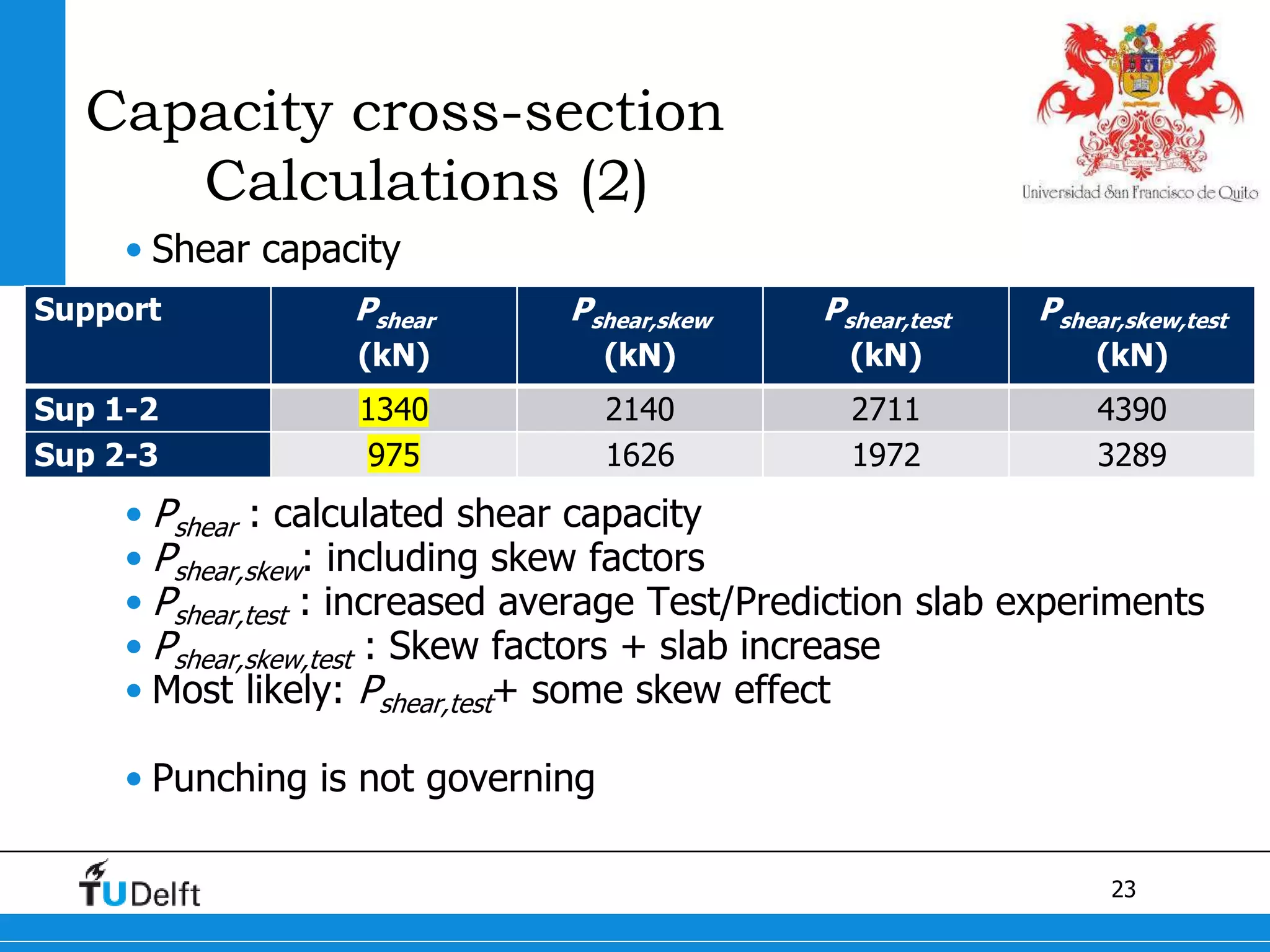
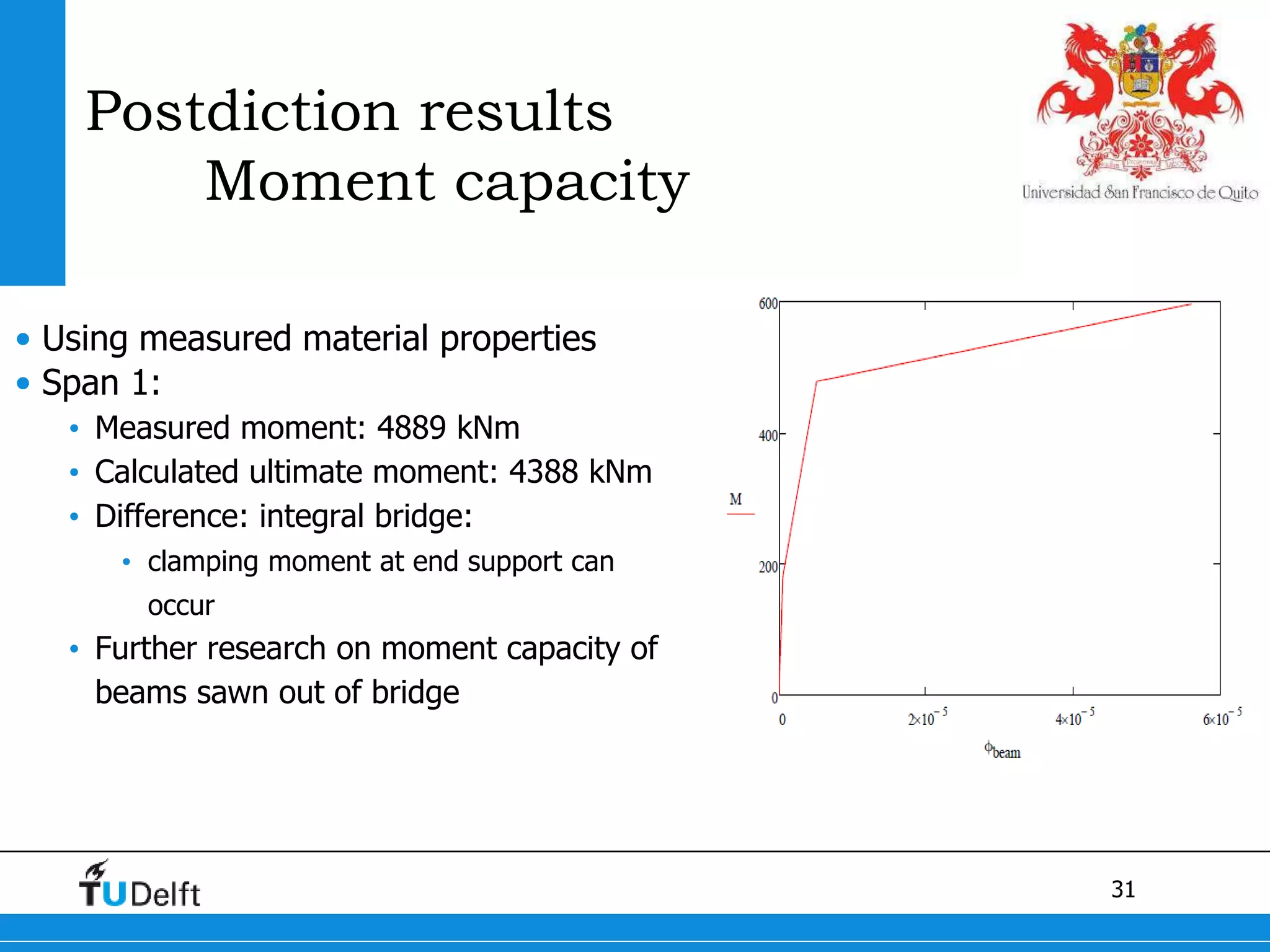
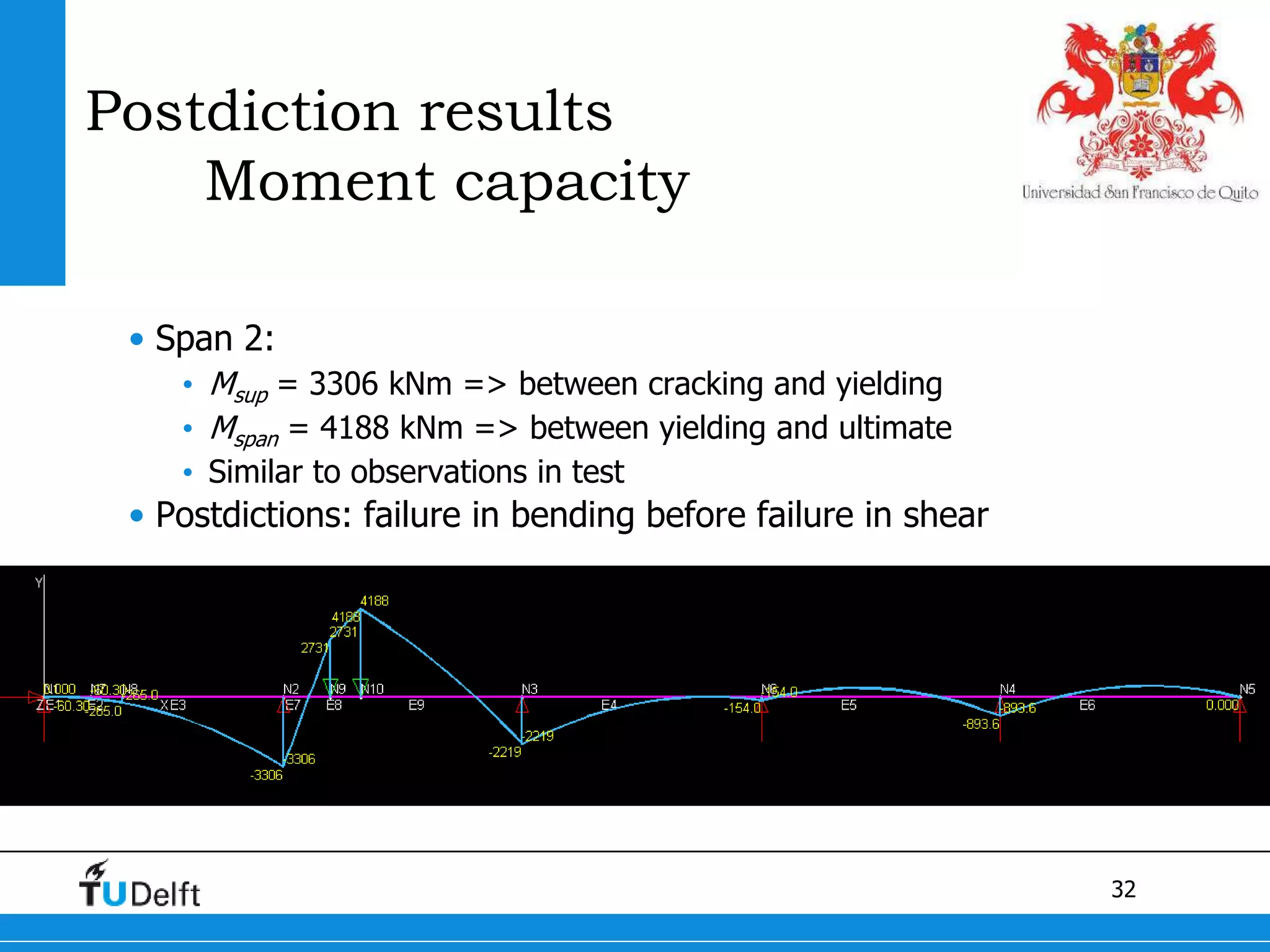
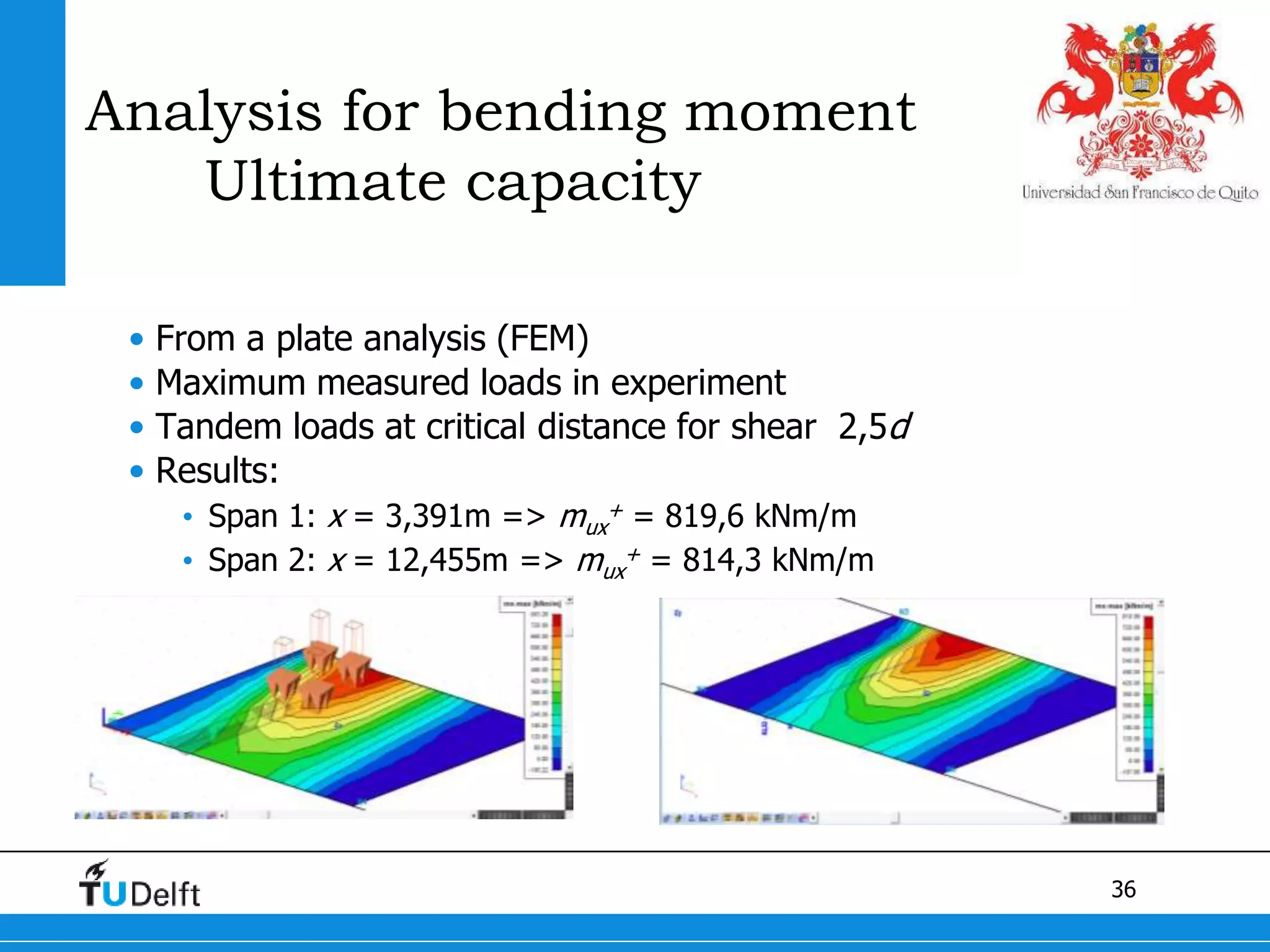
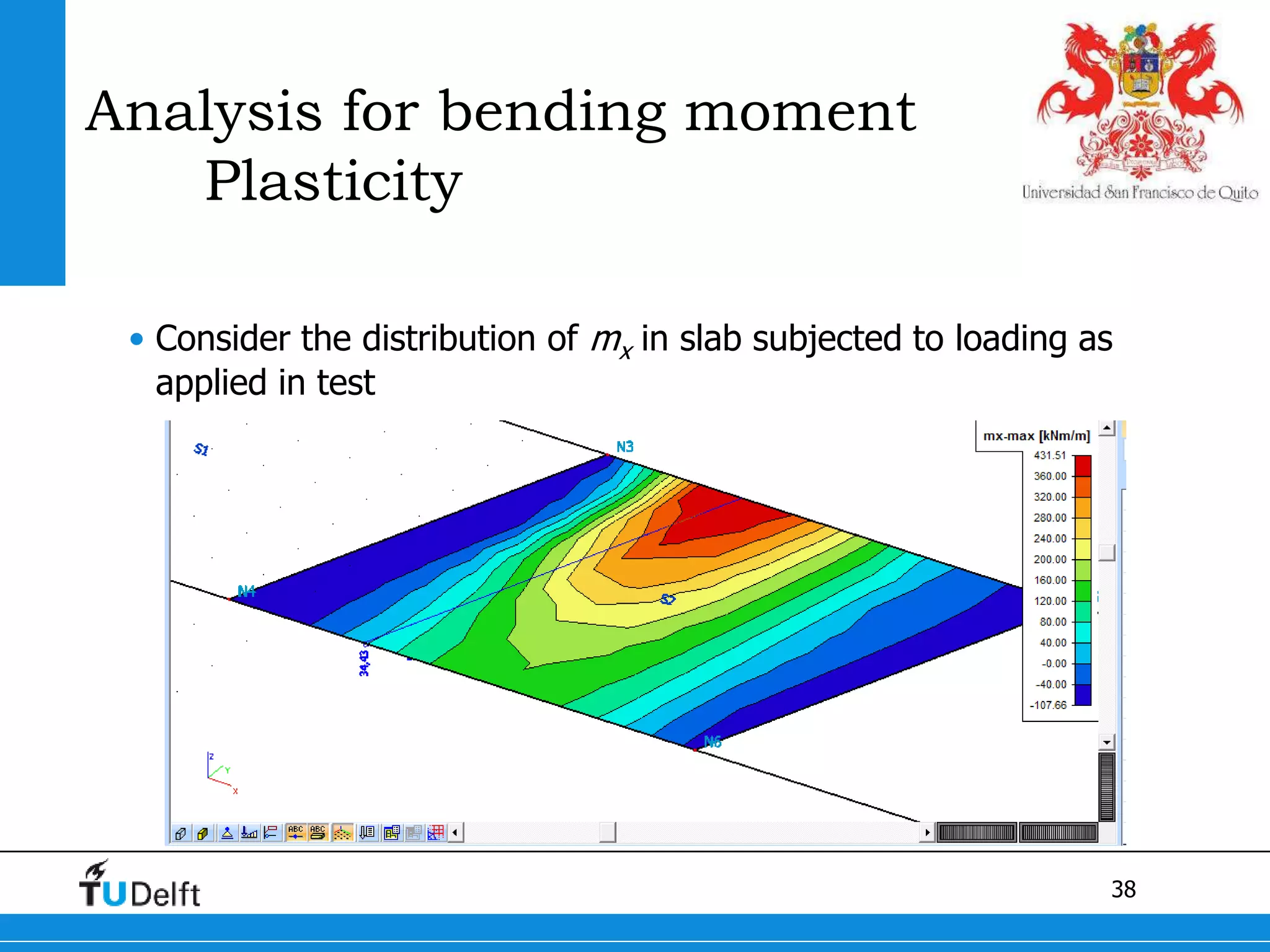
1) The Quick Scan analysis predicted failure by flexure in Span 1 and either flexure or shear failure in Span 2 of the Ruytenschildt Bridge. 2) Proofloading tests showed flexural cracking in Span 1 without failure, and flexural failure in Span 2 through yielding of reinforcement. 3) Postdiction analysis using material test results matched the failure modes observed and showed the bridge moments were below the calculated capacity.

1. Challenge the future
Delft
University of
Technology
Testing to Failure of the
Ruytenschildt Bridge
Analysis of the Ultimate Limit State Results
Eva Lantsoght, Cor van der Veen, Ane de Boer

2. 2
Overview
• Introduction to case
• Quick Scan predictions
• Predictions based on code equations
• Failure probability in shear vs flexure
• Test results
• Postdictions
• Conclusions
Slab shear experiments, TU Delft

3. 3
Proofloading
Case Ruytenschildtbrug
• Proofloading to assess capacity of
existing bridge
• ASR affected bridges
• Unaffected bridges
• Study cracks and deformations for
applied loads
• Crack formation: acoustic emissions
measurements
• Control load process
• Ruytenschildtbrug: testing to failure

4. 4
Proofloading Ruytenschildt Bridge
Existing bridge Partial demolition and building new bridge

5. 5
Proofloading
Case Ruytenschildtbrug

6. 6
Quick Scan approach
• Quick Scan shear behavior in slabs
• Similar to hand calculation
• In spreadsheet
• Developed since +- 2005
• Conservative approach
• First Level of Approximation
• Only relevant cross-sections of each span
• Includes results from slab shear tests TU
Delft
• Result = unity check = vEd/vRd,c

7. 7
Recommendations
Effective width
• Experiments on slabs with variable widths
• Statistical analysis ofVexp/VEC with beff1 and beff2
• NLFEA: stress distribution at support
• Lower bound: 4dl

8. 8
Recommendations
Slab factor 1.25
• Comparison test results and EN 1992-1-
1:2005
• Normal distribution
• Characteristic increase at least 1.25
• Combination of β = av /2dl and slab
factor 1.25
βnew = av /2.5dl
for 0.5dl ≤ av ≤ 2.5dl

9. 9
Recommendations
Superposition of loads
• Experiments on slabs with line load and concentrated load
• Superposition is a conservative assumption
• Concentrated load over effective width
• Line load over entire width

10. 10
Recommendations
Lower bound vmin
• Built before 1962: QR24 steel reinforcement
• fyk = 240 MPa
• Eurocode 2 vmin based on fyk = 500 MPa
3/2 1/2 1/2
min 0.772 ck ykv k f f 


11. 11
Quick Scan
Position tandems Load Model 1
Load spreading at line support
Distribution UDL first lane

12. 12
Quick Scan
Cross-sections –Ruytenschildt Bridge
• Cross-sections to check for 5-span beam
• Check sup 1-2, sup 2-1 and sup 2-3
• Testing in span 1 and span 2
• close to end support
• close to mid support

13. 13
Quick Scan development
QS-Excel-RWS
• more cross-sections
• Reinforcement more detailed
QS-MathCad-TUDelft

14. 14
Quick Scan Ruytenschildt Bridge
• Predictions: not all material parameters known beforehand
• Assume QR24 steel
• Some test results of concrete cores: compression and splitting
• Based on characteristic values
• Follows rating procedures
• Skew 72º angle
• Skew factors as used in QS
• Concrete compressive strength not known beforehand
• Calculations over range of compressive strengths
TS Edge distance Skew Factor For 0.7m
TS1 0.5m 1.08
1.084
0.95m 1.09
TS2 0.5m 1.23
1.239
0.95m 1.25

15. 15
Quick Scan Ruytenschildt Bridge
Support 1-2
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 10 20 30 40 50 60 70 80 90 100
unitycheck
fck,cube

16. 16
Quick Scan Ruytenschildtbrug
Support 2-3
0
0.2
0.4
0.6
0.8
1
1.2
0 10 20 30 40 50 60 70 80 90 100
unitycheck
fck,cube

17. 17
Capacity cross-section
Introduction
• Average material
• Two loading possibilities:
• Battens + big bags
• 4 wheel loads: simulating 1 load tandem
• Skew factors as in Quick Scan
• Saw cut at 7.365m over full length of bridge
• Average vRd,c
• Averagevmin : transform formula to average instead of
characteristic
3/2 1/2
1/2
1.08 0.163
0.12
ck
min
yk
k f
v
f


18. 18
Capacity cross-section
Selection loading scenario (1)
• Scenario 1: big bags sand + battens load
=> Flexural failure before shear failure
Effective width battens

19. 19
Capacity cross-section
Selection loading scenario (2)
• Scenario 2: only battens load + self-weight as distributed
load
=> Failure in flexure before shear

20. 20
Capacity cross-section
Selection loading scenario (3)
• Scenario 3: Wheel loads + self-weight
Flexural failure before shear failure in span 1
Possible shear failure in span 2

21. 21
Capacity cross-section
Effective width for skewed slab

22. 22
Capacity cross-section
Calculations (1)
• Moment capacity
• Myield : fy = 282 MPa
• Mu : fult= 383 MPa
Cross-section Mcr
(kNm)
Myield
(kNm)
Mu
(kNm)
Sup 1-2 1334 3519 4388
Sup 2-3, span 1358 3372 4192
Sup 2-3, support 1421 5118 6333

23. 23
Capacity cross-section
Calculations (2)
• Shear capacity
• Pshear : calculated shear capacity
• Pshear,skew: including skew factors
• Pshear,test : increased average Test/Prediction slab experiments
• Pshear,skew,test : Skew factors + slab increase
• Most likely: Pshear,test+ some skew effect
• Punching is not governing
Support Pshear
(kN)
Pshear,skew
(kN)
Pshear,test
(kN)
Pshear,skew,test
(kN)
Sup 1-2 1340 2140 2711 4390
Sup 2-3 975 1626 1972 3289

24. 24
Probability of shear failure
• Monte Carlo simulation
 shear < flexurefp P
( )f shear flexurep P UC UC 
 
 
1/3,
1/3
,
, , ,
100
100
Rd c
l ck
Ed c
shear
Rd c
Rd c test l c mean
C
k f
v
UC
Testv C k f
Predicted



 
2
2
s y
Ed
flexure
Rd
s u
M
a
A f d
M
UC
Test aM
A f d
Predicted
 
 
  
   
   
   

25. 25
Probability of shear failure
Test/Predicted shear
Based on slab shear experiments TU Delft

26. 26
Probability of shear failure
Limit state function

27. 27
Probability of shear failure
Results
• Span 1: 85.2% probability of failure in flexure before shear
• Span 2: 45.9% probability of failure in flexure before shear
• Span 2: 98.2% probability of failure in flexure before shear
when considering from
V
Test
Predicted
 
 
 
exp
pred
V
V

28. 28
Uncertainties in predictions
• Effect skew angle on effective
width
• Effect skew on shear capacity of
slabs
• Concrete compressive strength
(assumed B45)
• Yield strength of steel (fy = 282
MPa assumed)

29. 29
Test results proofloading
Span 1
• Maximum load 3049 kN
• Maximum available load for span 1
• Flexural cracks
• No failure
• Order additional load for test 2!
0
500
1000
1500
2000
2500
3000
3500
0 5000 10000 15000 20000 25000
Load(kN) time (s)

30. 30
Test results proofloading
Span 2
• Maximum load 3991 kN
• Large flexural cracks
• Flexural failure
• yielding of reinforcement
• Settlement of bridge pier
with 1.5cm
• Elastic recovery to 8mm
0
500
1000
1500
2000
2500
3000
3500
4000
4500
0 2000 4000 6000 8000 10000
Load(kN) Time(s)

31. 31
Postdiction results
Moment capacity
• Using measured material properties
• Span 1:
• Measured moment: 4889 kNm
• Calculated ultimate moment: 4388 kNm
• Difference: integral bridge:
• clamping moment at end support can
occur
• Further research on moment capacity of
beams sawn out of bridge

32. 32
Postdiction results
Moment capacity
• Span 2:
• Msup = 3306 kNm => between cracking and yielding
• Mspan = 4188 kNm => between yielding and ultimate
• Similar to observations in test
• Postdictions: failure in bending before failure in shear

33. 33
Analysis for bending moment
Finite element model
• Linear finite element model in Scia Engineer
• Concrete class C20/25 as based on tested cores
• Modeled as continuous slab, 5 spans
• Used for comparison between proofloading and Eurocode loads

34. 34
Analysis for bending moment
Largest moment with LM1
• Load Model 1 from Eurocode
• Self-weight + layer of asphalt
• Distributed lane load + concentrated
wheel loads
• Position of wheel loads resulting in
largest moment
• manual live load analysis
• Span 1: x = 4,633m => mux
+ = 438,5
kNm/m
• Span 2: x = 14,5m => mux
+ = 330,4
kNm/m

35. 35
Analysis for bending moment
Proofloading – Load levels
• Traditional proofloading:
• finish test before failure or damage to bridge
• load must pass “unfit for use” and “repair” levels
• identify these levels
• Requirement: same moment for EC load as for test tandem
• at “unfit for use” and “repair” load levels
• “Repair” level
• Span 1: axle load 620 kN, total load 1240 kN
• Span 2: axle load 544 kN, total load 1088 kN
• “Unfit for use” level
• Span 1: axle load 589 kN, total load 1178 kN
• Span 2: axle load 520 kN, total load 1040 kN

36. 36
Analysis for bending moment
Ultimate capacity
• From a plate analysis (FEM)
• Maximum measured loads in experiment
• Tandem loads at critical distance for shear 2,5d
• Results:
• Span 1: x = 3,391m => mux
+ = 819,6 kNm/m
• Span 2: x = 12,455m => mux
+ = 814,3 kNm/m

37. 37
Analysis for bending moment
Plasticity
• After yielding of reinforcement: formation of plastic hinge
• Analysis based on cracking pattern
• Analysis for span 2 (span 1: no failure)

38. 38
Analysis for bending moment
Plasticity
• Consider the distribution of mx in slab subjected to loading as
applied in test

39. 39
Analysis for bending moment
Plasticity
• Make a cut, find distribution of moments over width at position of
crack

40. 40
Analysis for bending moment
Plasticity
• Percentage of moment distributed over 3,63m (length of crack)?
• 77,4% of total moment in crack = plastic moment
• 22,6% remains linear elastic
• In linear elastic part: capacity can increase until reaching onset of
yielding and cracking
• Total moment due to maximum load: 2271 kNm

41. 41
Analysis for bending moment
Plasticity
• Linear elastic part carries moment after yielding and cracking:
• Can increase up to yield moment
3,735
77,39% 2271 1809
3,63
m
LEdeel kNm kNm
m
   
3,735
77,39% 2271
3,63
2852
m
LEdeel x kNm
m
x kNm
   
 

42. 42
Analysis for bending moment
Plasticity
• Maximum moment is thus 2852 kNm
• Corresponds to axle load of 1302 kN or total load of 2604 kN
• Additional capacity

43. 43
Conclusions
• Quick Scan: capacity fulfills
requirements for shear
• Predicted failure modes:
• Span 1: flexural failure
• Span 2: shear failure or flexural failure
• Experiments: proofloading
• Span 1: flexural failure (no failure in
experiment)
• Span 2: flexural failure
• Analysis of bending moment capacity
• Bridge OK according to proofloading levels
• Study of plasticity effects

44. 44
Contact:
Eva Lantsoght
E.O.L.Lantsoght@tudelft.nl // elantsoght@usfq.edu.ec
+31(0)152787449