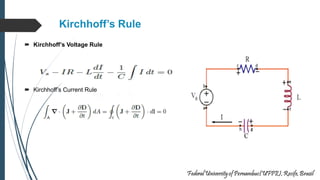
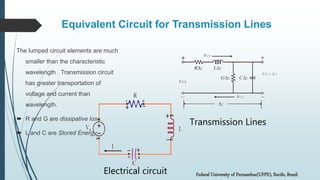
This document discusses transmission lines and their equivalent circuits. It introduces Kirchhoff's rules for analyzing transmission line segments. A lossless plane-parallel transmission line model is presented. Reflection on lossless terminated transmission lines is analyzed. Special termination cases are explored, including shorted lines where current is maximum and open lines where voltage is maximum. The impedance of lines at half-wave and quarter-wave points is also examined.

1. Transmission Lines and Equivalent
Circuits
By
Maryam Liaqat
Federal University of Pernambuc(UFPE), Recife, Brazil

2. Contornos
 Elemento Teoria do Circuito
 Regra Kirchoff
 Circuito Equivalente para linhas de trasmissão
 Análisa linhas de Transmissão
 Linhas de transmissão sem perdas plano paralales
 Reflxão sobre a perda menos linhas encerrada
 Casos especiais denúncia

3. Elementos Agrupados
 Resistancia
 Capacitor
 Indutor
Elemento Teoria do Circuito
• Electric effect happens instantaniously throughout the Circuit
• Net Charge of Circuit is null
• Megnatic Coupling among lumped components is negligible

4. Kirchhoff’s Rule
 Kirchhoff’s Voltage Rule
 Kirchhoff’s Current Rule

5. Equivalent Circuit for Transmission Lines
The lumped circuit elements are much
smaller than the characteristic
wavelength . Transmission circuit
has greater transportation of
voltage and current than
wavelength.
 R and G are dissipative loss.
 L and C are Stored Energy.
Transmission Lines
Electrical circuit Federal University of Pernambuc(UFPE), Recife, Brazil

6. Analysis of Transmission lines Segments by
Kirchhoff’s Rules
 From Voltage Rule

7.  From Current Rule

8. Lossless Plane-Parallel Transmission Line
Inductance per unit length can be calculated by Faraday’s
Law and current through a conductor plate can be
calculated by Maxwell-Ampere’s Law

9. Reflection on Lossless Terminated Line
 ZL is the load impedance across the line
conductors
 At Z=0,

10. Transmission line impedance
Zline (-d) with line terminated by
load ZL≠Z0.

11. Special Termination Cases
 Shorted Transmission Line ( ZL=0)
 Open Circuit Transmission Line (Zl= infinit)
 Line Impedance at d=-lamb/2
 Line Impedance at d=lamb./4

12. Shorted Transmission Line ( ZL=0)
At ZL=0 , the reflection coefficient is unity therefore the Zline is dependent only
on the distance and characteristic impedance. The Current is maximum in
this case but voltage is nullify.

13. Open Circuit Transmission Line (Zl= infinit)
In open circuit the load is completely removed and therefore reflection
coefficient is -1 and the Zline is exactly opposite to the shorted terminated
lines. Voltage is maximum at the point of load and current is null

14. Line Impedance at d=lamb/2 and at d=lamb./4
 At half-wave point, Zline is equal to ZL and independent of transmission line
characteristics
 Quarter-wave transformation can be used for the length of the line ( lamb/4) with
impedance Z1 (quarter-wave transformer) to match the input transmission line of
Impedance Z0 to the given load ZL. Here reflaction co-efficient is zero therefore