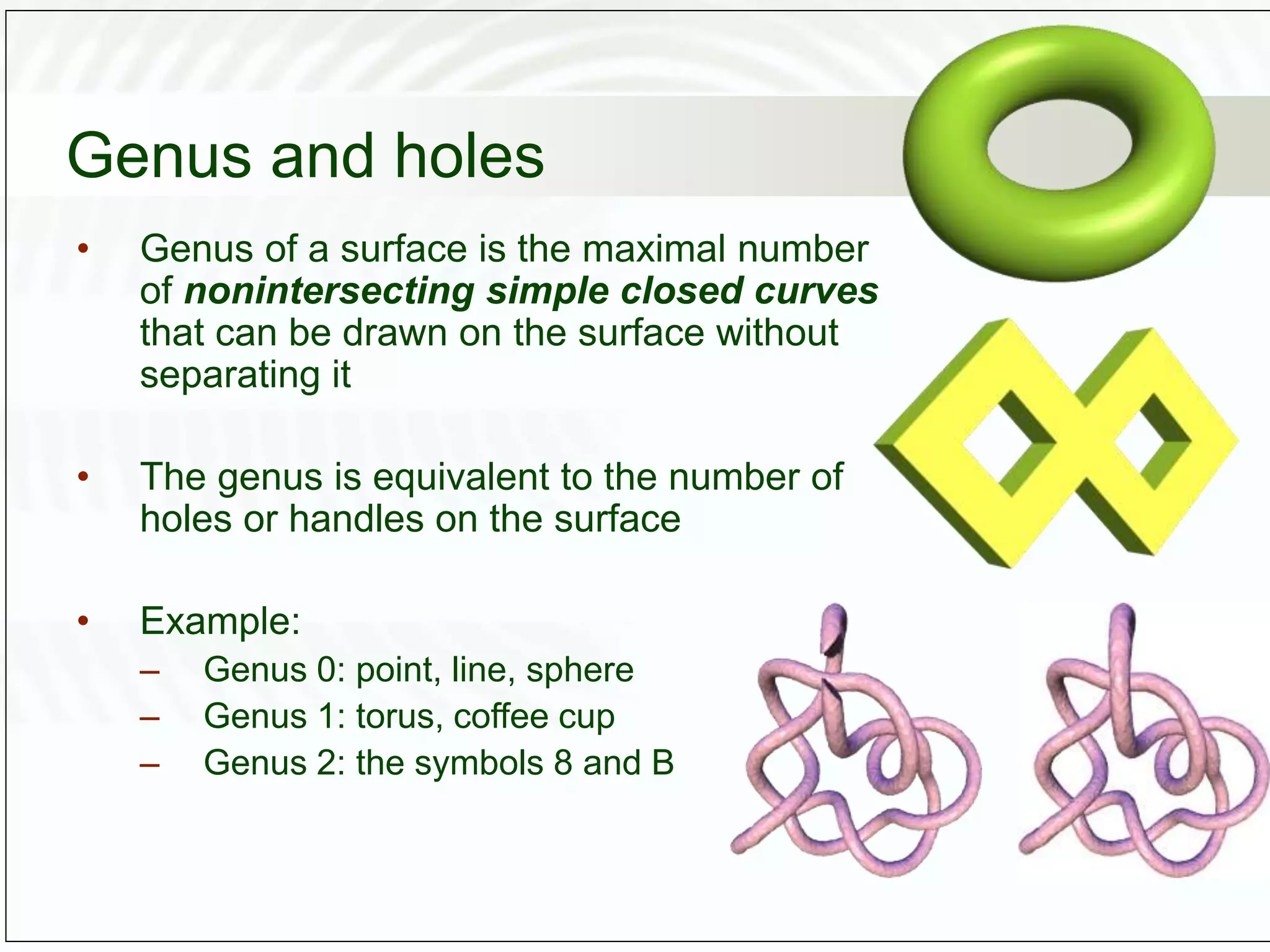
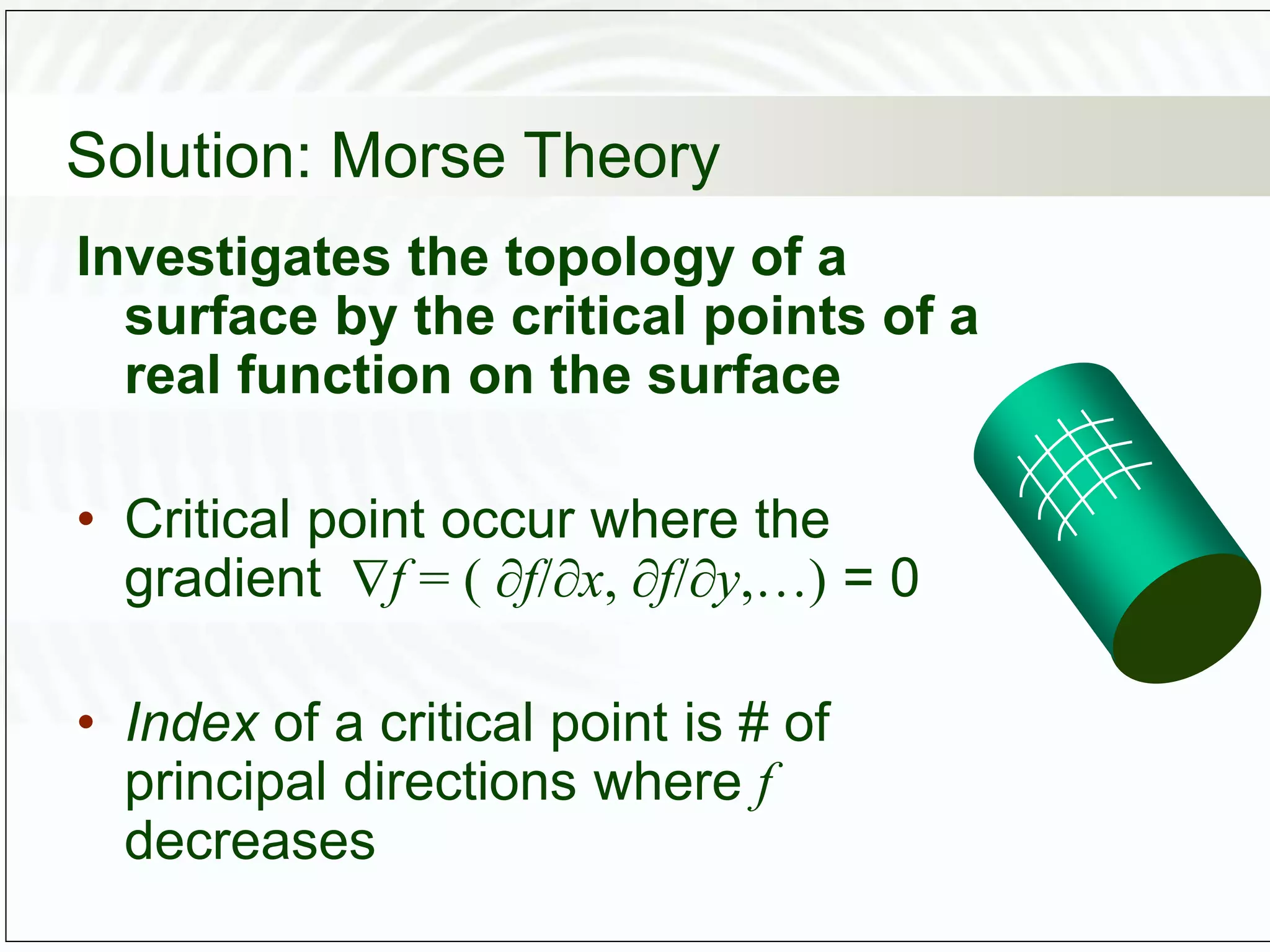
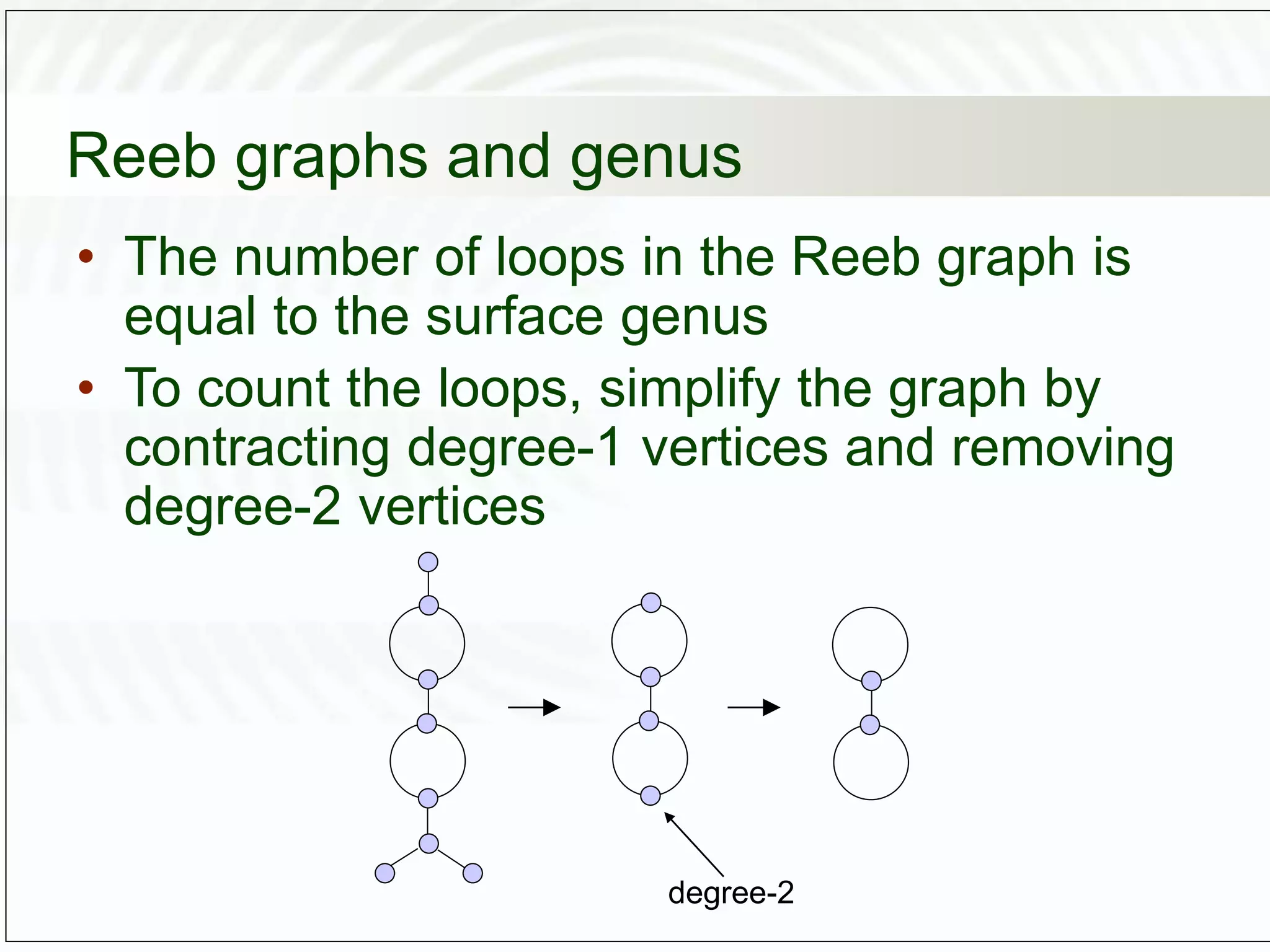
This document discusses computational topology and its applications in computer graphics. It introduces key concepts in topology such as homeomorphisms, genus, orientability, and Morse theory. Topology studies properties of shapes that are preserved under continuous deformations. Morse theory analyzes the topology of a surface by investigating the critical points of functions defined on the surface, such as the height function. Reeb graphs provide a way to schematically represent a Morse function and reveal topological properties of the shape like its genus. Computational topology techniques can be used for applications like shape matching, surface reconstruction from point clouds, and mesh partitioning.

1. Computational Topology
for
Computer Graphics
Klein bottle

2. What is Topology?
• The topology of a space is the definition of
a collection of sets (called the open sets)
that include:
– the space and the empty set
– the union of any of the sets
– the finite intersection of any of the sets
• “Topological space is a set with the least
structure necessary to define the
concepts of nearness and continuity”

3. No, Really.What is Topology?
• The study of properties of a shape that do not
change under deformation
• Rules of deformation
– Onto (all of A  all of B)
– 1-1 correspondence (no overlap)
– bicontinuous, (continuous both ways)
– Can’t tear, join, poke/seal holes
• A is homeomorphic to B

4. Why Topology?
• What is the boundary of an object?
• Are there holes in the object?
• Is the object hollow?
• If the object is transformed in some way, are the
changes continuous or abrupt?
• Is the object bounded, or does it extend infinitely
far?

5. Why Do We (CG) Care?
The study of connectedness
• Understanding
How connectivity happens?
• Analysis
How to determine connectivity?
• Articulation
How to describe connectivity?
• Control
How to enforce connectivity?

6. For Example
How does connectedness affect…
• Morphing
• Texturing
• Compression
• Simplification

7. Problem: Mesh Reconstruction
• Determines
shape from
point samples
• Different
coordinates,
different
shapes

8. Topological Properties
• To uniquely determine the type of
homeomorphism we need to know :
– Surface is open or closed
– Surface is orientable or not
– Genus (number of holes)
– Boundary components

9. Surfaces
• How to define “surface”?
• Surface is a space which ”locally
looks like” a plane:
– the set of zeroes of a polynomial
equation in three variables in R3 is a
2D surface: x2+y2+z2=1

10. Surfaces and Manifolds
• An n-manifold is a topological space
that “locally looks like” the Euclidian
space Rn
– Topological space: set properties
– Euclidian space: geometric/coordinates
• A sphere is a 2-manifold
• A circle is a 1-manifold

11. Open vs. Closed Surfaces
• The points x having a
neighborhood homeomorphic to
R2 form Int(S) (interior)
• The points y for which every
neighborhood is homeomorphic to
R2
0 form ∂S (boundary)
• A surface S is said to be closed if
its boundary is empty

12. Orientability
• A surface in R3 is called orientable, if it
is possible to distinguish between its
two sides (inside/outside above/below)
• A non-orientable surface has a path
which brings a traveler back to his
starting point mirror-reversed (inverse
normal)

13. Orientation by Triangulation
• Any surface has a triangulation
• Orient all triangles CW or CCW
• Orientability: any two triangles
sharing an edge have opposite
directions on that edge.

14. Genus and holes
• Genus of a surface is the maximal number
of nonintersecting simple closed curves
that can be drawn on the surface without
separating it
• The genus is equivalent to the number of
holes or handles on the surface
• Example:
– Genus 0: point, line, sphere
– Genus 1: torus, coffee cup
– Genus 2: the symbols 8 and B

15. Euler characteristic function
• Polyhedral decomposition of a surface
(V = #vertices, E = #edges, F = #faces)
(M) = V – E + F
– If M has g holes and h boundary components then
(M) = 2 – 2g – h
–(M) is independent of the polygonization
 = 1  = 2  = 0

16. Summary: equivalence in R3
• Any orientable closed surface
is topologically equivalent to a
sphere with g handles
attached to it
– torus is equivalent to a sphere
with one handle ( =0, g=1)
– double torus is equivalent to a
sphere with two handles ( =-2 ,
g=2)

17. Hard Problems… Dunking a Donut
• Dunk the donut in
the coffee!
• Investigate the
change in topology
of the portion of the
donut immersed in
the coffee

23. Solution: Morse Theory
Investigates the topology of a
surface by the critical points of a
real function on the surface
• Critical point occur where the
gradient f = (f/x, f/y,…) = 0
• Index of a critical point is # of
principal directions where f
decreases

24. Example: Dunking a Donut
• Surface is a torus
• Function f is height
• Investigate topology of f  h
• Four critical points
– Index 0 : minimum
– Index 1 : saddle
– Index 1 : saddle
– Index 2 : maximum
• Example: sphere has a function with only critical
points as maximum and a minimum

25. How does it work? Algebraic Topology
• Homotopy equivalence
– topological spaces are varied, homeomorphisms
give much too fine a classification to be useful…
• Deformation retraction
• Cells

26. Homotopy equivalence
• A ~ B  There is a continuous map between A
and B
• Same number of components
• Same number of holes
• Not necessarily the same dimension
• Homeomorphism Homotopy
~ ~


27. Deformation Retraction
• Function that continuously reduces a set
onto a subset
• Any shape is homotopic to any of its
deformation retracts
• Skeleton is a deformation retract of the
solids it defines
~ ~ ~
~

28. Cells
• Cells are dimensional primitives
• We attach cells at their boundaries
0-cell 1-cell 2-cell 3-cell

29. Morse function
• f doesn’t have to be height – any Morse
function would do
• f is a Morse function on M if:
– f is smooth
– All critical points are isolated
– All critical points are non-degenerate:
• det(Hessian(p)) != 0
2 2
2
2 2
2
( ) ( )
( )
( ) ( )
f f
x x y
Hessian f
f f
y x y
 
 
 
  
 

 
 
 
 
  
 
p p
p
p p

30. Critical Point Index
• The index of a critical point is the number of
negative eigenvalues of the Hessian:
– 0  minimum
– 1  saddle point
– 2  maximum
• Intuition: the number
of independent
directions in which
f decreases ind=0
ind=1
ind=1
ind=2

31. If sweep doesn’t pass critical point
[Milnor 1963]
• Denote Ma
= {p  M | f(p)  a} (the sweep
region up to value a of f )
• Suppose f 1
[a, b] is compact and doesn’t
contain critical points of f. Then Ma
is
homeomorphic to Mb
.

32. Sweep passes critical point
[Milnor 1963]
• p is critical point of f with index ,  is
sufficiently small. Then Mc+
has the same
homotopy type as Mc
with -cell attached.
Mc
Mc+
Mc Mc
with -cell
attached
~
Mc+

33. This is what happened to the doughnut…

34. What we learned so far
• Topology describes properties of shape that
are invariant under deformations
• We can investigate topology by
investigating critical points of Morse
functions
• And vice versa: looking at the topology of
level sets (sweeps) of a Morse function, we
can learn about its critical points

35. Reeb graphs
• Schematic way to present a Morse function
• Vertices of the graph are critical points
• Arcs of the graph are connected components of
the level sets of f, contracted to points
2
1
1
1
1
1
0 0

36. Reeb graphs and genus
• The number of loops in the Reeb graph is
equal to the surface genus
• To count the loops, simplify the graph by
contracting degree-1 vertices and removing
degree-2 vertices
degree-2

37. Another Reeb graph example

38. Discretized Reeb graph
• Take the critical points and “samples” in
between
• Robust because we know that nothing
happens between consecutive critical points

39. Reeb graphs for Shape Matching
• Reeb graph encodes the behavior of a
Morse function on the shape
• Also tells us about the topology of the
shape
• Take a meaningful function and use its
Reeb graph to compare between shapes!

40. Choose the right Morse function
• The height function f (p) = z is not good
enough – not rotational invariant
• Not always a Morse function

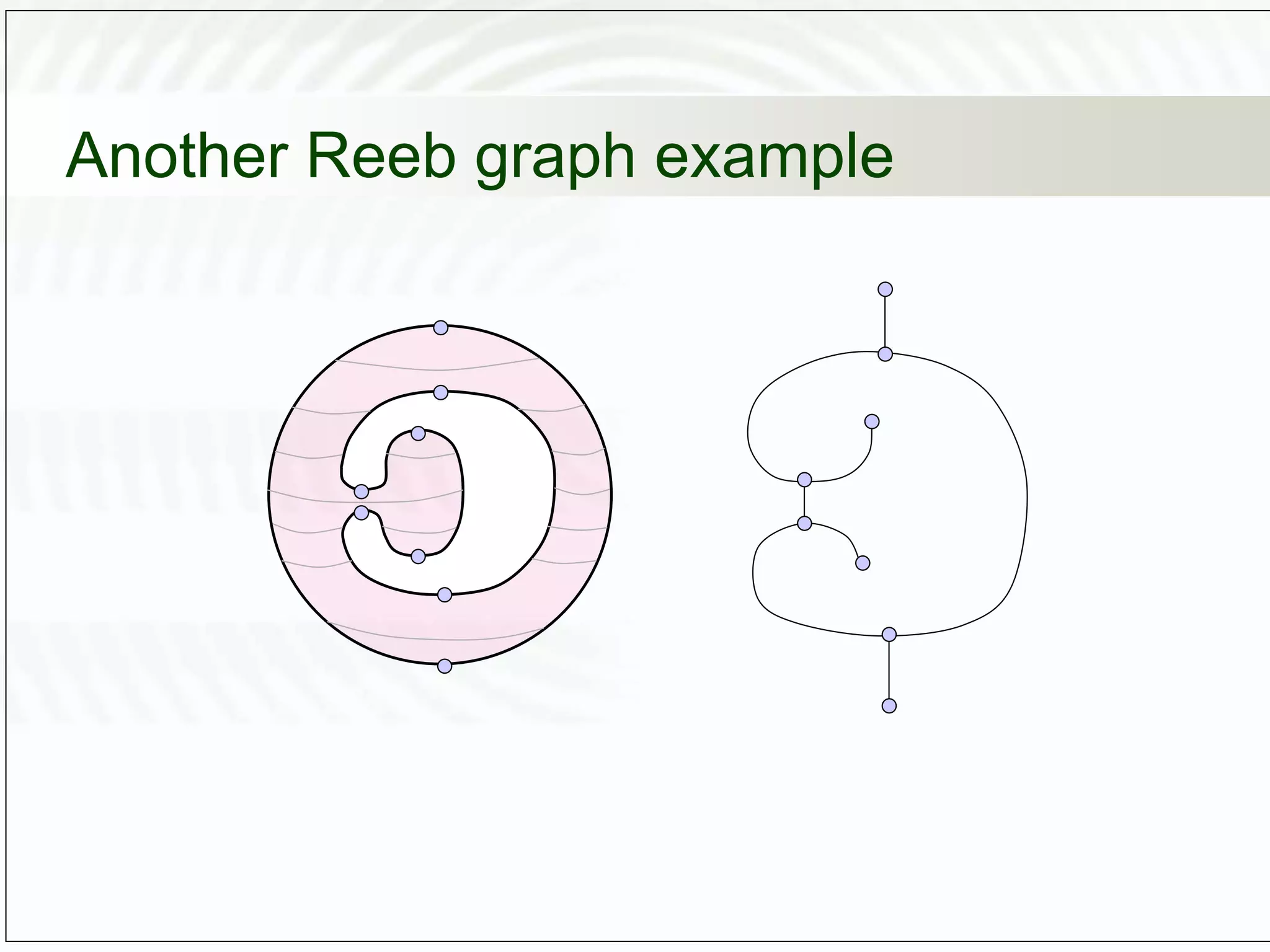
41. Average geodesic distance
• The idea of [Hilaga et al. 01]: use geodesic
distance for the Morse function!
( ) geodist( , )
( ) min ( )
( )
max ( )
M
M
M
g dS
g g
f
g






q
q
p p q
p q
p
q

42. Multi-res Reeb graphs
• Hilaga et al. use multiresolutional Reeb
graphs to compare between shapes
• Multiresolution hierarchy – by gradual
contraction of vertices

43. Mesh Partitioning
• Now we get to [Zhang et al. 03]
• They use almost the same f as [Hilaga et al.
01]
• Want to find features = long protrusions
• Find local maxima of f !

44. Region growing
• Start the sweep from global minimum
(central point of the shape)
• Add one triangle at a time – the one with
smallest f
• Record topology changes in the boundary
of the sweep front – these are critical points

45. Critical points – genus-0 surface
• Splitting saddle – when the front splits into two
• Maximum – when one front boundary component
vanishes
max max
splitting
saddle
min