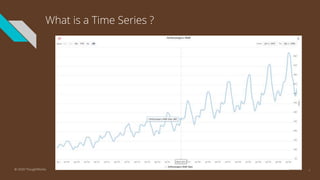
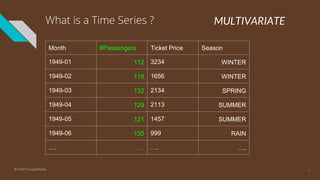
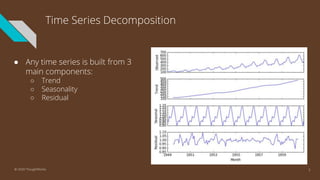
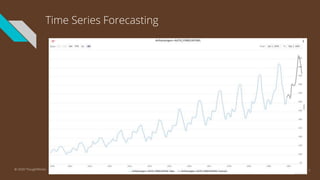
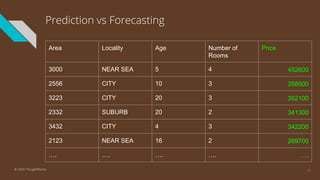
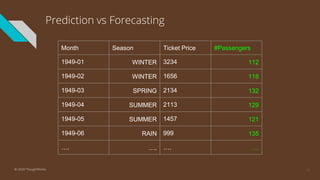
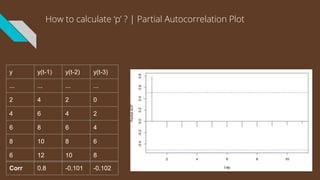
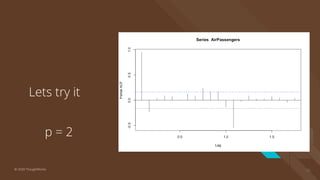
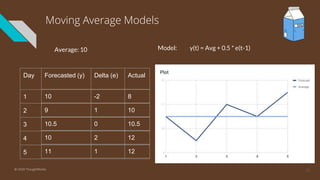
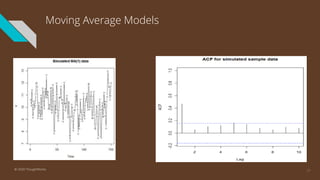
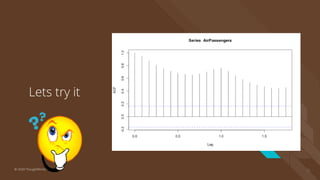
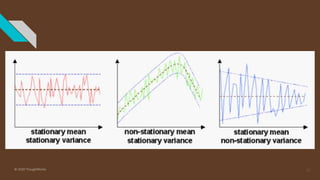
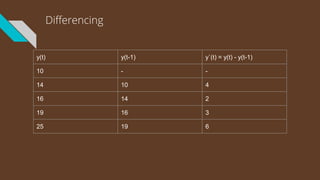
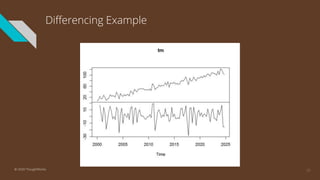
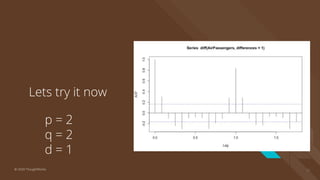
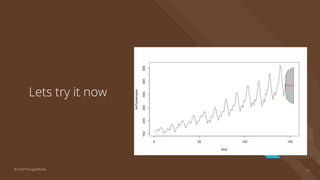
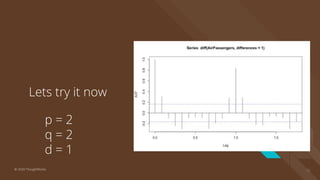
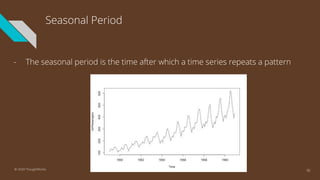
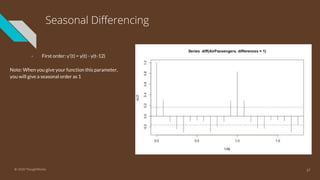
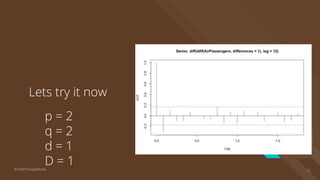
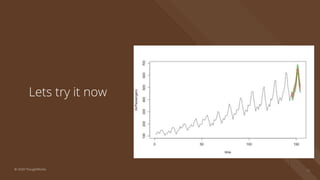
The document provides an introduction to time series analysis, detailing its components, forecasting techniques, and specific models within the ARIMA family. Key concepts include the distinction between univariate and multivariate time series, seasonal components, and the need for stationarity in models. Various forecasting methods such as AR, MA, ARMA, and SARIMA are discussed alongside practical examples of time series forecasting applications.