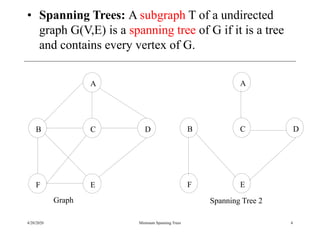
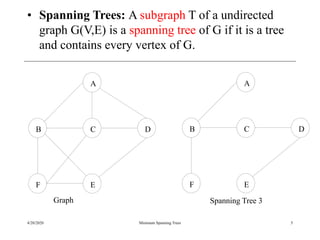
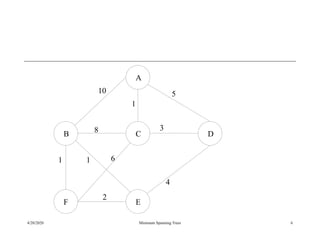
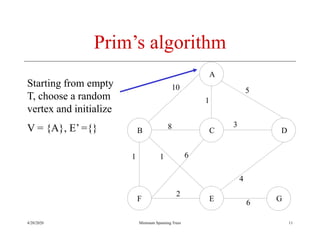
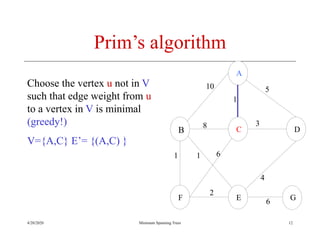
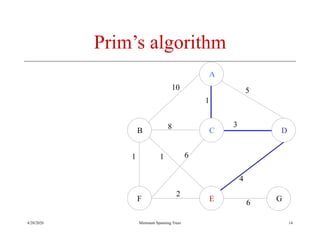
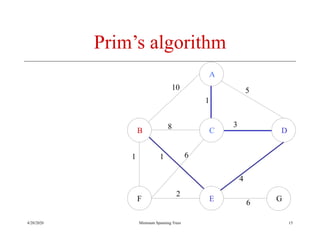
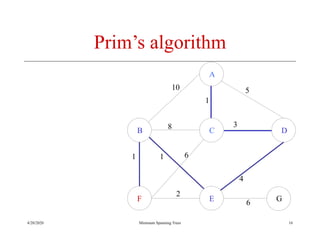
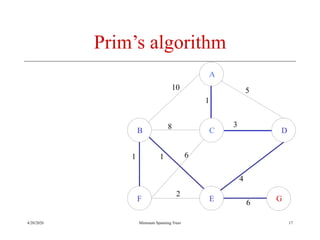
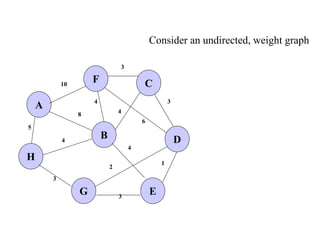
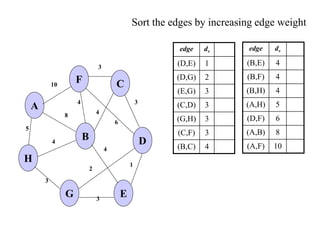
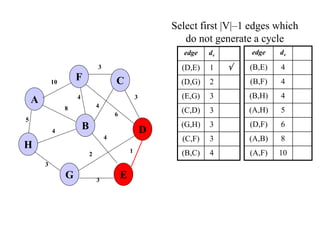
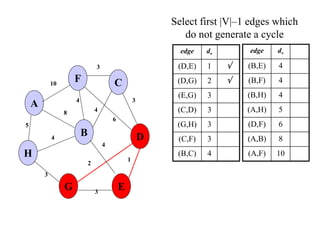
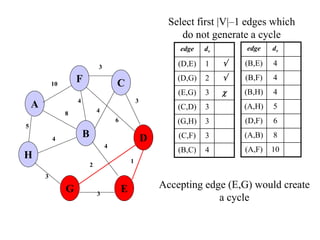
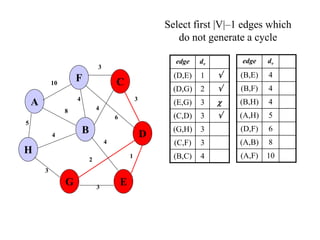
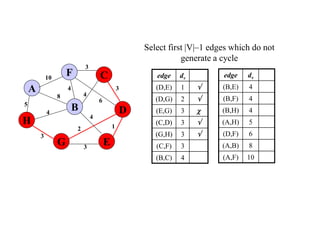
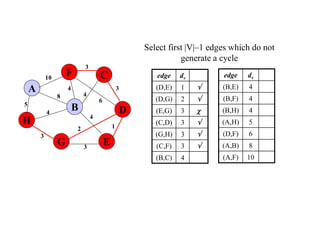
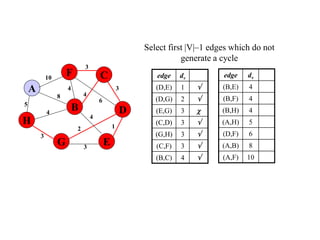
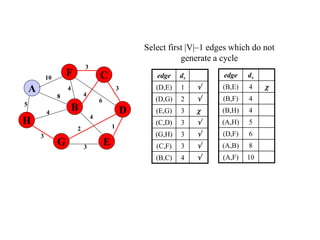
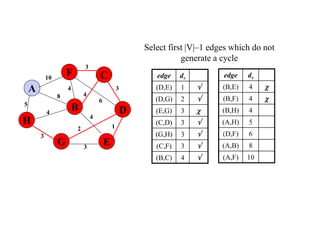
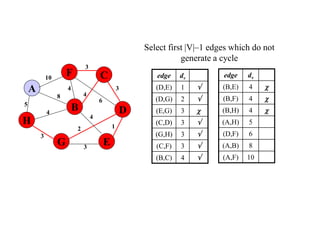
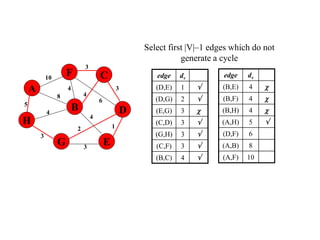
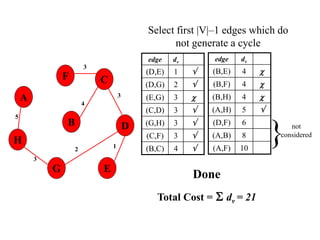
The document discusses spanning trees and minimum spanning trees. It introduces Prim's algorithm and Kruskal's algorithm for finding minimum spanning trees in weighted graphs. Prim's algorithm builds the minimum spanning tree incrementally by adding edges connected to the partial tree, while Kruskal's algorithm sorts the edges by weight and adds edges in order while avoiding cycles.

1. • Spanning Trees
• Minimum Spanning Trees
 Prim’s algorithm
Kruskal’s Algorithm
• Huffman Coding

2. 4/20/2020 Minimum Spanning Trees
Spanning Trees
• Given (connected) graph G(V,E),
a spanning tree T(V’,E’):
› Is a subgraph of G; that is, V’  V, E’  E.
› Spans the graph (V’ = V)
› Forms a tree (no cycle);
› So, E’ has |V| -1 edges
2

3. • Spanning Trees: A subgraph T of an undirected
graph G(V,E) is a spanning tree of G if it is a tree
and contains every vertex of G.
4/20/2020 Minimum Spanning Trees 3
A
B C D
F E
A
B C D
F E
Spanning Tree 1
Graph

4. • Spanning Trees: A subgraph T of a undirected
graph G(V,E) is a spanning tree of G if it is a tree
and contains every vertex of G.
4/20/2020 Minimum Spanning Trees 4
A
B C D
F E
A
B C D
F E
Graph Spanning Tree 2

5. • Spanning Trees: A subgraph T of a undirected
graph G(V,E) is a spanning tree of G if it is a tree
and contains every vertex of G.
4/20/2020 Minimum Spanning Trees 5
A
B C D
F E
Graph
A
B C D
F E
Spanning Tree 3

6. 4/20/2020 Minimum Spanning Trees 6
A
B C D
F E
10
1
5
8 3
1 1 6
2
4

7. 4/20/2020 Minimum Spanning Trees
Minimum Spanning Trees
• Edges are weighted: find minimum weight
spanning tree
• Applications
› Find cheapest way to wire your house
› Find minimum cost to send messages on the
Internet
7

8. 4/20/2020 Minimum Spanning Trees
Strategy for Minimum Spanning
Tree
• For any spanning tree T, inserting an edge
enew not in T creates a cycle
• But
› Removing any edge eold from the cycle gives
back a spanning tree
› If enew has a lower cost than eold we have
progressed!
8

9. 4/20/2020 Minimum Spanning Trees
Strategy
• Strategy for construction:
› Add an edge of minimum cost that does not
create a cycle (greedy algorithm)
› Repeat |V| -1 times
› Correct since if we could replace an edge with
one of lower cost, the algorithm would have
picked it up
9

10. 4/20/2020 Minimum Spanning Trees
Two Algorithms
1. Prim: (build tree incrementally)
› Pick minimum weight edge connected to known
(incomplete) spanning tree that does not create a cycle
and expand to include it in the tree
10

11. 4/20/2020 Minimum Spanning Trees
Prim’s algorithm
Starting from empty
T, choose a random
vertex and initialize
V = {A}, E’ ={}
A
B C D
F E
10
1
5
8 3
1 1 6
2
4
6 G
11

12. 4/20/2020 Minimum Spanning Trees
Prim’s algorithm
Choose the vertex u not in V
such that edge weight from u
to a vertex in V is minimal
(greedy!)
V={A,C} E’= {(A,C) }
A
B C D
F E
10
1
5
8 3
1 1 6
2
4
G6
12

13. 4/20/2020 Minimum Spanning Trees
Prim’s algorithm
Repeat until all vertices have been chosen
Choose the vertex u not in V such that
edge weight from v to a vertex in V is
minimal (greedy!)
V= {A,C,D} E’= {(A,C),(C,D)}
V={A,C,D,E} E’={(A,C),(C,D),(D,E)}
……
…….
………
A
B C D
F E
10
1
5
8 3
1 1 6
2
4
6 G
13

14. 4/20/2020 Minimum Spanning Trees
Prim’s algorithm
A
B C D
F E
10
1
5
8 3
1 1 6
2
4
6 G
14

15. 4/20/2020 Minimum Spanning Trees
Prim’s algorithm
A
B C D
F E
10
1
5
8 3
1 1 6
2
4
6 G
15

16. 4/20/2020 Minimum Spanning Trees
Prim’s algorithm
A
B C D
F E
10
1
5
8 3
1 1 6
2
4
6 G
16

17. 4/20/2020 Minimum Spanning Trees
Prim’s algorithm
A
B C D
F E
10
1
5
8 3
1 1 6
2
4
6 G
17

18. 4/20/2020 Minimum Spanning Trees
Prim’s algorithm
Repeat until all vertices have been
selected
V={A,C,D,E,B,F,G}
E’={(A,C),(C,D),(D,E),
(E,B),(B,F),(E,G)}.
Final Cost: 1 + 3 + 4 + 1 + 1 + 6 =
16
A
B C D
F E
10
1
5
8 3
1 1 6
2
4
6 G
18

19. 4/20/2020 Minimum Spanning Trees
Prim’s algorithm Analysis
• If the “Select the unmarked node u with minimum cost” is
done with binary heap then
O((|V|+|E|)log |V|)
19

20. 4/20/2020 Minimum Spanning Trees
Two Algorithms
1. Prim: (build tree incrementally)
› Pick minimum weight edge connected to known
(incomplete) spanning tree that does not create a cycle
and expand to include it in the tree
2. Kruskal: (build tree on sorted edges)
› Pick minimum weight edge not yet in a tree that does
not create a cycle. Then expand the set of included
edges to include it.
20

21. 4/20/2020 Minimum Spanning Trees
Kruskal’s Algorithm
1.Sort all the edges in non-decreasing order of
their weight.
2.Pick the smallest edge. Check if it forms a
cycle with the spanning tree formed so far. If
cycle is not formed, include this edge. Else,
discard it.
3.Repeat step#2 until there are (V-1) edges in
the spanning tree.
21

22. Consider an undirected, weight graph
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10

23. Sort the edges by increasing edge weight
edge dv
(D,E) 1
(D,G) 2
(E,G) 3
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10
edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

24. Select first |V|–1 edges which
do not generate a cycle
edge dv
(D,E) 1 
(D,G) 2
(E,G) 3
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10
edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

25. Select first |V|–1 edges which
do not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10
edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

26. Select first |V|–1 edges which
do not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10
edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Accepting edge (E,G) would create
a cycle

27. Select first |V|–1 edges which
do not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10
edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

28. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

29. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

30. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4 
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

31. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4 
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

32. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4 
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 
(B,F) 4 
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

33. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4 
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 
(B,F) 4 
(B,H) 4 
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

34. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4 
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 
(B,F) 4 
(B,H) 4 
(A,H) 5 
(D,F) 6
(A,B) 8
(A,F) 10

35. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4 
edge dv
(B,E) 4 
(B,F) 4 
(B,H) 4 
(A,H) 5 
(D,F) 6
(A,B) 8
(A,F) 10
Done
Total Cost =  dv = 21
5
1
A
H
B
F
E
D
C
G
2
3
3
3
4
} not
considered

36. 4/20/2020 Minimum Spanning Trees
Properties of trees in K’s
algorithm
• Trees form equivalent classes under the relation
“is connected to”
› u connected to u (reflexivity)
› u connected to v implies v connected to u (symmetry)
› u connected to v and v connected to w implies a path
from u to w so u connected to w (transitivity)
36