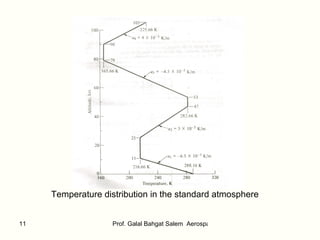
The document summarizes the structure and properties of the standard atmosphere model used in aerospace engineering. It describes the standard atmosphere as divided into layers of either constant temperature or linear temperature gradients. Equations are provided to calculate how pressure, temperature, and density vary with altitude based on the temperature profile and hydrostatic equation. Standard atmosphere tables in appendices provide mean property values as a function of altitude that serve as a reference for aircraft and vehicle design and performance calculations.

1. Chapter 3 The Standard Atmosphere 1.Structure Of The Atmosphere ● Atmosphere is the air envelope surrounding the earth ● Air is a mixture of several gases, where Oxygen represents (21%) ,Nitrogen (78%), and other gases (1%) of the total volume. ● Up to about 90 km altitude, composition of air is the same (the homosphere ( ● Above about 90 km, composition varies with altitude (the heterosphere) as shown in figure.

3. ● The atmosphere is divided into several layers according to temperature variation with altitude Why do we study the atmosphere? ● For the design and performance determination of any flying vehicle (airplane, missile, satellite,….etc), knowledge of the vertical distribution of pressure, temperature, and density of air is required. ● The properties of the real atmosphere never remain constant at any particular time or place. ● Consequently, a hypothetical model is employed as an approximation to what may be expected. This model is known as the standard atmosphere .

4. The Standard atmosphere depends on the measurement of the mean value of temperature with altitude combined with the hydrostatic equation which gives the variation of p with the altitude . 2.The Hydrostatic Equation Force diagram for the hydrostatic equation Fluid element of air at rest +ve h G

5. For equilibrium of the air element, the some of the forces in any direction must be zero. Resolving in the vertical direction: p(1)(1) – (p+dp)(1)(1) – ρ (1)(1) g dh G = 0 Then - dp – ρ g dh G = 0 Or dp/dh G = - ρ g Hydrostatic equation This equation means that the pressure decreases with the increase of height.

6. What is the altitude? ● There are six (6) different altitudes: 1-Geometric Altitude h G is the height above sea-level. 2-Absolute Altitude h a is the height measured from the center of the earth. h a = h G + R where R is the radius of earth ( R = 6356.766 km) The absolute altitude is important for space flight because g varies with h a . ● According to Newton’s law of gravity, g = g o [R/h a ] 2 = g o [R/(R + h G ) ] 2 where g o is g at sea-level where 3-Geopotential Altitude h is a fictitious (hypothetical) altitude used to facilitate the calculations ( h ≠ h G )

7. h a R h G Surface of earth ( Sea level) Definition of altitude By definition : dp = - ρ g dh G = - ρ g o dh Then : dh/dh G = g / g o

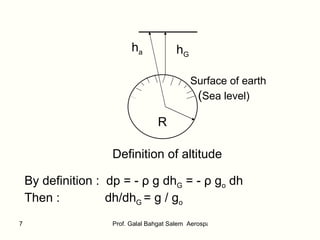
8. What is the relation between h & h G ? dh = R 2 /(R+h G ) 2 dh G Integrate: 0 ∫ h dh = 0 ∫ h G R 2 /(R+h G ) 2 dh G The result is: h = [R/(R+h G )] h G At h G = 6.5 km , h is less than h G by about 0.1% only. At h G = 65 km , h is less than h G by about 1% only. The Standard Atmosphere (SA) It is defined in order to relate flight tests, wind-tunnel tests, and the general design and performance of flying vehicle ( aircraft, missile, satellite,….etc ) to a common reference.

9. It gives mean values of p, T, ρ , and other properties as function of altitude. These values are obtained from experimental balloons and sounding-rocket measurements with a mathematical model of the atmosphere ( based on the equation of state and the hydrostatic equation). Several different standard atmospheres exist, due to using different experimental data in the models, but the differences are insignificant below 30 km (100,000 ft), which is the domain of contemporary airplanes. ■ Definition Of The Standard Atmosphere (SA) ● The standard atmosphere (SA) is defined by: 1. Conditions at sea-level:

10. p o = 1.01325 x 10 5 N/m 2 = 2116.2 Ib/ft 2 T o = 288.16 o K = 518.60 o R ρ o = 1.225 kg/m 2 = 0.002377 slug/ft 2 g o = 9.807 m/s 2 = 32.17 ft/s 2 2. A defined variation of T with altitude, based on experimental evidence, as shown in Figure. # Given T = T(h), then p = p(h) and ρ = ρ (h) can now be determined by calculation. # The atmospheric layers of the SA are either isothermal or gradient layers, as shown in Figure.

11. Temperature distribution in the standard atmosphere

12. Atmospheric properties variation of SA

13. (A) Calculation in an Isothermal Layer: h 1 h T,p, ρ T 1 ,p 1 , ρ 1 Isothermal Layer Base of Isothermal Layer From the hydrostatic equation: dp = - ρ g o dh Substitute ρ from the equation of state : p = ρ RT dp/p = - (g o /RT) dh (1)

14. Integrate: p 1 ∫ p dp/p = -(g o /RT) h 1 ∫ h dh Hence, ln (p/p 1 ) = -(g o /RT) (h – h 1 ) Or : (p/p 1 ) = e -(g o /RT)(h – h 1 ) = ( ρ / ρ 1 ) (2) Because , ( p/p 1 ) = ( ρ T/ ρ 1 T 1 ) = ( ρ / ρ 1 ) from equation of state and T = T 1 (3)

15. (B) Calculation in a Gradient Layer: h T,p, ρ Base of layer h 1 T 1 ,p 1 , ρ 1 The temperature variation is linear, (T-T 1 )/(h-h 1 ) = dT/dh = a a is the temperature lapse rate ( +ve or –ve) T = T 1 + a (h – h 1 ) (4) Then, dh = dT/a and substitute into Eqn.(1) dp/p = - (g o /aR) dT/T

16. Integrate: p1 ∫ p dp/p = -(g o /aR) T1 ∫ T dT/T Hence, ln p/p 1 = - (g o /aR) ln T/T 1 Then, p/p 1 = (T/T 1 ) -g o /aR (5) From equation of state: ( p/p 1 ) = ( ρ T/ ρ 1 T 1 ) = ( ρ / ρ 1 )(T/T1) Hence, ( ρ / ρ 1 ) = (T/T1) -[(g o /aR)+1] (6) Where T is calculated from Eq.(4)

17. With the Figure of variation of T with h and Eqs.(2),(3),(4),(5), and (6) a Table of values for the Standard Atmosphere is constructed and is given in Appendix A for SI units and Appendix B for English Engineering Units (see textbook “Introduction to Flight”, Anderson, pages 709-729) 4.Pressure Altitude h p : The altitude in the Standard Atmosphere corresponding to a particular static air pressure. 5 .Temperature Altitude h T : The altitude in the Standard Atmosphere corresponding to a particular air temperature. 6.Density Altitude h ρ : The altitude in the Standard Atmosphere corresponding to a particular air density.