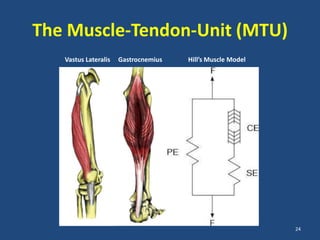
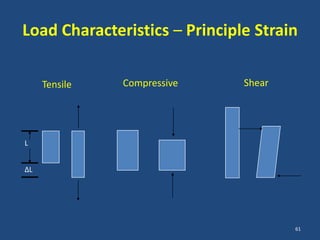
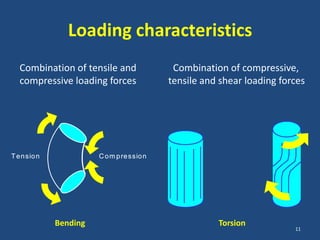
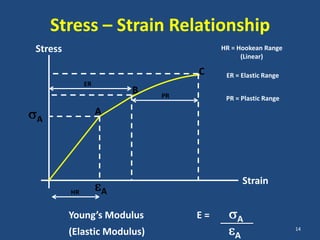
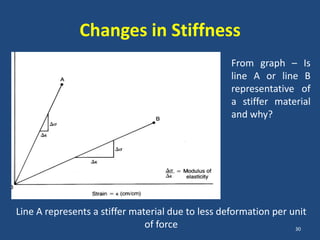
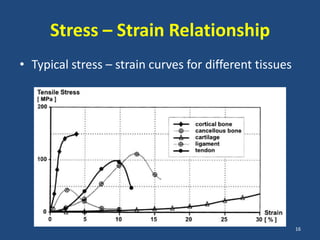
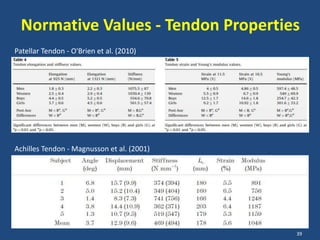
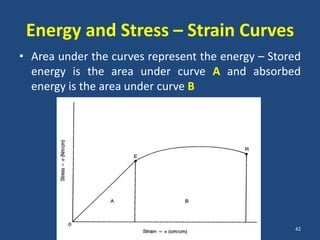
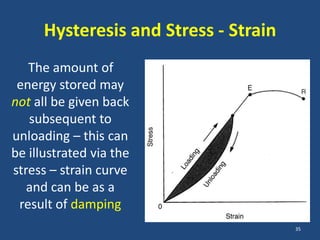
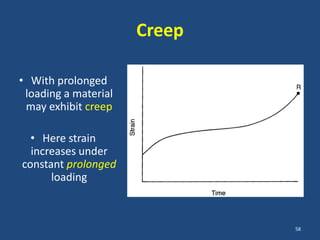
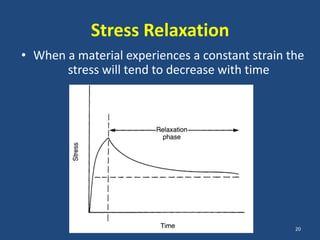
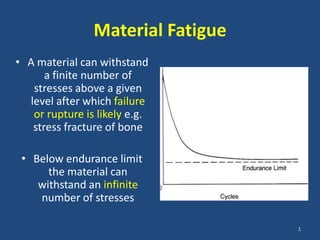
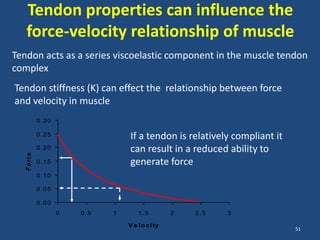
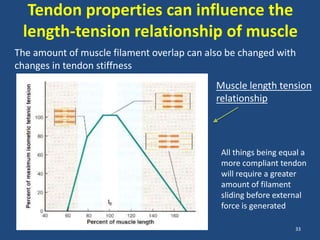
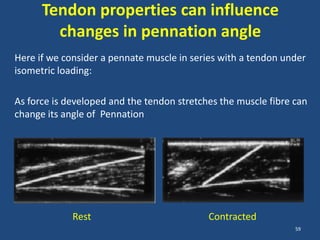
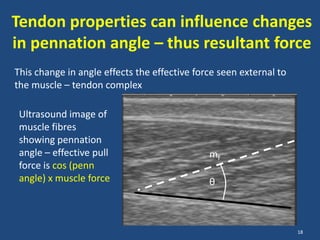
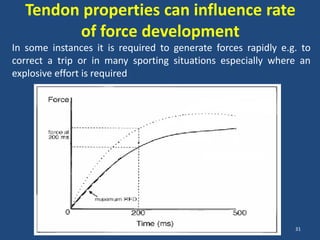
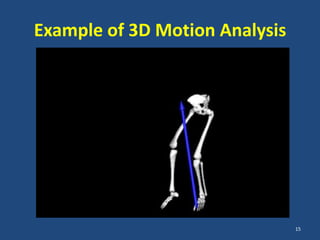
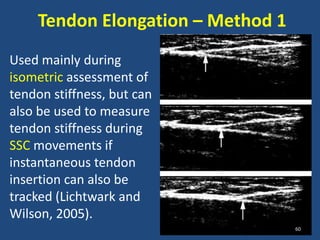
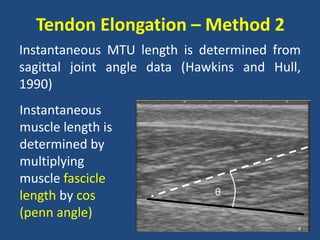
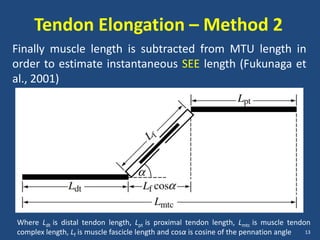
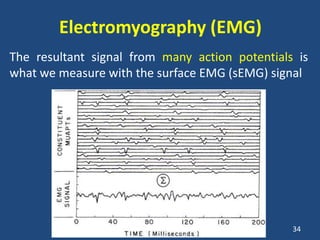
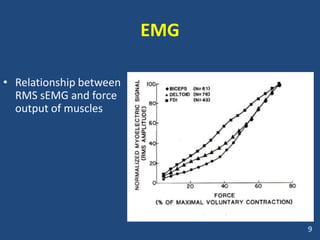
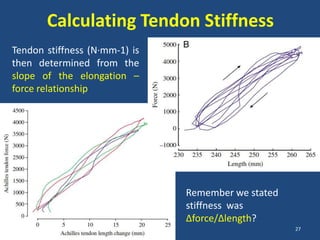
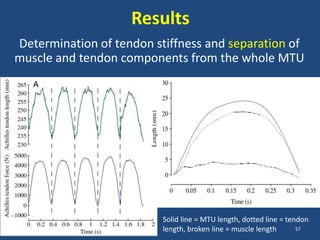
The document covers the mechanical concepts related to tendon mechanics, including strain, stress, and the rheological properties of materials. It discusses the influence of tendon mechanical properties on muscle function, including their effects on force-velocity and length-tension relationships. Finally, it outlines the impact of training, stretching, and in vivo measurement techniques on tendon properties.

1. Tendon Mechanics
Biomechanics for Sport III
John McMahon BSc (Hons), ASCC, CSCS

2. Lecture Aims
• To remind you of the mechanical concepts of
strain, stiffness and compliance
• To examine the rheological properties of
materials & illustrate mechanical responses to
loading
• To discuss the influence of tendon mechanical
properties on muscle function
• To introduce the affect of stretching & training on
tendon mechanical properties
• To understand in vivo measurement of tendon
stiffness during dynamic exercises
32

3. The Muscle-Tendon-Unit (MTU)
Vastus Lateralis Gastrocnemius Hill’s Muscle Model
24

4. Strain
• The loading of a material will cause a deformation, which is
known as strain
• There are 3 main types of load and therefore strain:
• Tension = pulling force - makes object longer and thinner
• Compression = pushing force - makes object shorter and
thicker
• Shear = a load comprised of 2 equal, opposite and parallel
forces that tend to displace one part of an object with
respect to an adjacent part along a plane parallel and
between the line of the forces 47

5. Load Characteristics – Principle Strain
Tensile Compressive Shear
L
∆L
61

6. Loading characteristics
Combination of tensile and Combination of compressive,
compressive loading forces tensile and shear loading forces
T e n sio n C o m p re ssio n
Bending Torsion
11

7. Calculating Strain
• If the loading is longitudinal i.e. in tension the material
will tend to elongate
• The strain can be defined as change in length/original
length
• Strain, = Change in length r
Original length r
• This is unit less i.e. cm/cm and is usually expressed as a
percentage - Strain = ∆L/L *100
7

8. Stress
• When a material undergoes a deformation as a result of
applied forces it reacts to this change
Stress:
= the resistance of the intermolecular bonds of an object to
the strain caused by a load
= the measure of a material’s ability to resist an applied force
• Can be defined as “the internal force per unit area upon a
cross section of that a part of a body”
Stress, = Force F (Pa)
Cross-Sectional Area A
• Stress can be longitudinal (normal) or transverse to the
cross section
28

9. Rheological Properties of Materials
Rheology - the study of the deformation and flow of matter
• Elasticity – relates to the ability of the material to return to
its original dimension after loading – for a purely elastic
material the relationship between loading and deformation
will be a straight line – i.e. energy is stored
• Viscosity – here the material will deform with loading but
will have a lag between developing stress and the resultant
strain – the greater the rate of loading, the greater the
stress developed – the material will retain its new
shape/size – i.e. energy is absorbed
49

10. Rheological Properties of Materials
• Material can possess properties of both viscosity
and elasticity and hence be viscoelastic. Here the
material will tend to deform and return to its
original shape in a non linear fashion
• Plasticity – here when the material is deformed it
tends to retain its new shape/size. Deformation
tends to be without a lag and energy is absorbed
56

11. Stress – Strain Relationship
Stress HR = Hookean Range
(Linear)
C ER = Elastic Range
ER
B PR PR = Plastic Range
A
A
Strain
HR A
Young’s Modulus E= A
14
(Elastic Modulus) A

12. Stress – Strain Relationship
(Stiffness and Compliance)
• It allows the description of the material in terms of the
rheological properties previously defined
• It relates to Hooke’s law and allows the determination of
the material ‘stiffness’ – Young’s modulus (E = ∆σ/∆ε)
• A very stiff material can tolerate high loads (stress) with
only small deformations (strain)
• A higher value for E is indicative of a stiffer material
• Compliance is sometimes used instead of stiffness and is
simply the inverse of stiffness i.e. the ratio of strain change
to stress change 52

13. Changes in Stiffness
From graph – Is
line A or line B
representative of
a stiffer material
and why?
Line A represents a stiffer material due to less deformation per unit
of force 30

14. Stress – Strain Relationship
• Typical stress – strain curves for different tissues
16

15. Normative Values - Tendon Properties
Patellar Tendon - O'Brien et al. (2010)
Achilles Tendon - Magnusson et al. (2001)
39

16. Energy and Stress – Strain Curves
• Area under the curves represent the energy – Stored
energy is the area under curve A and absorbed
energy is the area under curve B
42

17. Hysteresis and Stress - Strain
The amount of
energy stored may
not all be given back
subsequent to
unloading – this can
be illustrated via the
stress – strain curve
and can be as a
result of damping
35

18. Creep
• With prolonged
loading a material
may exhibit creep
• Here strain
increases under
constant prolonged
loading
58

19. Stress Relaxation
• When a material experiences a constant strain the
stress will tend to decrease with time
20

20. Material Fatigue
• A material can withstand
a finite number of
stresses above a given
level after which failure
or rupture is likely e.g.
stress fracture of bone
• Below endurance limit
the material can
withstand an infinite
number of stresses
1

21. Tendon Injury
Research performed using isolated tendons:
For Achilles tendon:
• Maximum Modulus: 819 MPa
• Failure Load: 5098 N
• Failure Stress: 79 MPa (Wren et al., 2001)
Damage may occur at:
• 15-30% strain (Haut & Pawlinson, 1990;
Stäubli et al., 1999)
43

22. Tendon Injury
However, in vivo tendon research has shown:
• Tendon strains of 6-14% during MVC and up to
11.4% during SSC without injury occurrence
• Tendon forces to reach in excess of 5000 N
Differences due to:
• Preservatives
• Tendon tested
• Region of tendon tested
22

23. Factors Affecting Mechanical
Properties of Tendon
• Age
• Gender
• Stretching
• Training
• Fatigue
• Chronic disease
• Time of day
3

24. Influence of Tendon Mechanical
Properties on Muscle Function
37

25. Why study tendon mechanical
properties?
Function of tendons:
• Tensile force transmission
• Storage and release of energy during locomotion
(Maganaris and Paul, 2002)
The mechanical properties of tendon significantly affect muscle
output and function
25

26. Tendon properties can influence the
force-velocity relationship of muscle
Tendon acts as a series viscoelastic component in the muscle tendon
complex
Tendon stiffness (K) can effect the relationship between force
and velocity in muscle
0.30
0.25 If a tendon is relatively compliant it
0.20 can result in a reduced ability to
F o rce
0.15 generate force
0.10
0.05
0.00
0 0.5 1 1.5 2 2.5 3
V e l o c i ty
51

27. Tendon properties can influence the
length-tension relationship of muscle
The amount of muscle filament overlap can also be changed with
changes in tendon stiffness
Muscle length tension
relationship
All things being equal a
more compliant tendon
will require a greater
amount of filament
sliding before external
force is generated
33

28. Tendon properties can influence
changes in pennation angle
Here if we consider a pennate muscle in series with a tendon under
isometric loading:
As force is developed and the tendon stretches the muscle fibre can
change its angle of Pennation
Rest Contracted
59

29. Tendon properties can influence changes
in pennation angle – thus resultant force
This change in angle effects the effective force seen external to
the muscle – tendon complex
Ultrasound image of
muscle fibres
showing pennation
angle – effective pull mf
force is cos (penn
angle) x muscle force θ
18

30. Tendon properties can influence rate
of force development
In some instances it is required to generate forces rapidly e.g. to
correct a trip or in many sporting situations especially where an
explosive effort is required
Low K
High K
31

31. RFD - EMD
This also has an effect on electro mechanical delay (the time lag
between muscle activation and muscle force production)
This could effect the ability to carry out a number of motor tasks
due to the delay between muscle activation and external movement
Compliant tendons would delay action of muscle spindles (stretch
reflex)
26

32. Energy storage and release - SSC
Movement economy can also be modulated as energy is capable
of being stored and released from the tendon
Stretch-shorten-cycle (SSC)
Activation of muscle during
lengthening of muscle –
increased lengthening of
tendon
Energy stored in tendon
and released during From Kawakami
concentric contraction – et al. J. Physiol.
up to ~93% of energy is (2002)
returned (Alexander, 2000) 40

33. Affect of Stretching and Training on
Tendon Mechanical Properties
5

34. Passive Stretching
Acute:
• 10 min calf stretch - ↓ K & Hysteresis (Kubo et al., 2001a)
• 5 min calf stretch - ↓ K & Young’s Modulus (Burgess et al., 2009)
- greater decreases in female subjects
• 5 min calf stretch - ↓ K & Hysteresis (Kubo et al., 2002b)
Changes above due to ↓ Viscosity & ↑ Elasticity
Chronic:
• 5 x 45s (15s rest) calf stretch 2 x day for 3 weeks:
↔ K & ↓ Hysteresis (Kubo et al., 2002a)
8

35. Isotonic Resistance Training
6 weeks of:
• ‘Eccentric’ heel drops (BW): ↔ K (Mahieu et al., 2008)
8 weeks of:
• Calf raises (70% 1RM):↑ K & ↔ Hysteresis (Kubo et al., 2002c)
12 weeks of:
• Leg extension (70% 1RM): ↑ K (Kongsgaard et al., 2007)
14 weeks of:
• Leg extension/leg press (80% 1RM): ↑ K (Reeves et al., 2003a,b)
6 months of:
• BW squat: ↔ K (Kubo et al., 2003) 38

36. Isometric Resistance Training
12 weeks of isometric knee extension performed at
70% MVC for 15-20s:
• ↑ K (Kubo et al., 2001c,d; 2006; 2009)
• ↑ muscle size and RFD (Kubo et al., 2001d)
↔ K during above exercise when:
- Performed for short duration (1s)
- Performed at short muscle length (50 deg)
- Performed for < 8 weeks
45

37. Isometric Resistance Training
14 weeks of isometric plantar flexion performed
at 90% MVC for 3s:
• ↑ K (Arampatzis et al., 2007; 2010)
Authors concluded that the strain magnitude
during isometric training should exceed the
value experienced during habitual loading for
mechanical adaptations in tendon to occur.
62

38. Plyometric Training
14 weeks of plyometric training (SJ, CMJ, DJ
(40+60+80), over barrier)
• ↑ K (Fouré et al., 2010)
Trained with high volume: 36 sessions in total
consisting of 200-600 jumps per session
10

39. Combination Training
6 weeks of Plyometric (DJ) vs Isometric (Plantar):
• Plyo: ↑ K (29%), ↑ RFD (19%) & ↑ SJ height (59%)
• Iso: ↑ K (62%), ↑ RFD (17%) & ↑ SJ height (64%)
(Burgess et al., 2007)
12 weeks of Iso RT (80% 1RM calf raise) vs Plyo (sledge
hopping & DJ (20)):
• Iso RT: ↑ K, ↑ SJ height
• Plyo: ↔ K, ↑ SJ, CMJ & DJ height
(Kubo et al., 2007)
19

40. Endurance Training
• No effect of endurance training on mechanical
properties (i.e. K/Young’s Modulus) of the PT or AT
(Rosager et al., 2002; Hansen et al., 2003;
Karamanidis and Arampatzis, 2006; Arampatzis et
al., 2007)
46

41. Training Summary
For necessary adaptations of tendon mechanical
properties to occur, training should:
• Include high loads
• Involve high tendon strains
• If isometric, be performed at long muscle lengths
• If isometric, be performed for at least 3s/rep
• Be performed consistently for at least 6-8 weeks
21

42. Measurement of Tendon Mechanical
Properties (in vivo) during Dynamic
Movements
12

43. Measurement of Tendon Properties
In order to estimate tendon mechanical properties
(stiffness) both elongation and force in the tendon
have to be determined
In order to measure the mechanical properties of
tendon in vivo we use a combination of:
• Motion Analysis
• Ultrasonography
• Electromyography
• Dynamometry
• Force
36

44. Motion Analysis – Sagittal Plane
• Can use 2D or 3D motion capture depending on
information required for research
• Markers placed on lateral aspects of ankle, knee
and hip joints (marker on tendon insertion may
also be necessary)
• Sagittal motion of the above joints required to
calculate instantaneous MTU length and tendon
moment arms using regression equations
obtained from cadaver studies (Hawkins and Hull,
1990; Visser et al., 1990)
44

45. Example of 3D Motion Analysis
15

46. Ultrasound – Mode of Operation
• B-mode ultrasound is a useful tool for the
imaging of soft tissue.
• Its mode of operation is via the transmission and
reception of sound waves.
• Ultrasound waves are produced by oscillating
crystals at a frequency that is inaudible to the
human ear.
• Transducers located in the probe produce sound
(for example) at 7.5mhz which is then pulsed at
intervals which occur every 20 micro-seconds.
2

47. Ultrasound – Mode of Operation
• These sound waves penetrate and encounter the
different tissue interfaces as they travels through
the body.
• When sound encounters tissues or tissue planes,
part of the wave is reflected back to receivers in
this same probe.
• The transducer must be in contact with the
medium scanned, in this case skin, so a
"transmission jelly" is used to insure a complete
"union". The ultrasound produced can not travel
through the air and then into the body.
23

48. Ultrasound – Mode of Operation
• This mode analyses the intensity of the returning
ultrasound signal as well as the direction and depth
from, which it was reflected
• A two-dimensional grey-scale image is constructed
with different intensities from the returning signals
being assigned different levels of brightness
• Generally, a high-density structure such as
tendon/bone will reflect a high-intensity signal back to
the probe and be displayed as white on the screen
• We use ultrasonography to measure tendon elongation
53

49. Tendon Elongation – Method 1
Used mainly during
isometric assessment of
tendon stiffness, but can
also be used to measure
tendon stiffness during
SSC movements if
instantaneous tendon
insertion can also be
tracked (Lichtwark and
Wilson, 2005).
60

50. Tendon Elongation – Method 2
Instantaneous MTU length is determined from
sagittal joint angle data (Hawkins and Hull,
1990)
Instantaneous
muscle length is
determined by
multiplying
muscle fascicle
length by cos θ
(penn angle)
4

51. Tendon Elongation – Method 2
Finally muscle length is subtracted from MTU length in
order to estimate instantaneous SEE length (Fukunaga et
al., 2001)
Where Ldt is distal tendon length, Lpt is proximal tendon length, Lmtc is muscle tendon
complex length, Lf is muscle fascicle length and cosα is cosine of the pennation angle 13

52. Electromyography (EMG)
The resultant signal from many action potentials is
what we measure with the surface EMG (sEMG) signal
34

53. EMG
• sEMG allows the determination of when a muscle
is switched on or off
• The root mean square (RMS) value of a sEMG
signal has been suggested to be a measure of the
strength of muscle activity
• For some muscles it has been shown that there is
essentially a linear relationship between sEMG
RMS and force output (Lippold, 1952)
41

54. EMG
• Relationship between
RMS sEMG and force
output of muscles
9

55. EMG
How do we measure this electrical activity?
• For simple single differential measurement (to
reduce noise) 2 electrodes are placed over the
muscle belly of interest
• The signal is then
amplified and
filtered before
being sampled by
a computer to be
saved
17

56. EMG’s use in
determining tendon properties
• To determine levels of co-contraction and
hence co-contraction force.
• During agonist muscle contraction antagonists
are also active and producing force.
• The agonists must overcome this ‘hidden’
force before external torque is recorded
through force readings.
44

57. Dynamometry
• Used to determine EMG activity of agonist and antagonist
muscles during MVC – used to calculate antagonist force
Co-contraction effort (CT) defined as:
(EMG during extension / Max flexor EMG)*Max flexor torque
Total extensor torque = CT + Extensor torque
• Allows EMG activity attained during dynamic movement to
be normalised to EMG activity attained during MVC (when
comparing groups)
• Can be assessed over a range of joint angles specific to the
range demonstrated during the dynamic task 38

58. Ground Reaction Force Data
Required to calculate tendon forces
Tendon force is derived
by multiplying
instantaneous joint
moment (as determined
using inverse dynamics)
by instantaneous
tendon moment arm
(Visser et al., 1990)
50

59. Calculating Tendon Stiffness
Tendon stiffness (N·mm-1) is
then determined from the
slope of the elongation –
force relationship
Remember we stated
stiffness was
∆force/∆length?
27

60. Results
Determination of tendon stiffness and separation of
muscle and tendon components from the whole MTU
Solid line = MTU length, dotted line = tendon
length, broken line = muscle length 57

61. Normalizing Values
• Differences in tendon length and/or cross
sectional area can affect the stiffness values
• It is therefore important to normalise the
stiffness to account for these dimensional
factors when comparing different groups
Young's modulus is such a value:
K*(L/CSA) or stress/strain
29

62. Any Questions?
54