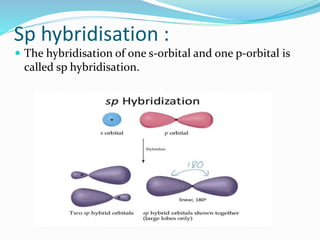
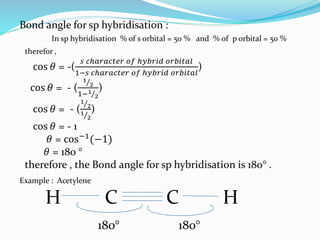
The document presents a seminar topic on hybridization given by Tarkesh D. Diwate, which discusses the concepts of sp, sp2, and sp3 hybridization including the properties of hybrid orbitals, shapes of atomic orbitals, types of hybridization, and examples such as ethylene and acetylene. Key aspects covered include how hybrid orbitals are formed by mixing atomic orbitals of similar energies, their orientations and equal energies, and how hybridization explains molecular geometry and bonding properties.




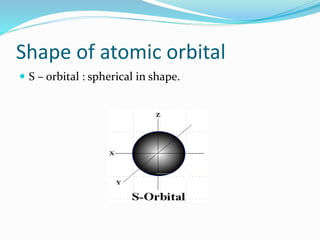
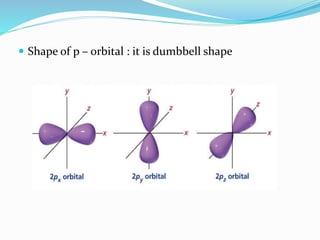
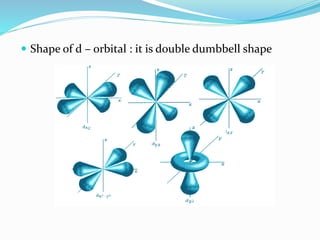

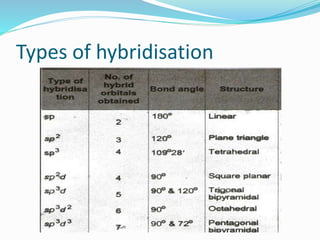









![Tarkesh 2nd sem[1]](https://image.slidesharecdn.com/tarkesh2ndsem1-181012124601/85/Tarkesh-2nd-sem-1-21-320.jpg)