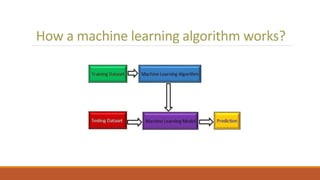
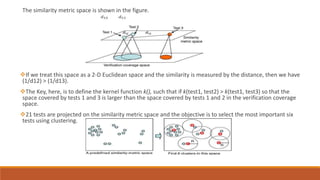
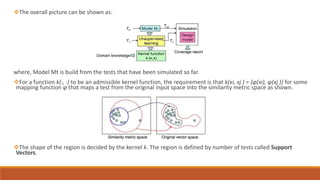
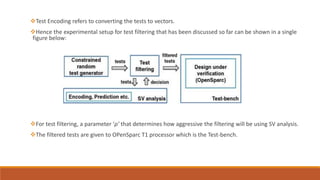
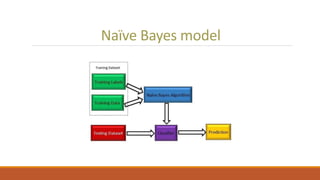
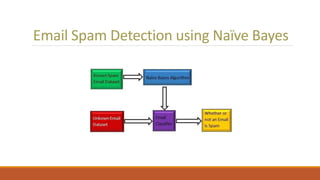
This document discusses using unsupervised support vector analysis to increase the efficiency of simulation-based functional verification. It describes applying an unsupervised machine learning technique called support vector analysis to filter redundant tests from a set of verification tests. By clustering similar tests into regions of a similarity metric space, it aims to select the most important tests to verify a design while removing redundant tests, improving verification efficiency. The approach trains an unsupervised support vector model on an initial set of simulated tests and uses it to filter future tests by comparing them to support vectors that define regions in the similarity space.

1. Increasing the Efficiency of Simulation-Based
Functional Verification through Unsupervised
Support Vector Analysis
Onur Guzey, Li-C. Wang, Jeremy R. Levitt, and HarryFoster
01/15/2018
SAI KIRAN KADAM

2. Machine learning?
Machine learning (ML) is a data analysis method that is used to create an analytical model base
on a set of data.
That analytic model has the ability to learn without being explicitly programmed as new data is
being fed to it.
ML has been around for quite some time, but only recently has it proved to be useful due to
the following:
The growing volumes and varieties of available data from social media and on the Internet are
increasingly available.
Computer systems (hardware) are getting more powerful.
Data storages are getting larger and cheaper.
The two most common types of ML are supervised learning and unsupervised learning.

3. Deep learning!

4. Supervised vs Unsupervised learning
Supervised Learning:
Algorithms are trained using a set of input data and a set of labels (known results.)
Each time algorithms learn by comparing the results of the input data with the label and adjust
the machine learning model.
Classification is considered supervised learning.
Un-Supervised Learning:
Algorithms have no labels to learn from.
Instead, they have to look through input data and detect patterns on their own.
For example, to categorize which region in the world a person belongs to, the algorithms have
to look at the population data, identify races, religions, languages, and so on.

5. How a machine learning algorithm works?

6. Support Vector Machines
“Support Vector Machine” (SVM) is a supervised machine learning algorithm mostly
used in classification problems.
Each data item is plotted as a point in n-dimensional space with the
value of each feature being the value of a particular coordinate.
Classification is performed by finding the hyper-plane that differentiates
separating the two classes very well.
Here, kernel based Unsupervised Support Vector analysis has been used to filter the redundant tests
while performing simulation based functional verification
A kernel can be defined as a function k() that measures the similarity between a pair of tests (similarity
metric space) which, eventually, may be used to filter redundant tests.

7. The similarity metric space is shown in the figure.
If we treat this space as a 2-D Euclidean space and the similarity is measured by the distance, then we have
(1/d12) > (1/d13).
The Key, here, is to define the kernel function k(), such that if k(test1, test2) > k(test1, test3) so that the
space covered by tests 1 and 3 is larger than the space covered by tests 1 and 2 in the verification coverage
space.
21 tests are projected on the similarity metric space and the objective is to select the most important six
tests using clustering.

8. The overall picture can be shown as:
where, Model Mt is build from the tests that have been simulated so far.
For a function k(·, ·) to be an admissible kernel function, the requirement is that k(xi, xj ) = {φ(xi), φ(xj )} for some
mapping function φ that maps a test from the original input space into the similarity metric space as shown.
The shape of the region is decided by the kernel k. The region is defined by number of tests called Support
Vectors.

9. Equations used:
Where R= radius of the hyper sphere.
α α k(x⃗ , x⃗ ) – 2. α k(x⃗ , x⃗) + k(x⃗, x⃗) = weighted average of distance squares between x⃗ and all SVs, α
deciding all the weights.
Hence, nonsupport vectors are not used in this model. S(x⃗) ≥ 0 means that x⃗ is inside the region.
Otherwise, it is outside.
Commonly used Kernels:
1. Dot Product Kernel:
2. Polynomial Kernel:
where ‘d’ is the degree of the polynomial
and Gaussian Kernel:
Where g is a parameter that decides the Gaussian width that scales the similarity measure.

10. Test Encoding refers to converting the tests to vectors.
Hence the experimental setup for test filtering that has been discussed so far can be shown in a single
figure below:
For test filtering, a parameter ‘ρ’ that determines how aggressive the filtering will be using SV analysis.
The filtered tests are given to OPenSparc T1 processor which is the Test-bench.

11. Different Learning Algorithms
Linear Regression
Logistic Regression
Decision Tree
Support Vector Machine
Naïve Bayes
KNN (K-Nearest Neighbors)
Random forest
Gradient boosting and ADA boost
Dimensionality reduction algorithm

12. Naïve Bayes model
A Naive Bayes classifier assumes that the presence of a particular feature in a class is unrelated
to the presence of any other feature.
Even if these features are related to each other, a Naive Bayes classifier would consider all of
these properties independently when calculating the probability of a particular outcome.
A Naive Bayesian model is easy to build and useful for massive datasets. It's simple, and is
known to outperform even highly sophisticated classification methods

13. Naïve Bayes model

14. Email Spam Detection using Naïve Bayes

15. Bayes Theorem:
Let X be the data record (case) whose class label is unknown. Let H be some hypothesis, such
as data record X belongs to a specified class C. For classification, we want to determine P (H|X) --
the probability that the hypothesis H holds, given the observed data record X.
P (H|X) is the posterior probability of H conditioned on X. For example, the probability that a
fruit is an apple, given the condition that it is red and round. In contrast, P(H) is the prior
probability of H. In this example P(H) is the probability that any given data record is an apple,
regardless of how the data record looks.
Similarly, P (X|H) is posterior probability of X conditioned on H. That is, it is the probability that
X is red and round given that we know that it is true that X is an apple. P(X) is the prior
probability of X, i.e., it is the probability that a data record from our set of fruits is red and
round. Bayes theorem is useful in that it provides a way of calculating the posterior probability,
P(H|X), from P(H), P(X), and P(X|H). Bayes theorem is,
P (H|X) = P(X|H) P(H) / P(X)

16. Pros and Cons!
Unlike SVM’s a Naive Bayesian model is easy to build and useful for massive datasets.
It's simple, and is known to outperform even highly sophisticated classification methods.
It is known for its high speed operation.
NB does well with multi-class prediction.
oIf the data has no label in the training data set, NB cannot make a prediction.
oFeatures/events are not always completely independent.
oIt takes a considerable amount of time to train the model with a large data set. It can take
weeks and even months to train a particular model.

17. SVM vs Naïve Bayes!
There is no single answer about which is the best classification method for a given dataset.
Different kinds of classifiers should be always considered for a comparative study over a given
dataset. Given the properties of the dataset, you might have some clues that may give
preference to some methods. However, it would still be advisable to experiment with all, if
possible.
Naive Bayes Classifier (NBC) and Support Vector Machine (SVM) have different options
including the choice of kernel function for each. They are both sensitive to parameter
optimization (i.e. different parameter selection can significantly change their output) . So, if
you have a result showing that NBC is performing better than SVM. This is only true for the
selected parameters. However, for another parameter selection, you might find SVM is
performing better.
In summary, we should not prefer any classification method if it outperforms others in one
context since it might fail severely in another one.