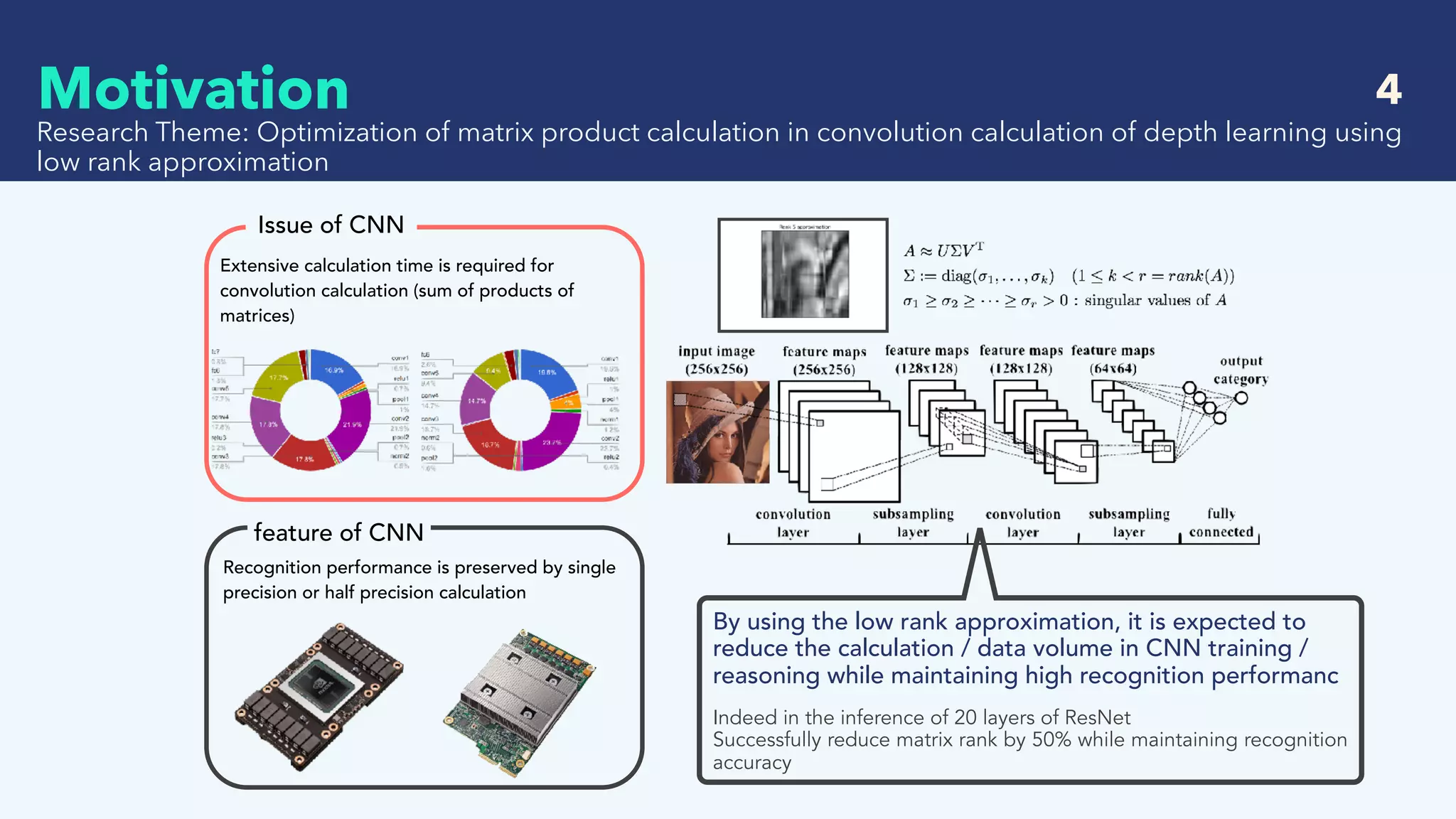
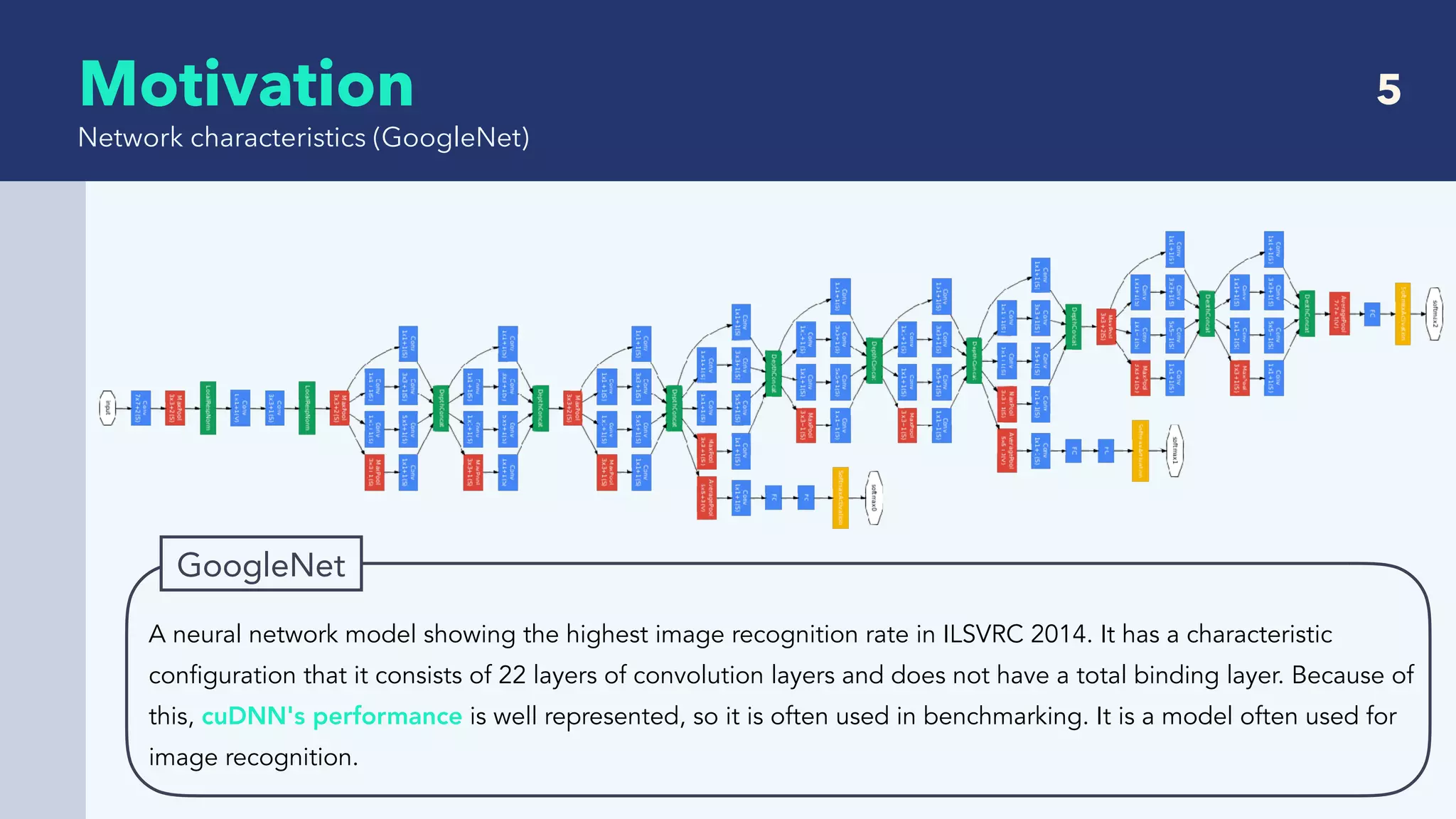
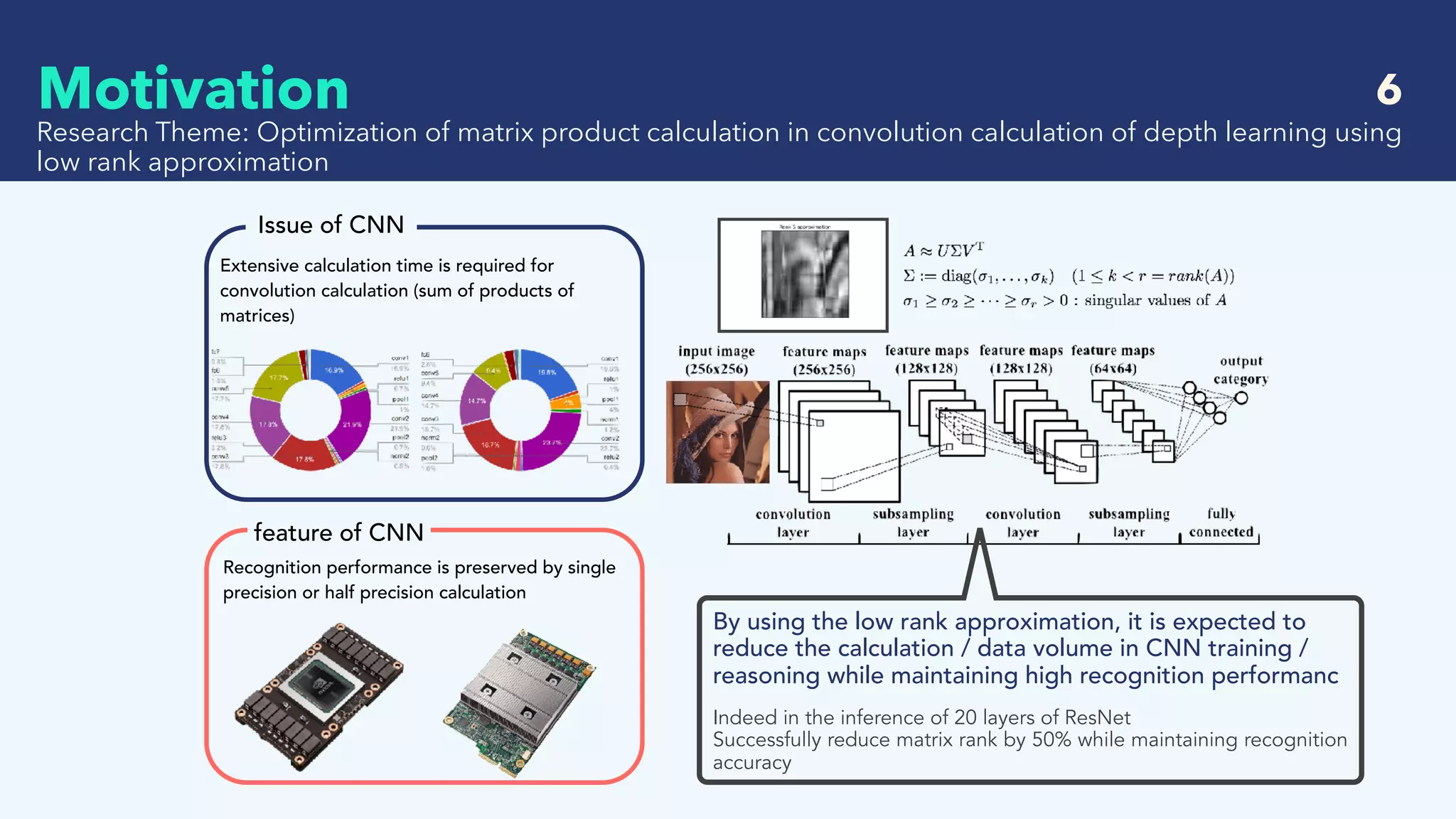
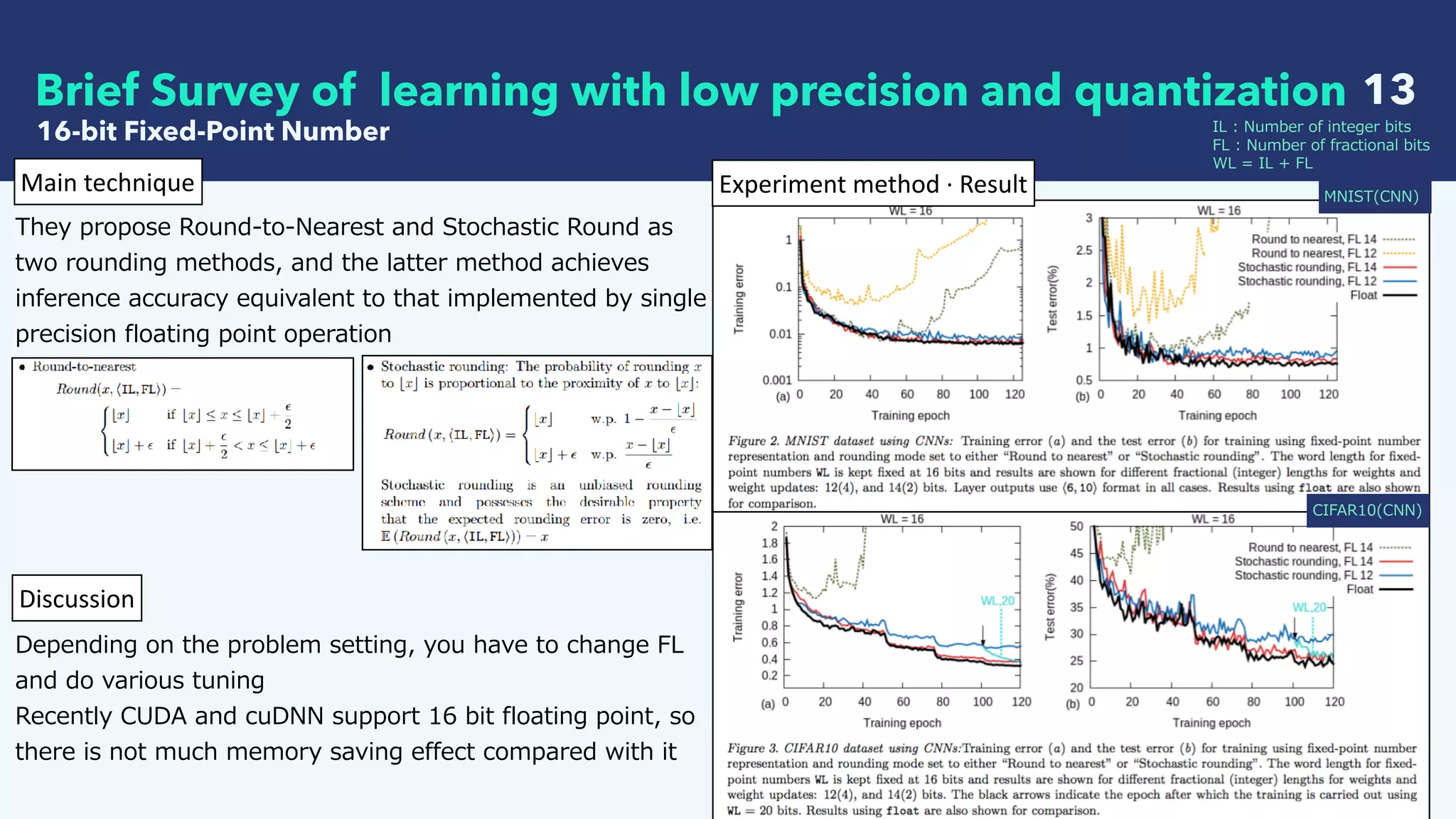
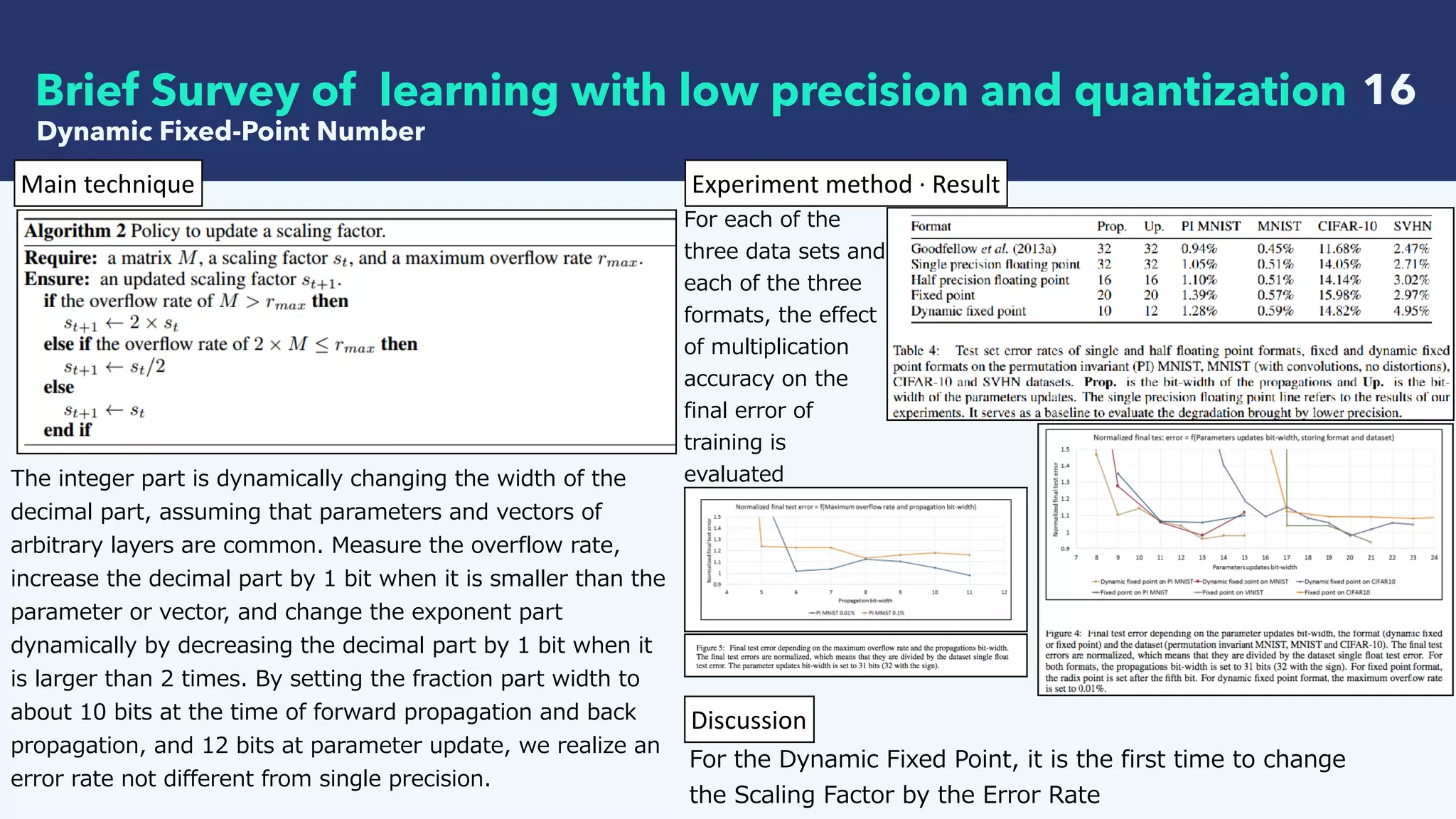
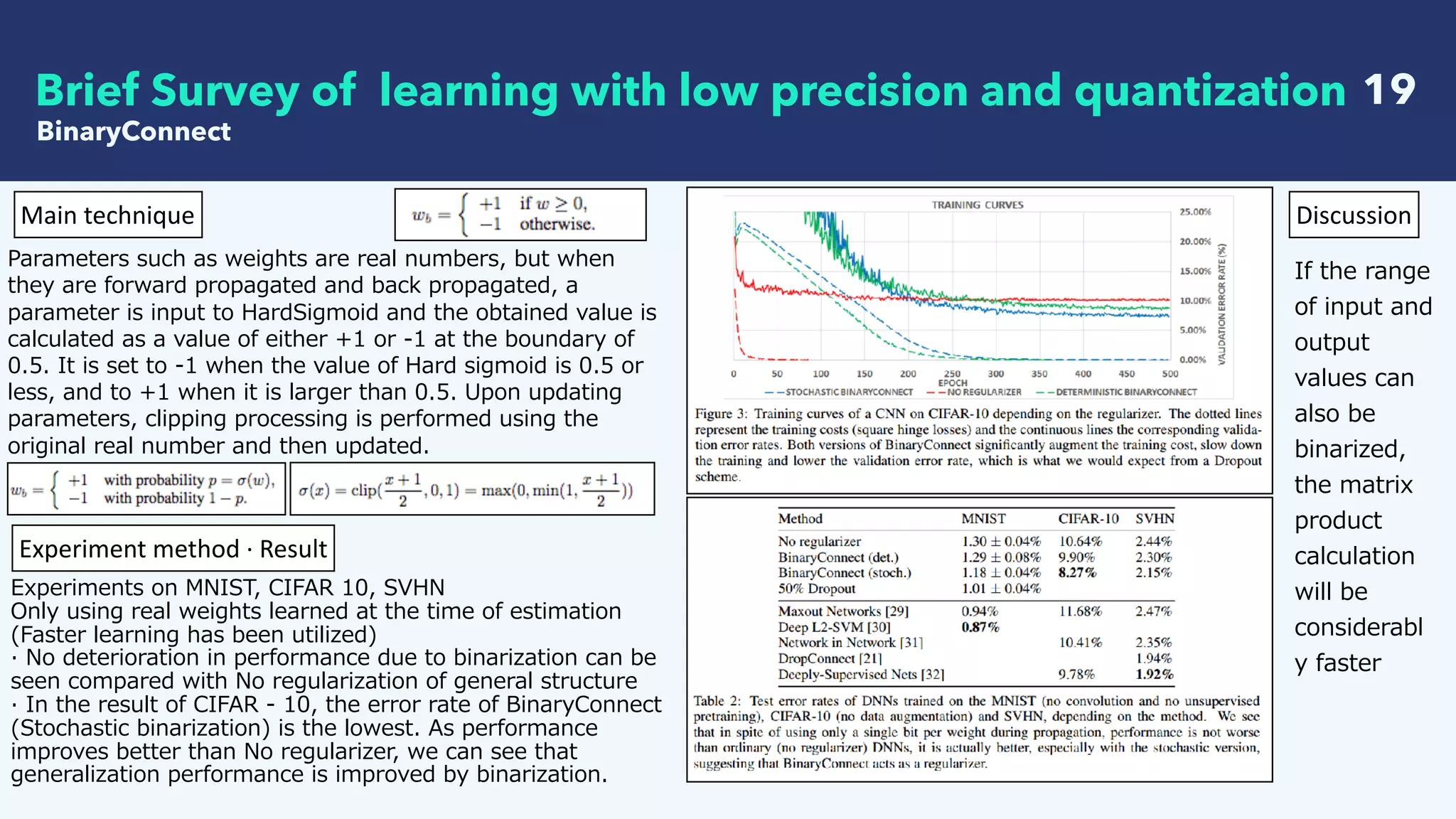
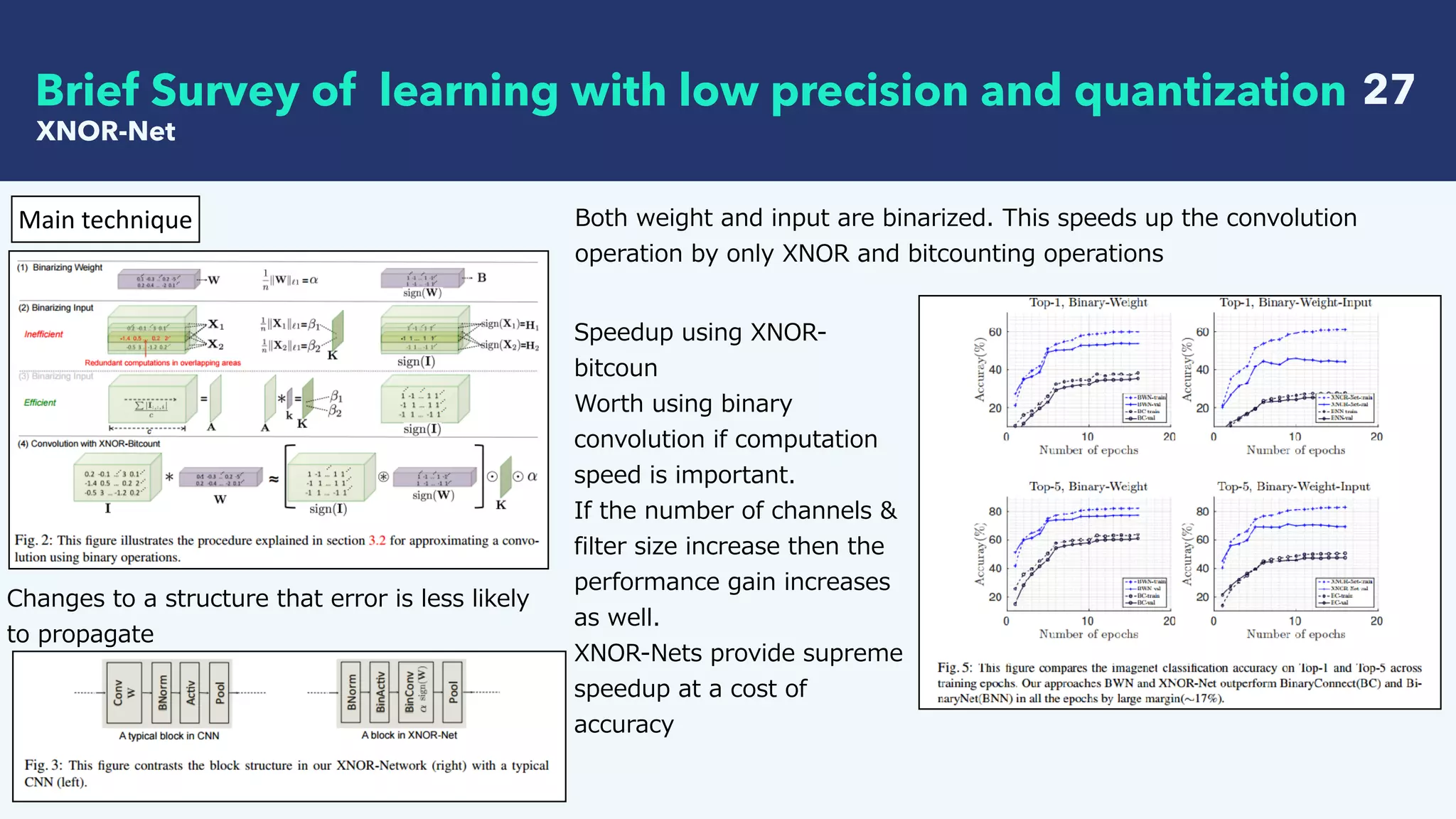
This document summarizes recent research on deep learning with low precision numerical representations. It discusses 6 different methods for reducing precision: 16-bit fixed-point, dynamic fixed-point, 8-bit approximate representation, BinaryConnect, BinaryNet, and XNOR-Nets. For each method, it provides an abstract, the key techniques used, experimental results on datasets like MNIST and CIFAR-10, and a discussion of findings. The overall goal of these methods is to reduce computational and memory costs while maintaining high recognition performance in neural networks.

1.
Survey of recent deep learning
with low precision
Tokyo Institute of Technology School of Computing
Department of Computer Science
Yokota Rio Group
Master’s 1st Year
Hiroki Naganuma
Meeting 11.July.2017

2.
Outline 2
→ Why do you want to quantize the neural network and reduce computational accuracy?
Motivation
→ I introduce 6 methods on numerical precision of parameters
Brief Survey of learning with low precision and quantization
→ based on “CONVNET TRAINING WITH HALF-FLOAT PRECISION” @GTC 2017
Survey NV-caffe-0.16 (16-bit Floating-Point)

3.
Outline 3
→ Why do you want to quantize the neural network and reduce computational accuracy?
Motivation
→ I introduce 6 methods on numerical precision of parameters
Brief Survey of learning with low precision and quantization
→ based on “CONVNET TRAINING WITH HALF-FLOAT PRECISION” @GTC 2017
Survey NV-caffe-0.16 (16-bit Floating-Point)

4. 4
Research Theme: Optimization of matrix product calculation in convolution calculation of depth learning using
low rank approximation
Motivation
By using the low rank approximation, it is expected to
reduce the calculation / data volume in CNN training /
reasoning while maintaining high recognition performanc
Indeed in the inference of 20 layers of ResNet
Successfully reduce matrix rank by 50% while maintaining recognition
accuracy
Issue of CNN
feature of CNN
Extensive calculation time is required for
convolution calculation (sum of products of
matrices)
Recognition performance is preserved by single
precision or half precision calculation

5. Motivation 5
Network characteristics (GoogleNet)
A neural network model showing the highest image recognition rate in ILSVRC 2014. It has a characteristic
configuration that it consists of 22 layers of convolution layers and does not have a total binding layer. Because of
this, cuDNN's performance is well represented, so it is often used in benchmarking. It is a model often used for
image recognition.
GoogleNet

6. 6
Research Theme: Optimization of matrix product calculation in convolution calculation of depth learning using
low rank approximation
Motivation
By using the low rank approximation, it is expected to
reduce the calculation / data volume in CNN training /
reasoning while maintaining high recognition performanc
Indeed in the inference of 20 layers of ResNet
Successfully reduce matrix rank by 50% while maintaining recognition
accuracy
Issue of CNN
feature of CNN
Extensive calculation time is required for
convolution calculation (sum of products of
matrices)
Recognition performance is preserved by single
precision or half precision calculation

7. 7
1. Reduce computational/memory effort
•Reduced memory footprint and is is enable to size up model
•Reduced computational effort and speedup
2. Make neural computation suitable for low-
power dedicated hardware
Motivation
Issue of CNN
feature of CNN
Extensive calculation time is required for
convolution calculation (sum of products of
matrices)
Recognition performance is preserved by single
precision or half precision calculation
Why we want to quantize the neural network
and reduce computational accuracy?

8.
Outline 8
→ Why do you want to quantize the neural network and reduce computational accuracy?
Motivation
→ I introduce 6 methods on numerical precision of parameters
Brief Survey of learning with low precision and quantization
→ based on “CONVNET TRAINING WITH HALF-FLOAT PRECISION” @GTC 2017
Survey NV-caffe-0.16 (16-bit Floating-Point)

9.
Outline 9
→ Why do you want to quantize the neural network and reduce computational accuracy?
Motivation
→ based on “CONVNET TRAINING WITH HALF-FLOAT PRECISION” @GTC 2017
Survey NV-caffe-0.16 (16-bit Floating-Point)
→ I introduce 6 methods on numerical precision of parameters
Brief Survey of learning with low precision and quantization
16-bit Fixed-Point Number
Dynamic Fixed-Point Number
8-bit Approximate Representation
BinaryConnect
BinaryNet
Binary-Weight-Networks
XNOR-Nets
Quantized Neural Networks
16-bit Floating-Point
Deep Learning with Limited Numerical Precision (ICML2015)
Training deep neural networks with low precision multiplications (ICLR 2015)
BinaryConnect: Training Deep Neural Networks with binary weights during propagations
(Advances in Neural Information Processing Systems 2015)
BinaryNet: Training Deep Neural Networks with Weights and Activations Constrained to +1 or −1
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
CONVNET TRAINING WITH HALF-FLOAT PRECISION (GTC 2017)

10. 16-bit Fixed-Point Number
Dynamic Fixed-Point Number
8-bit Approximate Representation
BinaryConnect
BinaryNet
Binary-Weight-Networks
XNOR-Nets
Quantized Neural Networks
16-bit Floating-Point
Deep Learning with Limited Numerical Precision (ICML2015)
Training deep neural networks with low precision multiplications (ICLR 2015)
BinaryConnect: Training Deep Neural Networks with binary weights during propagations
(Advances in Neural Information Processing Systems 2015)
BinaryNet: Training Deep Neural Networks with Weights and Activations Constrained to +1 or −1
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
CONVNET TRAINING WITH HALF-FLOAT PRECISION (GTC 2017)
Brief Survey of deep learning with low precision and quantization

11. 16-bit Fixed-Point Number
Dynamic Fixed-Point Number
8-bit Approximate Representation
BinaryConnect
BinaryNet
Binary-Weight-Networks
XNOR-Nets
Quantized Neural Networks
16-bit Floating-Point
Deep Learning with Limited Numerical Precision (ICML2015)
Training deep neural networks with low precision multiplications (ICLR 2015)
BinaryConnect: Training Deep Neural Networks with binary weights during propagations
(Advances in Neural Information Processing Systems 2015)
BinaryNet: Training Deep Neural Networks with Weights and Activations Constrained to +1 or −1
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
CONVNET TRAINING WITH HALF-FLOAT PRECISION (GTC 2017)
Brief Survey of deep learning with low precision and quantization

12. 12
16-bit Fixed-Point Number
Brief Survey of learning with low precision and quantization
Abstract
With MNIST, CIFAR-10 Dataset
Performed Deep Learning with fixed point (Fixed Point)
operation and verified accuracy and performance and
achieved performance(Accuracy) equivalent to 32 bit
Floating Point with 16 bit Fixed Point operation.
What is amazing point compared to previous studies?
The merit of Fixed point is
· Faster operation than Floating Point (classical high speed
method can be used)
· The GPU can handle only floating-point operations, whereas
FPGAs can handle low-power fixed-point arithmetic
· Reduce consumption of memory (talk on comparison
between 16 bit Fixed Point and 32 bit Floating Point)
Main technique
They propose Round-to-Nearest and Stochastic Round as
two rounding methods, and the latter method achieves
inference accuracy equivalent to that implemented by single
precision floating point operation

13.
IL : Number of integer bits
FL : Number of fractional bits
WL = IL + FL
13
16-bit Fixed-Point Number
Brief Survey of learning with low precision and quantization
Experiment method · ResultMain technique
They propose Round-to-Nearest and Stochastic Round as
two rounding methods, and the latter method achieves
inference accuracy equivalent to that implemented by single
precision floating point operation
MNIST(CNN)
CIFAR10(CNN)
Discussion
Depending on the problem setting, you have to change FL
and do various tuning
Recently CUDA and cuDNN support 16 bit floating point, so
there is not much memory saving effect compared with it

14. 16-bit Fixed-Point Number
Dynamic Fixed-Point Number
8-bit Approximate Representation
BinaryConnect
BinaryNet
Binary-Weight-Networks
XNOR-Nets
Quantized Neural Networks
16-bit Floating-Point
Deep Learning with Limited Numerical Precision (ICML2015)
Training deep neural networks with low precision multiplications (ICLR 2015)
BinaryConnect: Training Deep Neural Networks with binary weights during propagations
(Advances in Neural Information Processing Systems 2015)
BinaryNet: Training Deep Neural Networks with Weights and Activations Constrained to +1 or −1
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
CONVNET TRAINING WITH HALF-FLOAT PRECISION (GTC 2017)
Brief Survey of deep learning with low precision and quantization

15. 15
Dynamic Fixed-Point Number
Brief Survey of learning with low precision and quantization
Abstract
With MNIST, CIFAR-10, SVHN(The Street View House
Numbers) Dataset
For each of the three data sets and each of the three
formats(floating-point,fixed-point 16,dynamic fixed-point
16), the effect of multiplication accuracy on the final error
of training is evaluated. Network is Maxout.
What is amazing point compared to previous studies?
Results that it is better to change Scaling Factor with error
rate with Dynamic Fixed Point
For the first time to train a dynamic fixed-point deep neural
network.
Main technique
In learning of DNN, the variables have the following features
· Values range of activations, gradients, parameters are
different
· Gradients gradually decrease during learning
In fixed point format, it is not suitable for DNN.
Dynamic fixed point format is a scheme with a scaling factor
for each group.
Each scaling factor is held as an
initial value, and it is updated at
a certain frequency.

16. 16Brief Survey of learning with low precision and quantization
Experiment method · ResultMain technique
Discussion
For the Dynamic Fixed Point, it is the first time to change
the Scaling Factor by the Error Rate
Dynamic Fixed-Point Number
For each of the
three data sets and
each of the three
formats, the effect
of multiplication
accuracy on the
final error of
training is
evaluatedThe integer part is dynamically changing the width of the
decimal part, assuming that parameters and vectors of
arbitrary layers are common. Measure the overflow rate,
increase the decimal part by 1 bit when it is smaller than the
parameter or vector, and change the exponent part
dynamically by decreasing the decimal part by 1 bit when it
is larger than 2 times. By setting the fraction part width to
about 10 bits at the time of forward propagation and back
propagation, and 12 bits at parameter update, we realize an
error rate not different from single precision.

17. 16-bit Fixed-Point Number
Dynamic Fixed-Point Number
8-bit Approximate Representation
BinaryConnect
BinaryNet
Binary-Weight-Networks
XNOR-Nets
Quantized Neural Networks
16-bit Floating-Point
Deep Learning with Limited Numerical Precision (ICML2015)
Training deep neural networks with low precision multiplications (ICLR 2015)
BinaryConnect: Training Deep Neural Networks with binary weights during propagations
(Advances in Neural Information Processing Systems 2015)
BinaryNet: Training Deep Neural Networks with Weights and Activations Constrained to +1 or −1
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
CONVNET TRAINING WITH HALF-FLOAT PRECISION (GTC 2017)
Brief Survey of deep learning with low precision and quantization

18. 18
BinaryConnect
Brief Survey of learning with low precision and quantization
Abstract
With MNIST, CIFAR-10, SVHN Dataset
BinaryConnect: The weight matrix itself is held as a
continuous value of real numbers, and the weight
matrix is binarized (+1 or -1) at the time of forward /
backward calculation,
The training time is tripled and the memory quantity is
1/16 (only for weight)
What is amazing point compared to previous studies?
Binary weight for forward / backward calculation
Main technique
Classifying the learning process as forward propagation, backward
propagation, update, forward propagation and backward
propagation binarize weight and update uses real number
The reason for using update as a real number is that the amount
of change in parameter is very small

19. 19Brief Survey of learning with low precision and quantization
Main technique Discussion
If the range
of input and
output
values can
also be
binarized,
the matrix
product
calculation
will be
considerabl
y faster
Parameters such as weights are real numbers, but when
they are forward propagated and back propagated, a
parameter is input to HardSigmoid and the obtained value is
calculated as a value of either +1 or -1 at the boundary of
0.5. It is set to -1 when the value of Hard sigmoid is 0.5 or
less, and to +1 when it is larger than 0.5. Upon updating
parameters, clipping processing is performed using the
original real number and then updated.
BinaryConnect
Experiments on MNIST, CIFAR 10, SVHN
Only using real weights learned at the time of estimation
(Faster learning has been utilized)
· No deterioration in performance due to binarization can be
seen compared with No regularization of general structure
· In the result of CIFAR - 10, the error rate of BinaryConnect
(Stochastic binarization) is the lowest. As performance
improves better than No regularizer, we can see that
generalization performance is improved by binarization.
Experiment method · Result

20. 16-bit Fixed-Point Number
Dynamic Fixed-Point Number
8-bit Approximate Representation
BinaryConnect
BinaryNet
Binary-Weight-Networks
XNOR-Nets
Quantized Neural Networks
16-bit Floating-Point
Deep Learning with Limited Numerical Precision (ICML2015)
Training deep neural networks with low precision multiplications (ICLR 2015)
BinaryConnect: Training Deep Neural Networks with binary weights during propagations
(Advances in Neural Information Processing Systems 2015)
BinaryNet: Training Deep Neural Networks with Weights and Activations Constrained to +1 or −1
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
CONVNET TRAINING WITH HALF-FLOAT PRECISION (GTC 2017)
Brief Survey of deep learning with low precision and quantization

21. 21
BinaryNet
Brief Survey of learning with low precision and quantization
Abstract
The binarization itself of the weight matrix itself adopts the
deterministic method. It seems that speed is important.
The input to each layer shall come in binary. Before
binarizing the output, apply Batch Normalization.
Unfortunately, in terms of accuracy, A bit losing to
BinaryConnect.
What is amazing point compared to previous studies?
A network in which all weights and node outputs are binarized
- In the conventional method (BinaryConnect), only the weight
is binarized
Acceleration by binary operation
- Approximately 7x with GPU calculation (MNIST benchmark)
Main technique
For the gradient calculation, letting notation f (x) f (x) denote
the function used for binarization, f (x) f (x) is usually
differentiated when calculating the gradient, Only when
computing, let f (x) f (x) be a function as follows.

22. 22Brief Survey of learning with low precision and quantization
Experiment method · Result
Main technique
Discussion
that calculation of the neural network can be greatly
speeded up by constructing dedicated hardware
If we simply binarize it, there is a problem
that the gradient becomes 0 and it can not
be learned, but a gradient is calculated using
an approximate method called a straight-
through estimator.
XNOR is added for each "activation function
output x weight" and added
BinaryNet
The table below shows better performance
as the value is smaller with Error Rate. The
top three are also networks using Binary, the
bottom is not Binary. The result of BinaryNet
is the best among those using Binary, and
values close to Deep L2-SVM which is not
Binary appear.
Forward calculation
speed when
optimizing with
XNOR kernel
Speed comparison
of product of
matrix, speed
comparison of
MNIST, order of
comparison of Error
Rate
If binarization is
performed and
sufficient precision
comes out, there is
a possibility

23. 16-bit Fixed-Point Number
Dynamic Fixed-Point Number
8-bit Approximate Representation
BinaryConnect
BinaryNet
Binary-Weight-Networks
XNOR-Nets
Quantized Neural Networks
16-bit Floating-Point
Deep Learning with Limited Numerical Precision (ICML2015)
Training deep neural networks with low precision multiplications (ICLR 2015)
BinaryConnect: Training Deep Neural Networks with binary weights during propagations
(Advances in Neural Information Processing Systems 2015)
BinaryNet: Training Deep Neural Networks with Weights and Activations Constrained to +1 or −1
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks(ECCV2016)
CONVNET TRAINING WITH HALF-FLOAT PRECISION (GTC 2017)
Brief Survey of deep learning with low precision and quantization

24. 24
Binary-Weight-Net XNOR-Net
Brief Survey of learning with low precision and quantization
Abstract
The target of binarization is weight and input
By binarization memory usage is 1/32, speed is 58x faster
Performance is 16% higher than BinaryConnect and BinaryNet
being compared
What is amazing point compared to previous studies?
If only weights are binarized, it has been shown that even a
difficult task like ImageNet can yield considerable accuracy
(-3%)
As a new technique, scaling factor introduced
- Lower run-times and memory (relative to full-precision)
- Higher accuracy (relative to former binary methods)
Main technique
Binary-Weight-Networks (Network that binarizes weights only)
XNOR-Networks (Network that binarizes both weight and input)
Two proposals

25. 25Brief Survey of learning with low precision and quantization
Experiment method · Result
Comparison with
- AlexNet(full (single 32bit float)
precision)
- BinaryNet
- BinaryConnect
Binary-Weight-Net XNOR-Net

26. 26Brief Survey of learning with low precision and quantization
Binary-Weight-Net
Main technique (1), find the binary B and A for the weight
(2), Forward propagation (B ⊕ I) α
(3), Back propagation WW uses binary version W ~
(4), Update parameter W and learning rate (do not use binary value
only at update update)
The reason why binarization is not done at the time of update is that
the updating amount at the time of update is very small, but when
binarizing after updating, these changes disappear and Parameter is
not updated
Once Training is over, real weights are not needed and forward
propagation is performed with only binary weight when estimating

27. 27Brief Survey of learning with low precision and quantization
XNOR-Net
Main technique Both weight and input are binarized. This speeds up the convolution
operation by only XNOR and bitcounting operations
Changes to a structure that error is less likely
to propagate
Speedup using XNOR-
bitcoun
Worth using binary
convolution if computation
speed is important.
If the number of channels &
filter size increase then the
performance gain increases
as well.
XNOR-Nets provide supreme
speedup at a cost of
accuracy

28.
Outline 28
→ Why do you want to quantize the neural network and reduce computational accuracy?
Motivation
→ based on “CONVNET TRAINING WITH HALF-FLOAT PRECISION” @GTC 2017
Survey NV-caffe-0.16 (16-bit Floating-Point)
→ I introduce 6 methods on numerical precision of parameters
Brief Survey of learning with low precision and quantization

29. Survey cuDNN, NVIDIA recent? news

30. Survey cuDNN, NVIDIA recent news 30
FP16 Support
Mixed-Precision Programming with CUDA 8 / Posted on October 19, 2016 by Mark Harris

31. Survey cuDNN, NVIDIA recent news 31
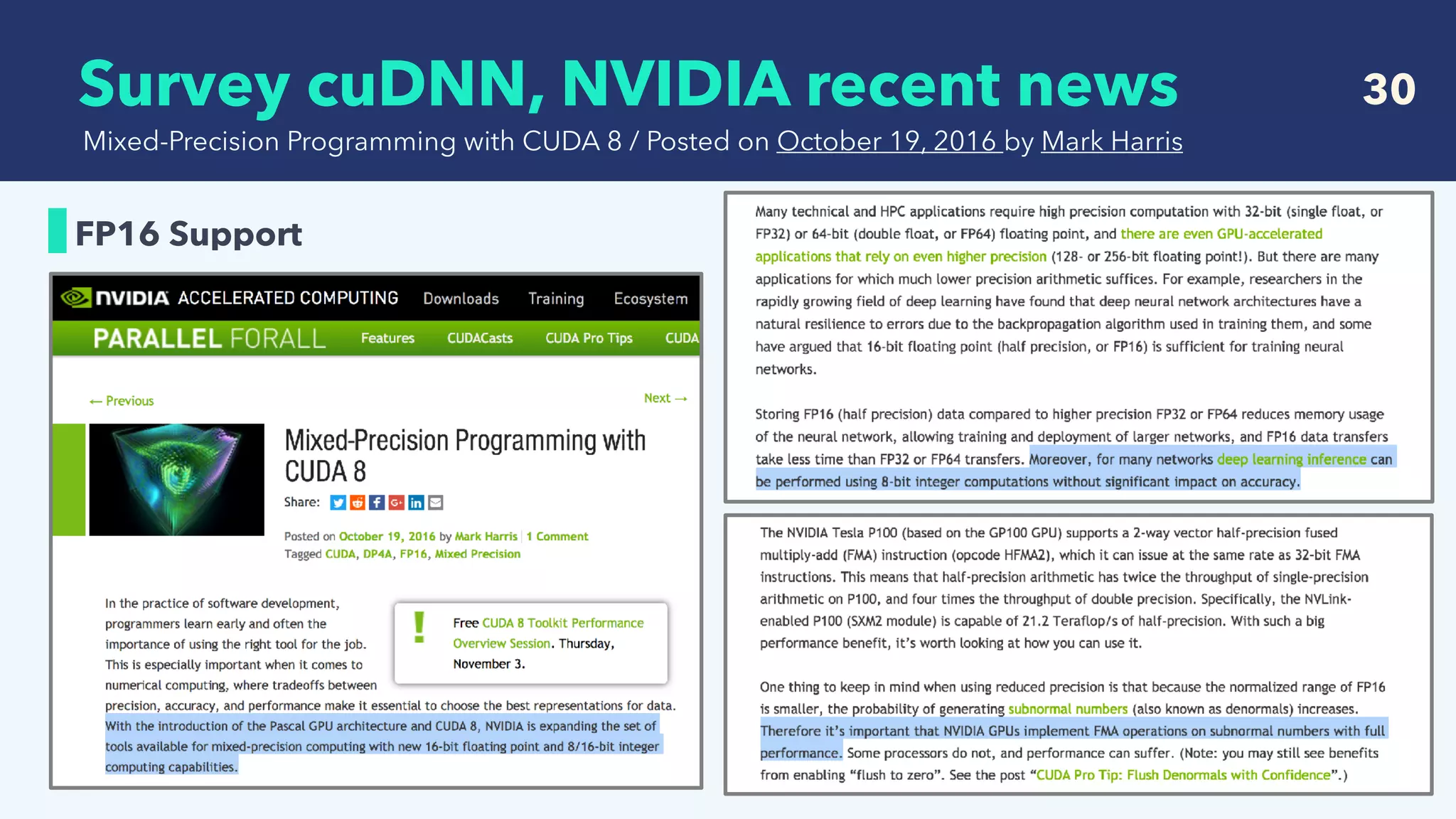
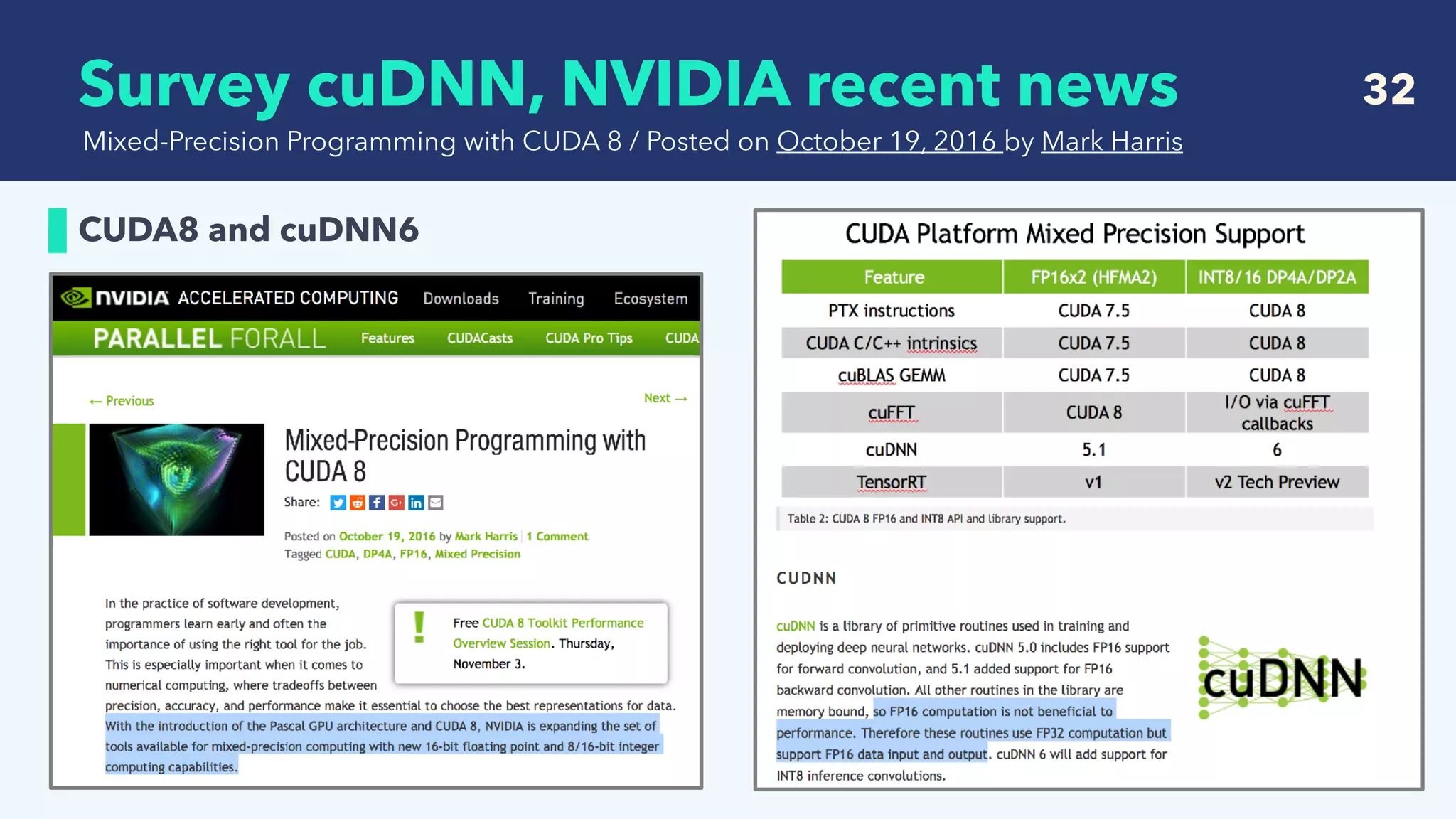
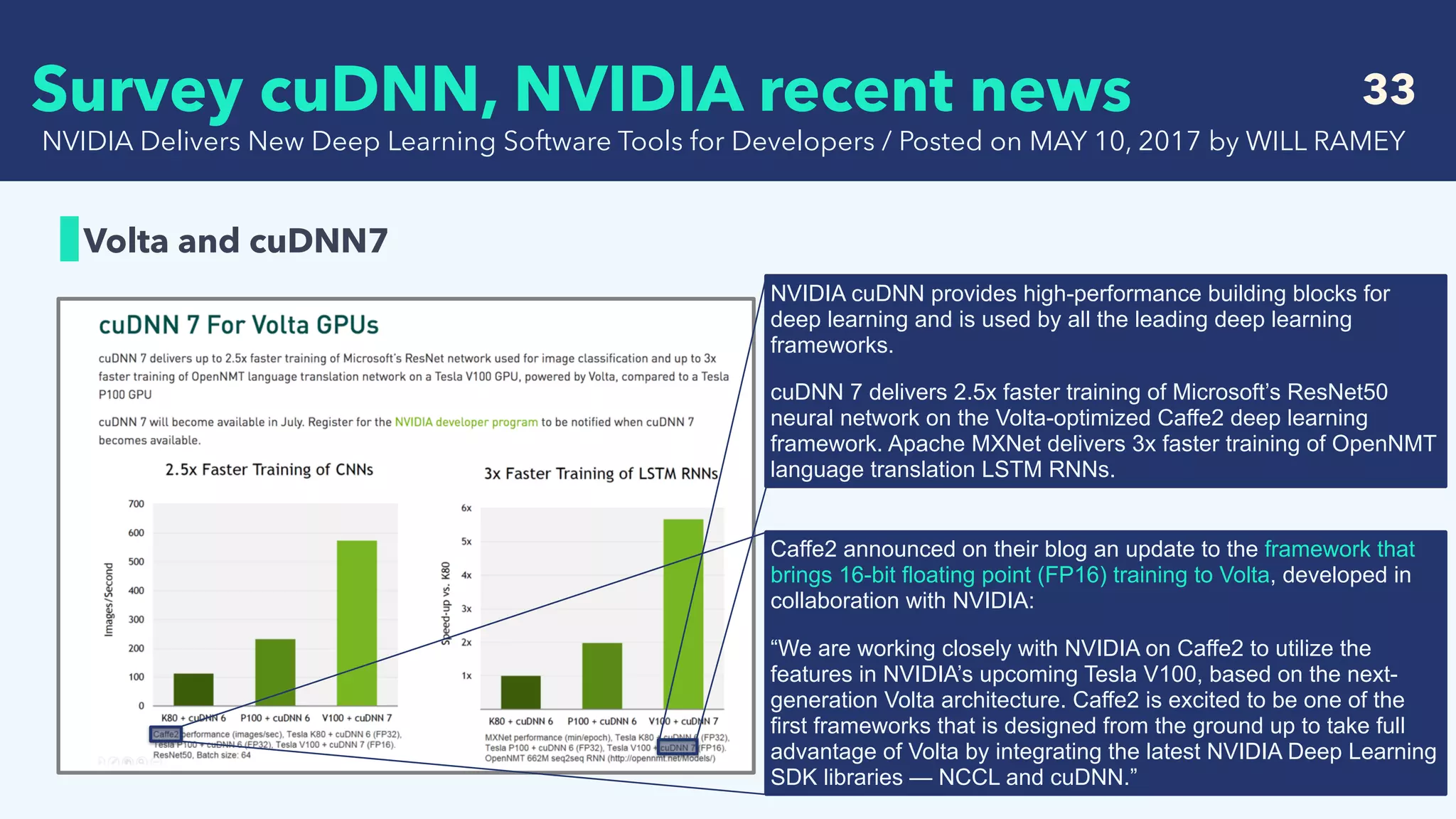
FP16 Support
Mixed-Precision Programming with CUDA 8 / Posted on October 19, 2016 by Mark Harris
A fused multiply–add (sometimes known as FMA or fmadd)[2] is a floating-point multiply–add operation
performed in one step, with a single rounding. That is, where an unfused multiply–add would compute the
product b×c, round it to N significant bits, add the result to a, and round back to N significant bits, a fused
multiply–add would compute the entire expression a+b×c to its full precision before rounding the final result
down to N significant bits.
A fast FMA can speed up and improve the accuracy of many computations that involve the accumulation of
products:
• Dot product
• Matrix multiplication
• Polynomial evaluation (e.g., with Horner's rule)
• Newton's method for evaluating functions.
• Convolutions and artificial neural networks
Fused multiply–add can usually be relied on to give more accurate results. However, William Kahan has
pointed out that it can give problems if used unthinkingly.[3] If x2 − y2 is evaluated as ((x×x) − y×y) using fused
multiply–add, then the result may be negative even when x = y due to the first multiplication discarding low
significance bits. This could then lead to an error if, for instance, the square root of the result is then evaluated.
When implemented inside a microprocessor, an FMA can actually be faster than a multiply operation followed
by an add. However, standard industrial implementations based on the original IBM RS/6000 design require a
2N-bit adder to compute the sum properly.[4][5]
A useful benefit of including this instruction is that it allows an efficient software implementation of division (see
division algorithm) and square root (see methods of computing square roots) operations, thus eliminating the
need for dedicated hardware for those operations.[6]
Fused multiply–add

32. Survey cuDNN, NVIDIA recent news 32
CUDA8 and cuDNN6
Mixed-Precision Programming with CUDA 8 / Posted on October 19, 2016 by Mark Harris

33.
Survey cuDNN, NVIDIA recent news 33
Volta and cuDNN7
NVIDIA Delivers New Deep Learning Software Tools for Developers / Posted on MAY 10, 2017 by WILL RAMEY
NVIDIA cuDNN provides high-performance building blocks for
deep learning and is used by all the leading deep learning
frameworks.
cuDNN 7 delivers 2.5x faster training of Microsoft’s ResNet50
neural network on the Volta-optimized Caffe2 deep learning
framework. Apache MXNet delivers 3x faster training of OpenNMT
language translation LSTM RNNs.
Caffe2 announced on their blog an update to the framework that
brings 16-bit floating point (FP16) training to Volta, developed in
collaboration with NVIDIA:
“We are working closely with NVIDIA on Caffe2 to utilize the
features in NVIDIA’s upcoming Tesla V100, based on the next-
generation Volta architecture. Caffe2 is excited to be one of the
first frameworks that is designed from the ground up to take full
advantage of Volta by integrating the latest NVIDIA Deep Learning
SDK libraries — NCCL and cuDNN.”

34. Survey NV-caffe-0.16 (16-bit Floating-Point)

35. Survey NV-caffe-0.16 (16-bit Floating-Point) 35
Merged fp16 implements in caffe-0.16 branch
NV-caffe : caffe forked by NVIDIA
NVIDIA Caffe (NVIDIA Corporation ©2017) is an NVIDIA-maintained fork of BVLC Caffe tuned for NVIDIA GPUs, particularly in
multi-GPU configurations. Here are the major features:
• 16 bit (half) floating point train and inference support.
• Mixed-precision support. It allows to store and/or compute data in either 64, 32 or 16 bit formats. Precision can be defined
for every layer (forward and backward passes might be different too), or it can be set for the whole Net.
• Integration with cuDNN v6.
• Automatic selection of the best cuDNN convolution algorithm.
• Integration with v1.3.4 of NCCL library for improved multi-GPU scaling.
• Optimized GPU memory management for data and parameters storage, I/O buffers and workspace for convolutional layers.
• Parallel data parser and transformer for improved I/O performance.
• Parallel back propagation and gradient reduction on multi-GPU systems.
• Fast solvers implementation with fused CUDA kernels for weights and history update.
• Multi-GPU test phase for even memory load across multiple GPUs.
• Backward compatibility with BVLC Caffe and NVCaffe 0.15.
• Extended set of optimized models (including 16 bit floating point examples).
NV Caffe

36. 36
Based on the slide of GTC
based on
http://on-demand.gputechconf.com/gtc/2017/presentation/s7218-boris-gainsberg-training-deep-networks-with-half-precision-float.pdf
Survey NV-caffe-0.16 (16-bit Floating-Point)

37. 37
Based on the slide of GTC SUMMARY
1. NVIDIA integrated FLOAT16 training into nvcaffe-0.16
• Float16 data: activations, weights and gradients
• Float16 math: forward and backward pass
• Float16 weight update (no second copy of weights in float)
• Scaling of loss function to prevent underflow and vanishing gradients
2.Trained a number of deep networks (Alexnet, Resnet-50, Inception_v3, ...) with
FLOAT16 without any accuracy loss
3.Memory reduction and speed-up
• Reduced memory footprint and model size up to 2x
• Speed-up upto ~30% (DGX1-Pascal)
Survey NV-caffe-0.16 (16-bit Floating-Point)

38. 38
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
Training with FLOAT16 has many potential benefits
1. Smaller memory footprint:
• ~2x if we keep weights, activations and gradients in FLOAT16 instead FLOAT
2. Faster training:
• compute bounded layers (if HW supports FLOAT16 math - GP100)
• memory bounded layers (ReLU, BatchNorm, ...)
• multi-GPU synchronization
Survey NV-caffe-0.16 (16-bit Floating-Point)

39. 39
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
FLOAT16 has very narrow numerical range
sub-normal (Denormal number)
In the IEEE754 standard, floating point numbers are
represented as binary scientific notation, x = M × 2e.
Here M is the mantissa and e is the exponent.
Mathematically, you can always choose the exponent
so that 1 ≤ M < 2.* However, since in the computer
representation the exponent can only have a finite
range, there are some numbers which are bigger
than zero, but smaller than 1.0 × 2emin. Those
numbers are the subnormals or denormals.
Practically, the mantissa is stored without the
leading 1, since there is always a leading 1, except
for subnormal numbers (and zero). Thus the
interpretation is that if the exponent is non-minimal,
there is an implicit leading 1, and if the exponent is
minimal, there isn't, and the number is subnormal.
Survey NV-caffe-0.16 (16-bit Floating-Point)

40. 40
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
mode
Dfp16
2 copy of weights: float16 for
forward- backward and float for
update
Store data in fp16
Survey NV-caffe-0.16 (16-bit Floating-Point)

41. 41
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
mode
Mfp16 (evolution of Dfp16)
For GPUs with FP16 math
- weight
- activation
- dE/dw(gradient of weight)
- dE/db(gradient of bias)
- dE/dx(gradient of input)
compute in fp16
Survey NV-caffe-0.16 (16-bit Floating-Point)

42. 42
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
mode
Nfp16(evolution of Mfp16)
“Native” float16
To devise Weight Update process
Survey NV-caffe-0.16 (16-bit Floating-Point)

43. 43
Several FP16 Mode
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
Float16 data Dfp16
2 copy of weights: float16 for
forward- backward and float for
update
Float16 math Mfp16 For GPUs with FP16 math
Float16 all Nfp16 “Native” float16
Nvcaffe-0.16, DGX-1, SGD with momentum, 100 epochs, batch=1024, no
augmentation, 1 crop, 1 mode
Why mfp16 is less accurate (-3.7%)?
Survey NV-caffe-0.16 (16-bit Floating-Point)

44. 44
ALEXNET: FLOAT16 MATH
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
Why mfp16 is less accurate (-3.7%)?
Survey NV-caffe-0.16 (16-bit Floating-Point)

45. 45
ALEXNET: FLOAT16 MATH
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
Let’s change backward_math from FLOAT16 to FLOAT
name: "AlexNet_fp16"
default_forward_type: FLOAT16
default_backward_type: FLOAT16
default_forward_math: FLOAT
default_backward_math: FLOAT
layer {
forward_math: FLOAT16
backward_math: FLOAT
}
// 略
solver_data_type: FLOAT16
Accuracy is back! The problem is in the back-propagation
Survey NV-caffe-0.16 (16-bit Floating-Point)

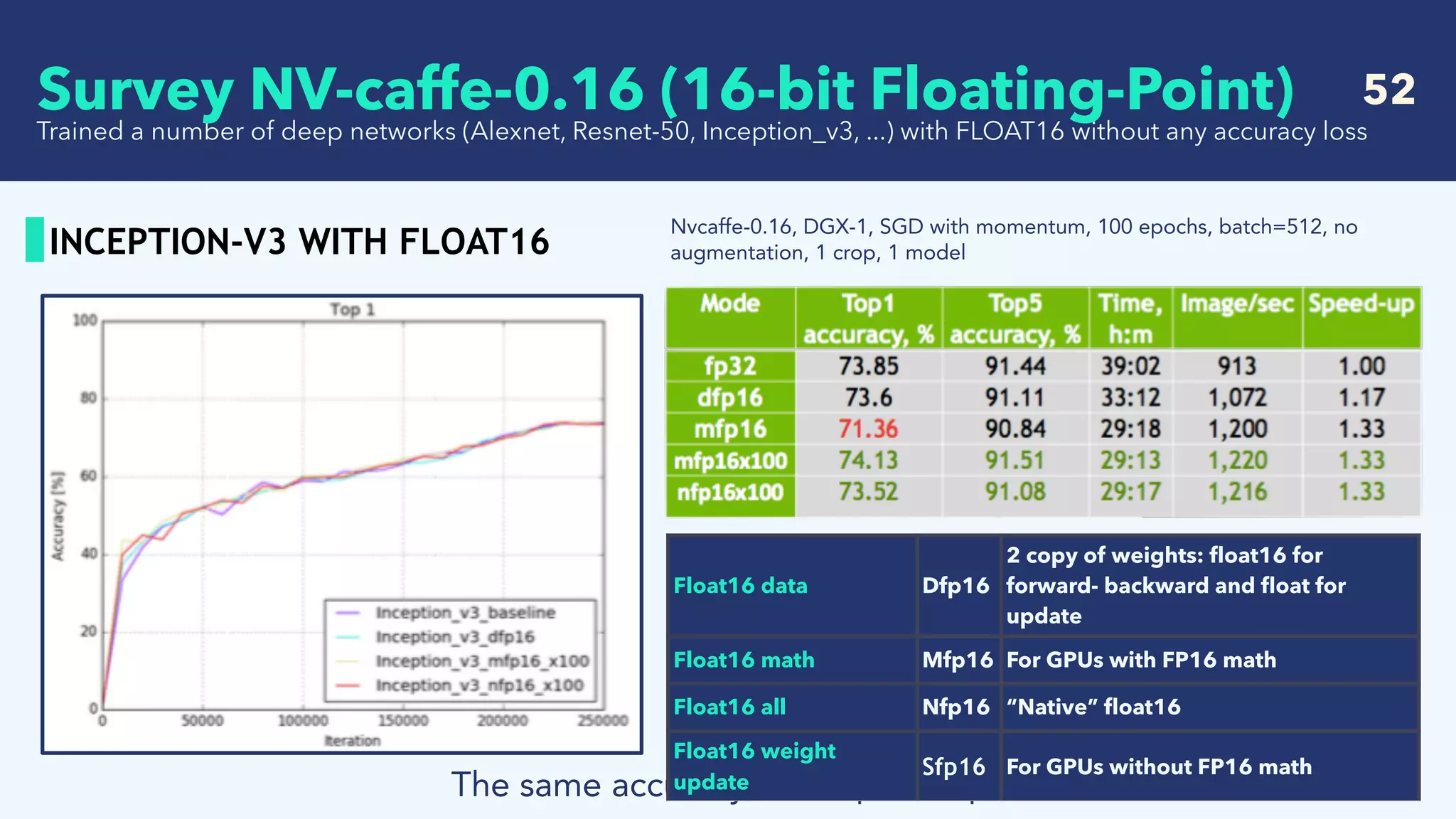
46. 46
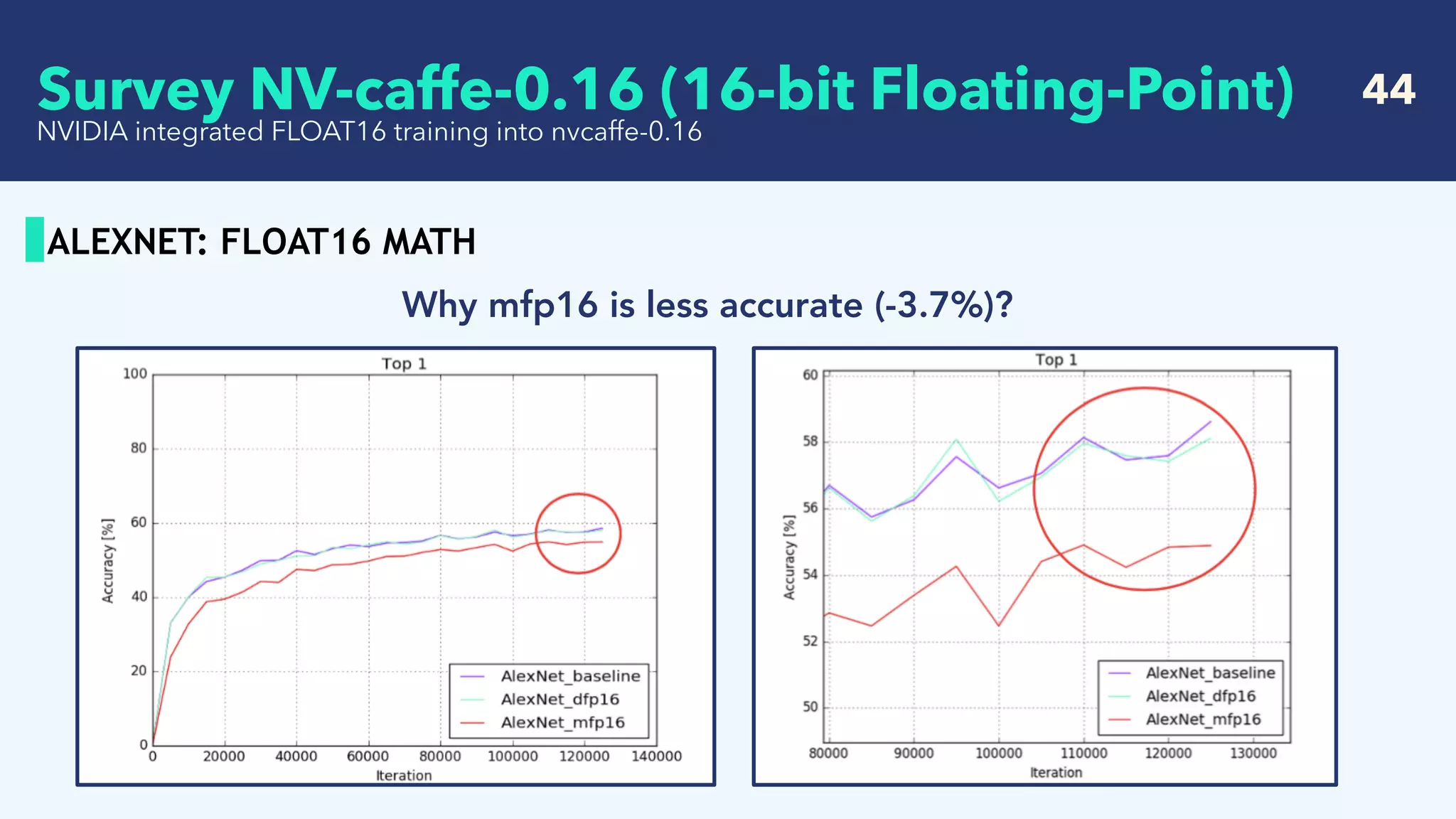
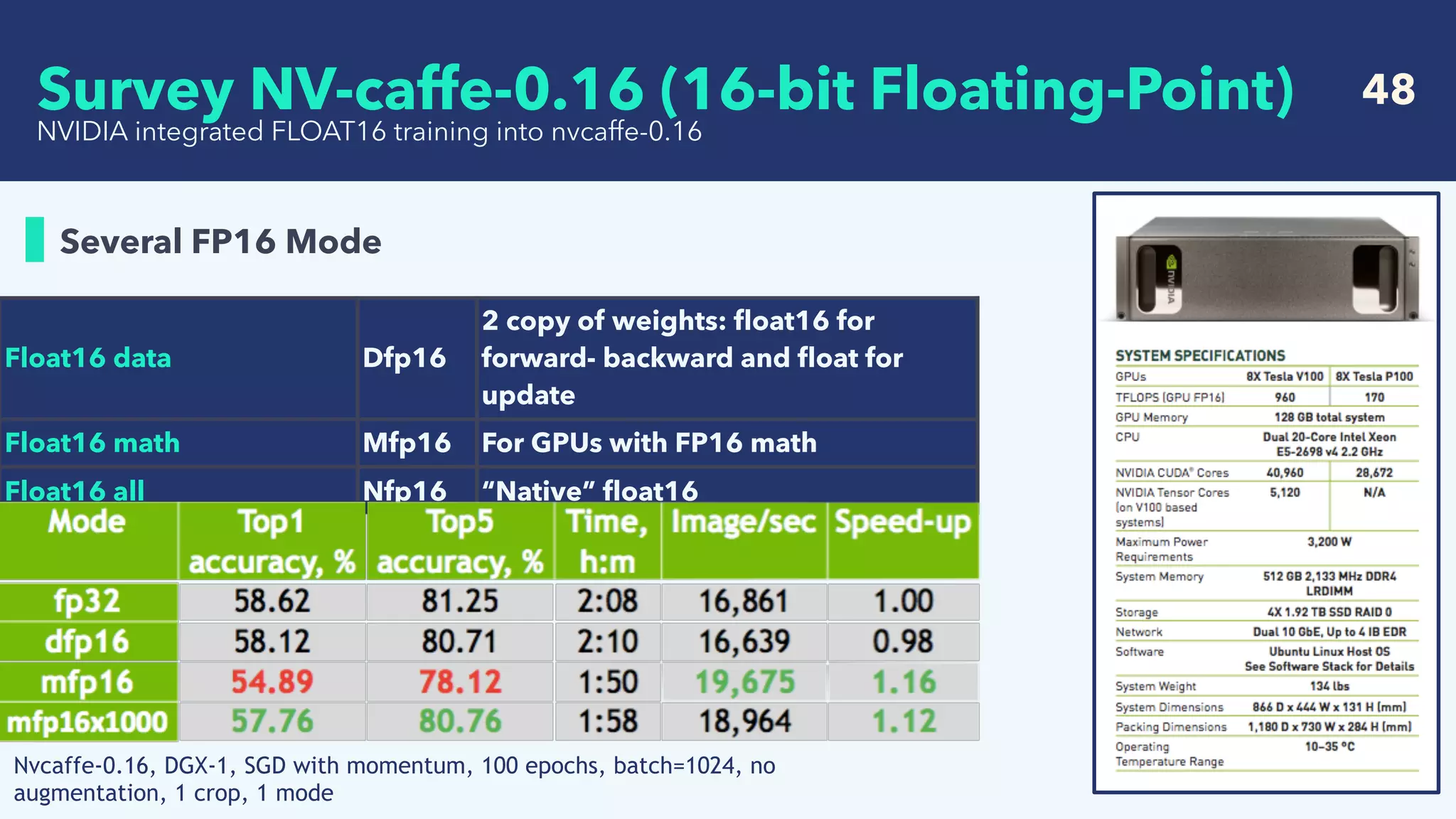
ALEXNET: FLOAT16 MATH
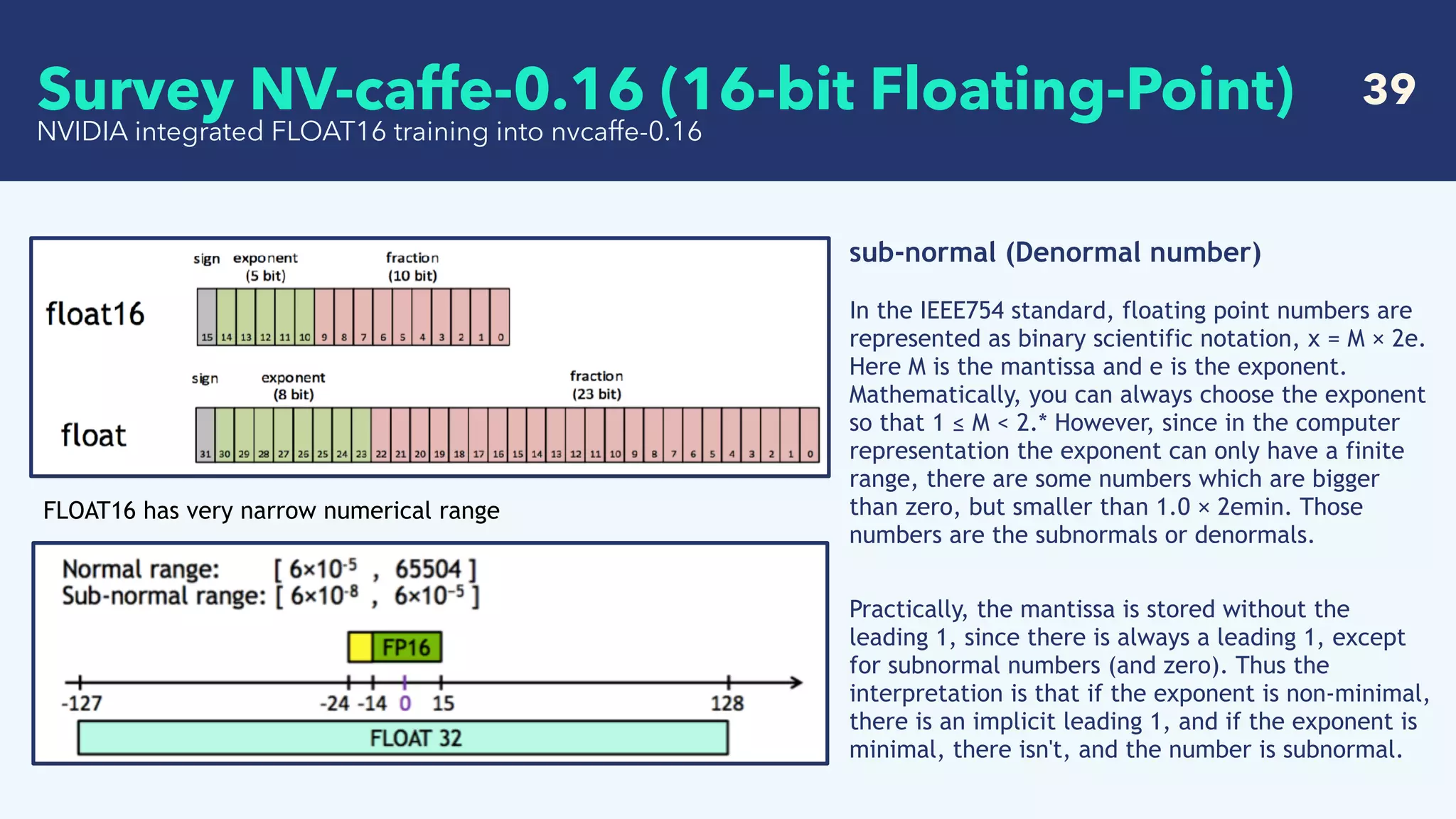
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
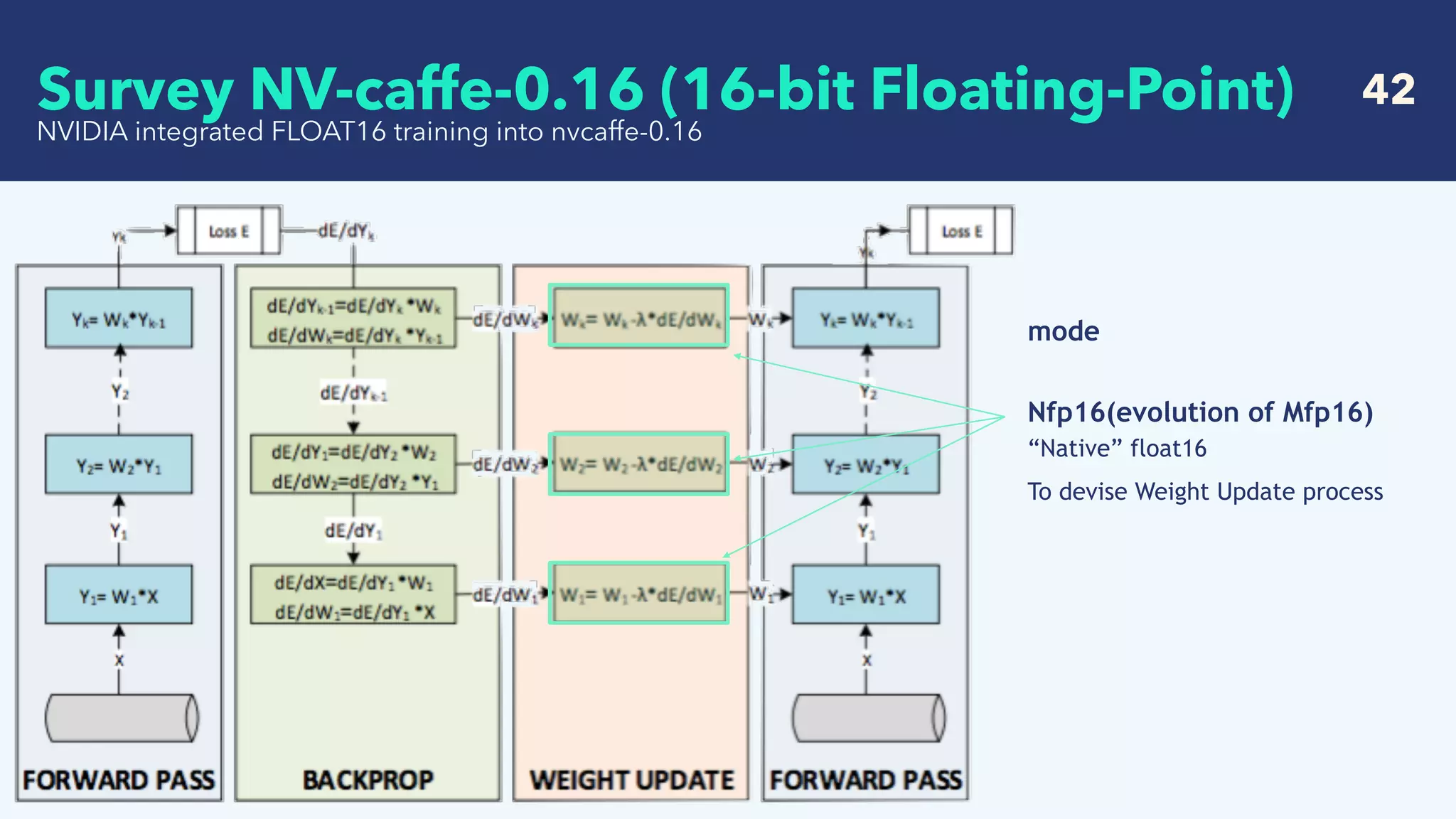
The problem is in the back-propagation
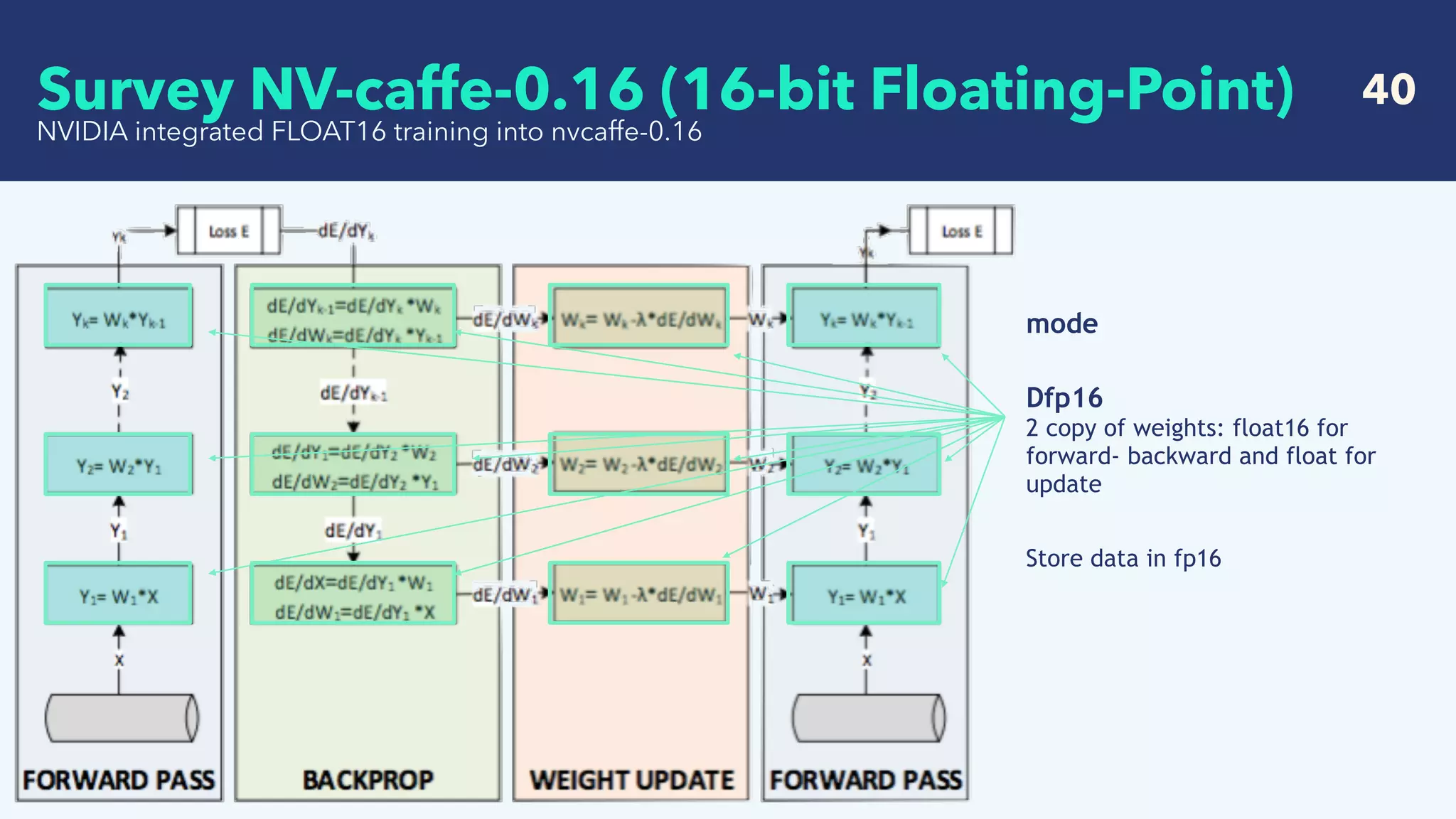
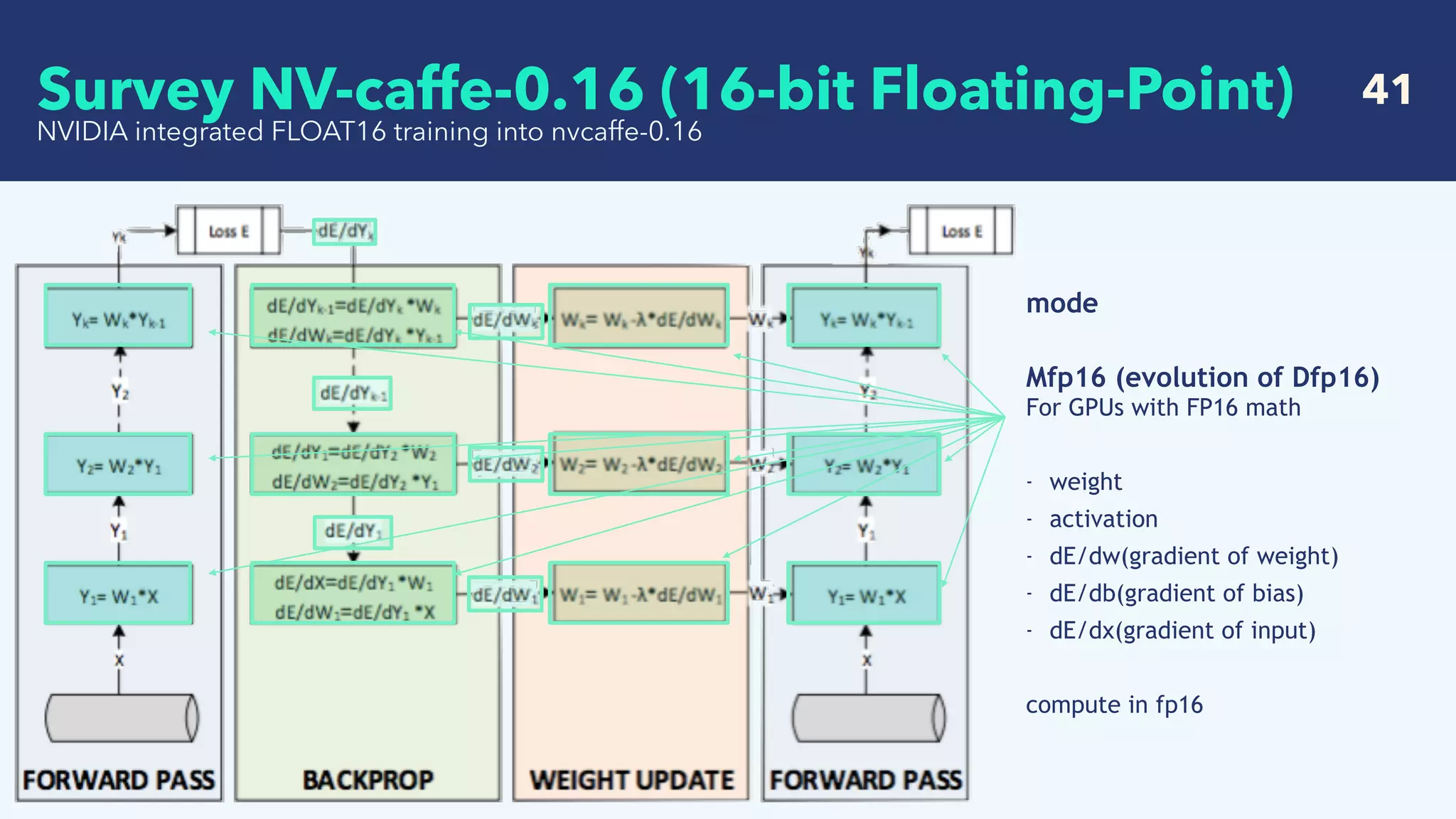
Mfp16
For GPUs with FP16 math
- weight [ok]
- activation [ok]
- dE/dw(gradient of weight) [ok]
- dE/db(gradient of bias) [ok]
- dE/dx(gradient of input) [underflow]
compute in fp16
weights activation dE/dw
dE/dbdE/dx
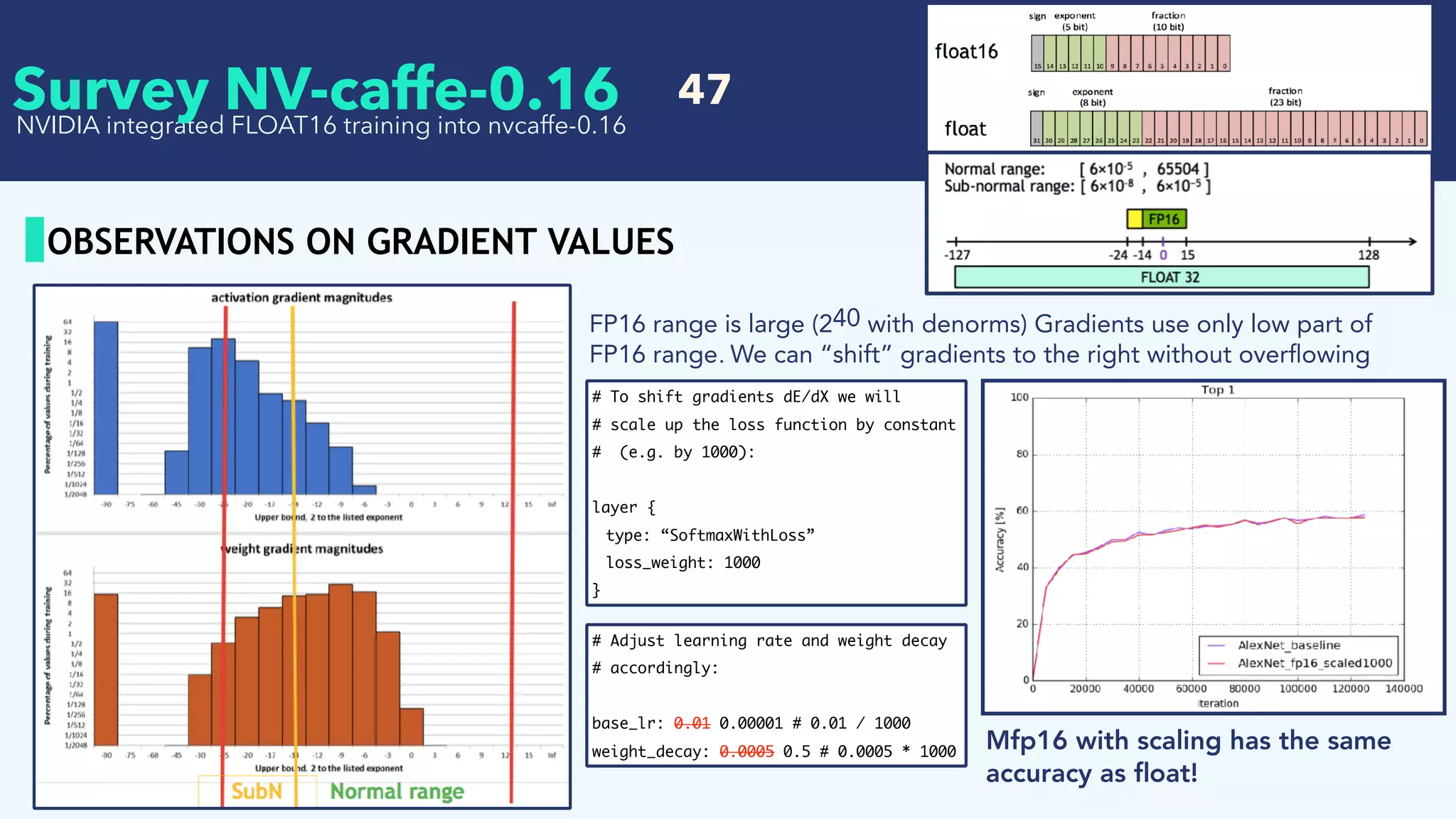
Gradients dE/dx are very small, in the sub-normal range of float16. Potential underflow and loss in
accuracy
Survey NV-caffe-0.16 (16-bit Floating-Point)

47. 47
OBSERVATIONS ON GRADIENT VALUES
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
FP16 range is large (240 with denorms) Gradients use only low part of
FP16 range. We can “shift” gradients to the right without overflowing
# To shift gradients dE/dX we will
# scale up the loss function by constant
# (e.g. by 1000):
layer {
type: “SoftmaxWithLoss”
loss_weight: 1000
}
# Adjust learning rate and weight decay
# accordingly:
base_lr: 0.01 0.00001 # 0.01 / 1000
weight_decay: 0.0005 0.5 # 0.0005 * 1000
Mfp16 with scaling has the same
accuracy as float!
Survey NV-caffe-0.16

48. 48
Several FP16 Mode
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
Float16 data Dfp16
2 copy of weights: float16 for
forward- backward and float for
update
Float16 math Mfp16 For GPUs with FP16 math
Float16 all Nfp16 “Native” float16
Nvcaffe-0.16, DGX-1, SGD with momentum, 100 epochs, batch=1024, no
augmentation, 1 crop, 1 mode
Survey NV-caffe-0.16 (16-bit Floating-Point)

49. 49
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
calculate in FP16
calculate in FP32
(for weight update)
[1] ΔW32(t) =half2float(Δw16(t))
[2] W32(t+1)=W32(t) - λ*ΔW32(t)
[3] W16(t+1)=float2half(W32(t+1))
Survey NV-caffe-0.16 (16-bit Floating-Point)

50. 50
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
calculate in FP16
calculate in FP32
(for weight update)
[1] G16(t+1) = m* G16(t+1) + Δw16(t)
[2] W32=half2float(W16(t))- λ*half2float(G16(t+1))
[3] W16(t+1)=float2half(W32(t+1))
Survey NV-caffe-0.16 (16-bit Floating-Point)

51. 51
ALEXNET : NATIVE FLOAT16
NVIDIA integrated FLOAT16 training into nvcaffe-0.16
1⁄2 memory footprint, 1.16x speed-up, the same accuracy
Float16 data Dfp16
2 copy of weights: float16 for
forward- backward and float for
update
Float16 math Mfp16 For GPUs with FP16 math
Float16 all Nfp16 “Native” float16
Float16 weight
update
Sfp16 For GPUs without FP16 math
Survey NV-caffe-0.16 (16-bit Floating-Point)

52. 52
INCEPTION-V3 WITH FLOAT16
Trained a number of deep networks (Alexnet, Resnet-50, Inception_v3, ...) with FLOAT16 without any accuracy loss
The same accuracy, 33% speed-up
Float16 data Dfp16
2 copy of weights: float16 for
forward- backward and float for
update
Float16 math Mfp16 For GPUs with FP16 math
Float16 all Nfp16 “Native” float16
Float16 weight
update
Sfp16 For GPUs without FP16 math
Nvcaffe-0.16, DGX-1, SGD with momentum, 100 epochs, batch=512, no
augmentation, 1 crop, 1 model
Survey NV-caffe-0.16 (16-bit Floating-Point)

53. 53
RESNET-50 WITH FLOAT16
Trained a number of deep networks (Alexnet, Resnet-50, Inception_v3, ...) with FLOAT16 without any accuracy loss
The same accuracy, 33% speed-up
Float16 data Dfp16
2 copy of weights: float16 for
forward- backward and float for
update
Float16 math Mfp16 For GPUs with FP16 math
Float16 all Nfp16 “Native” float16
Float16 weight
update
Sfp16 For GPUs without FP16 math
Nvcaffe-0.16, DGX-1, SGD with momentum, 100 epochs, batch=512, no
augmentation, 1 crop, 1 model
Survey NV-caffe-0.16 (16-bit Floating-Point)

54. Thanks for your attention