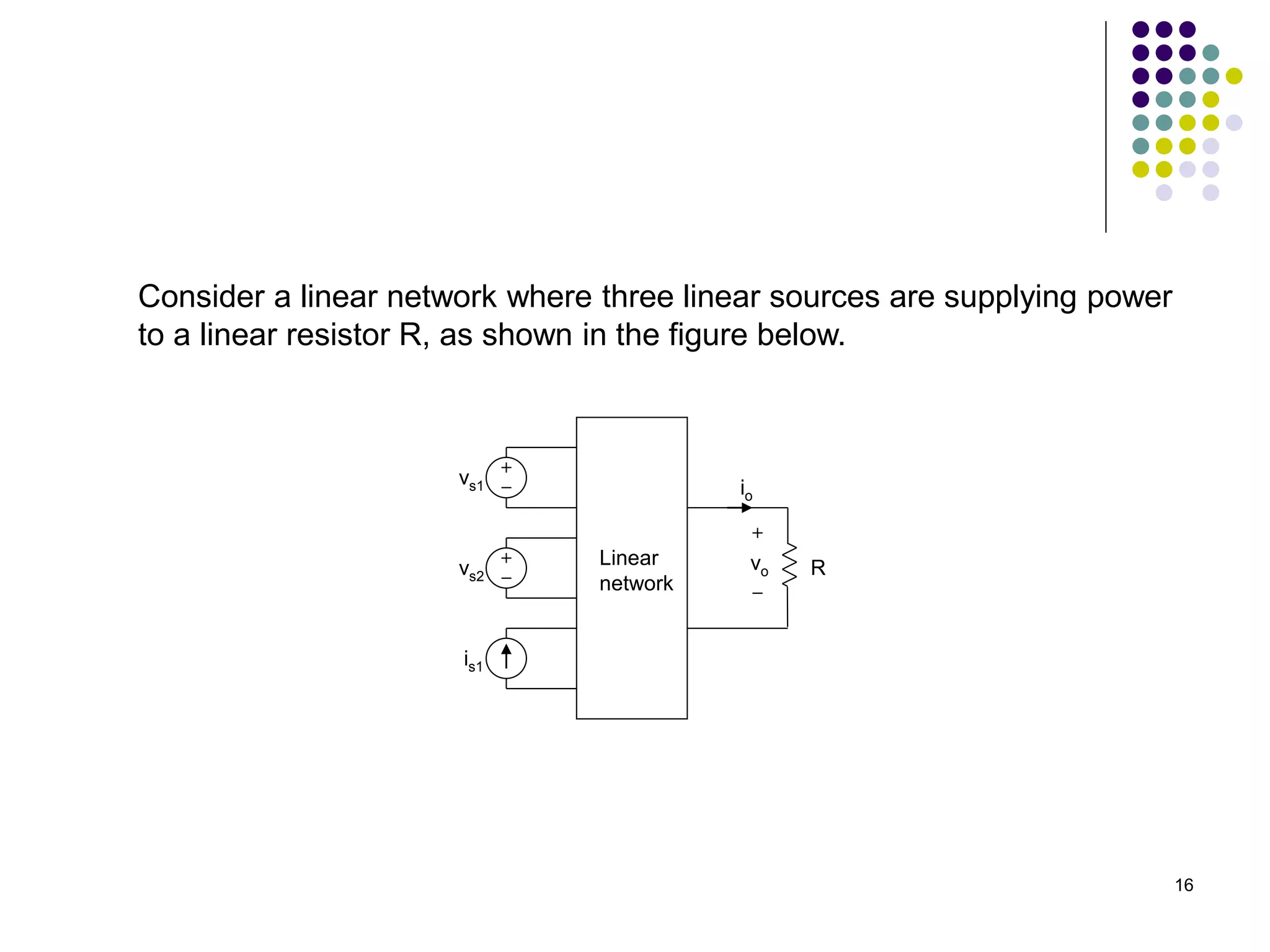
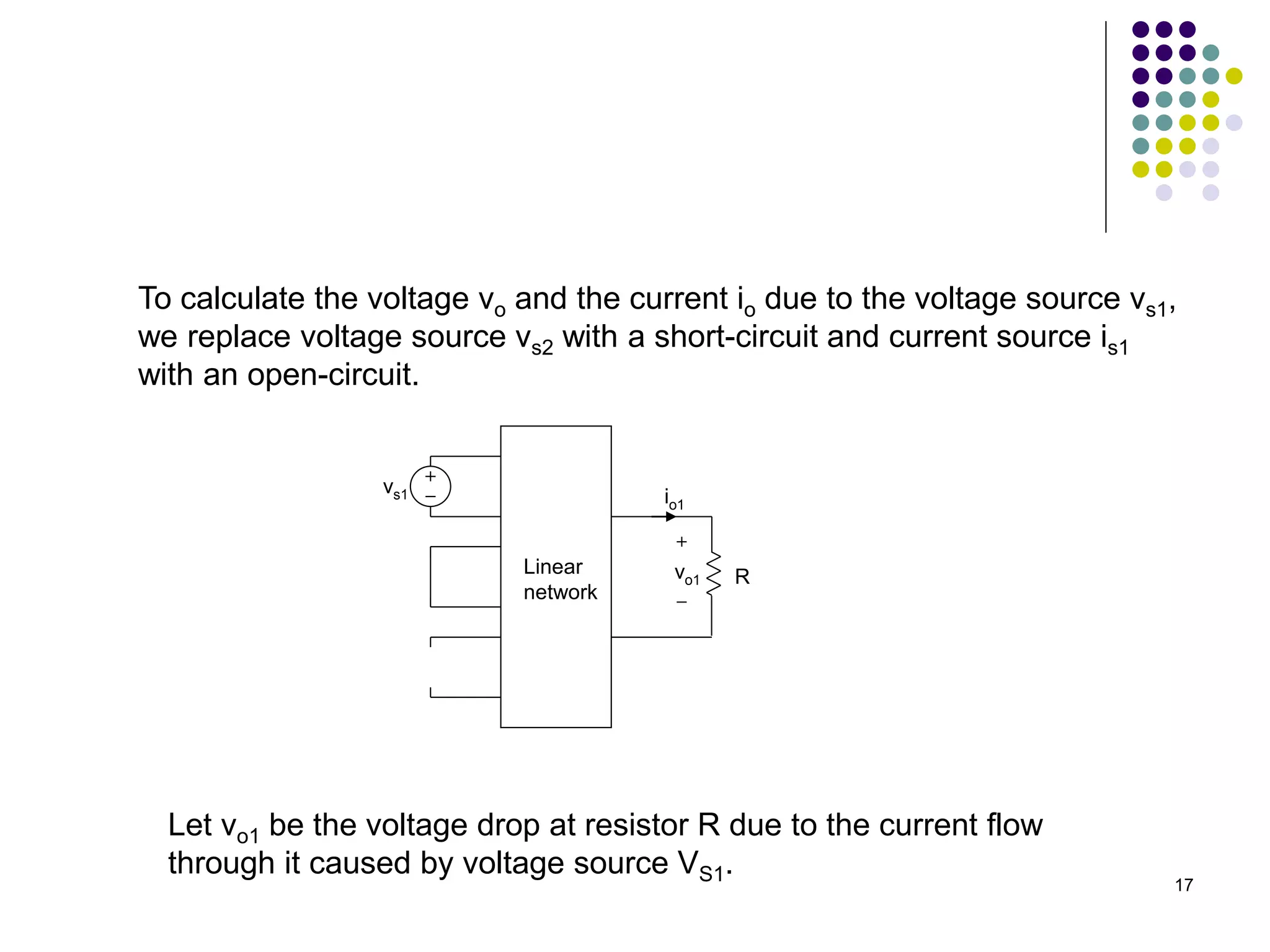
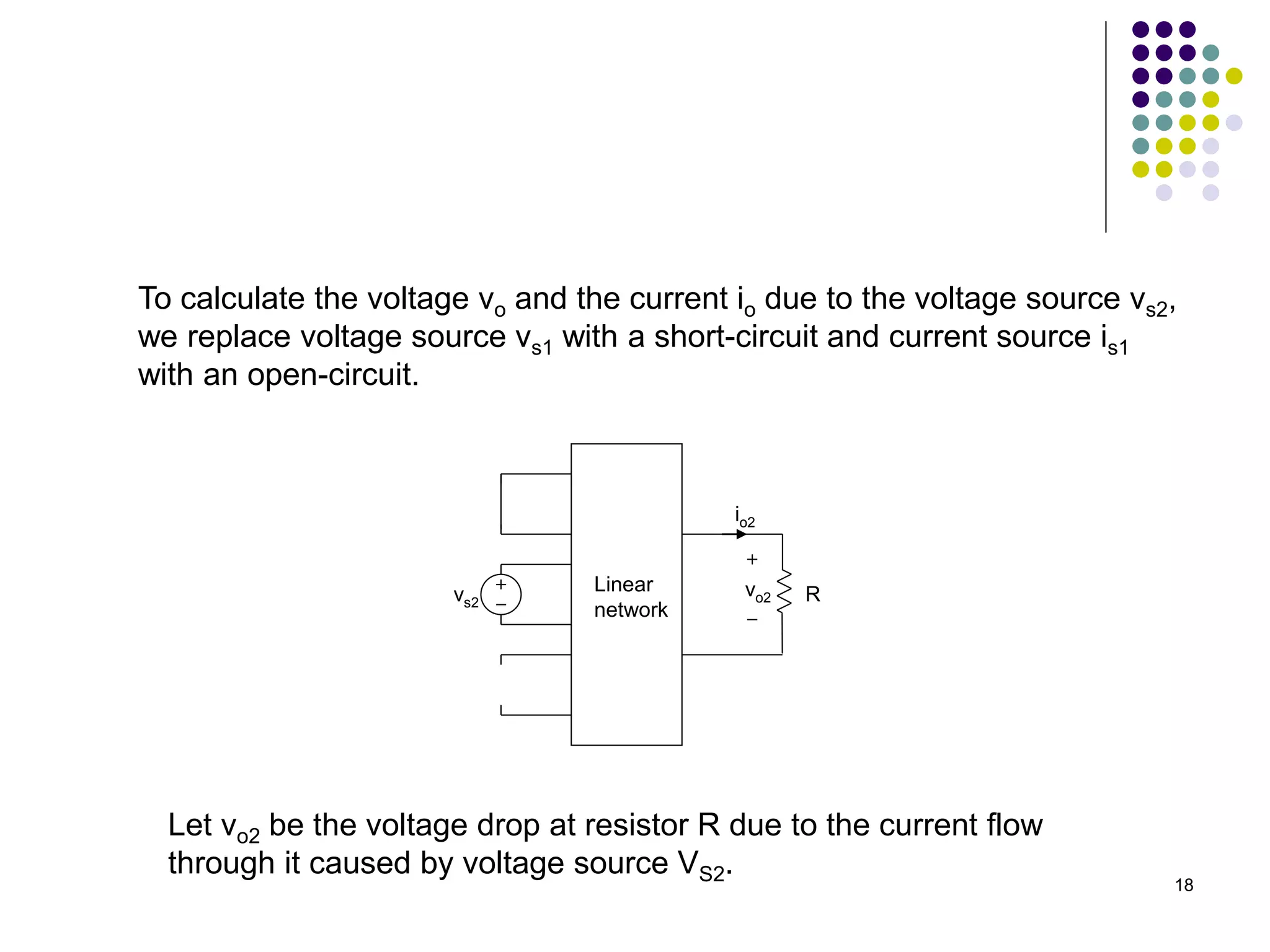
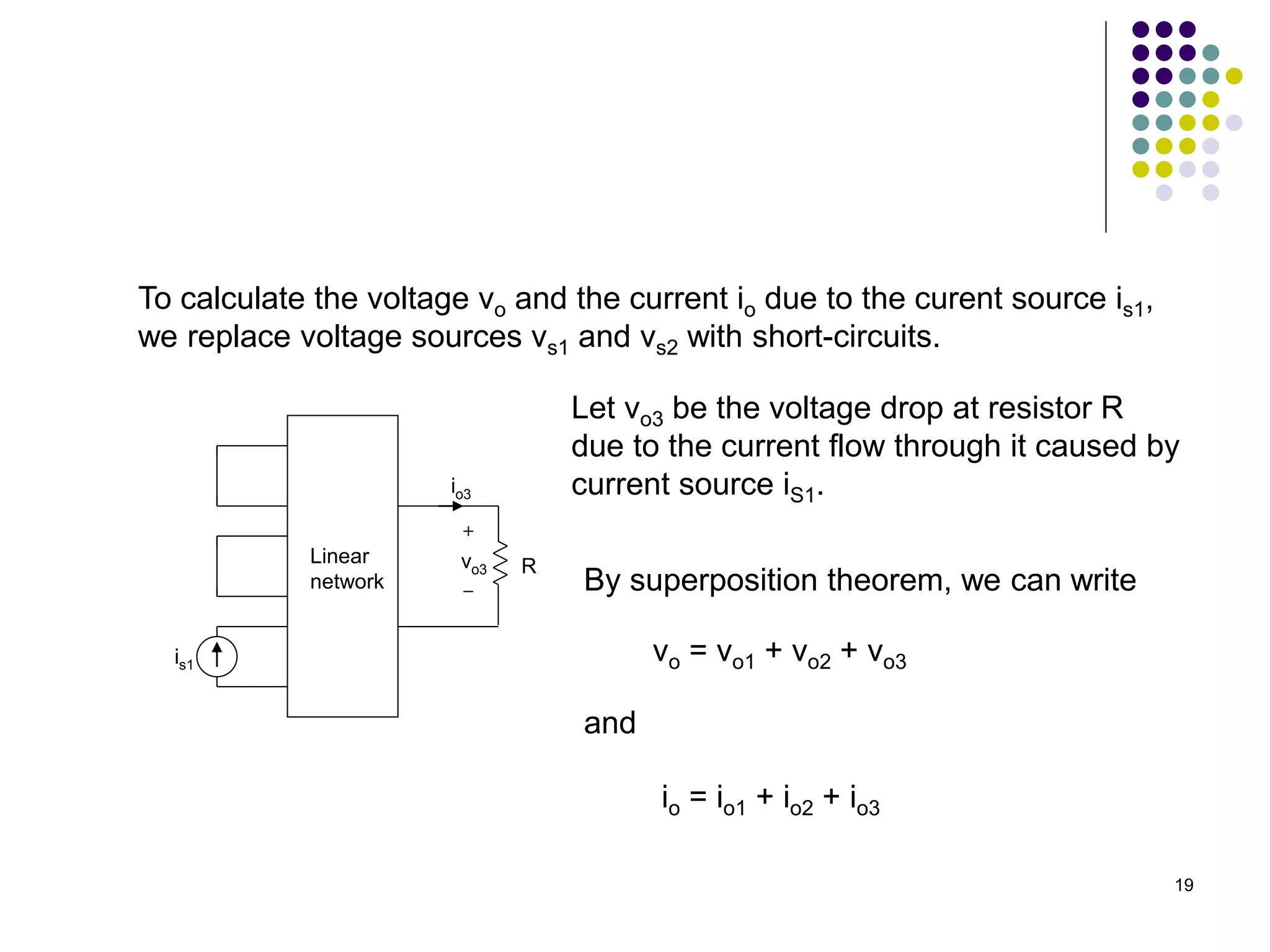
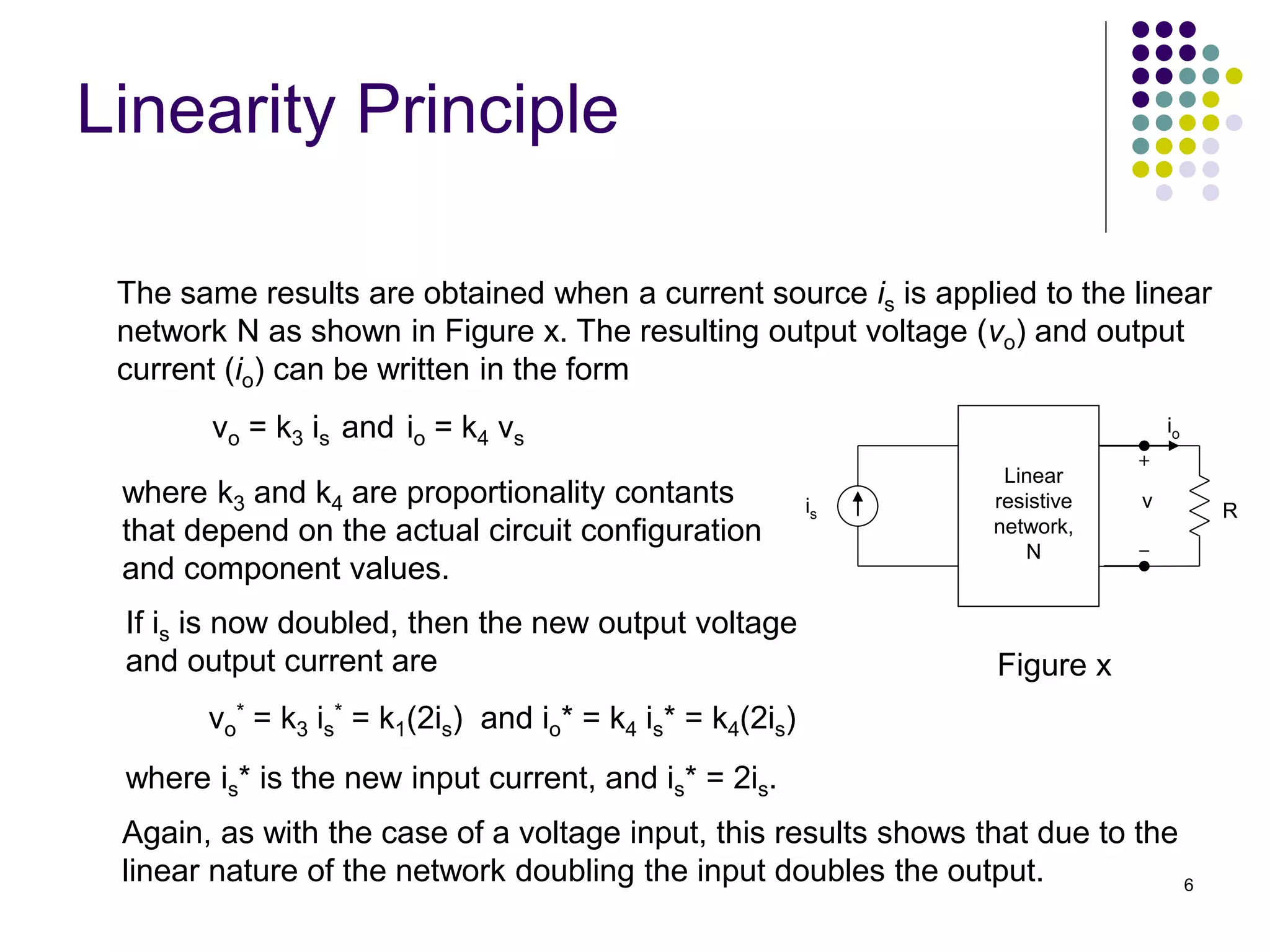
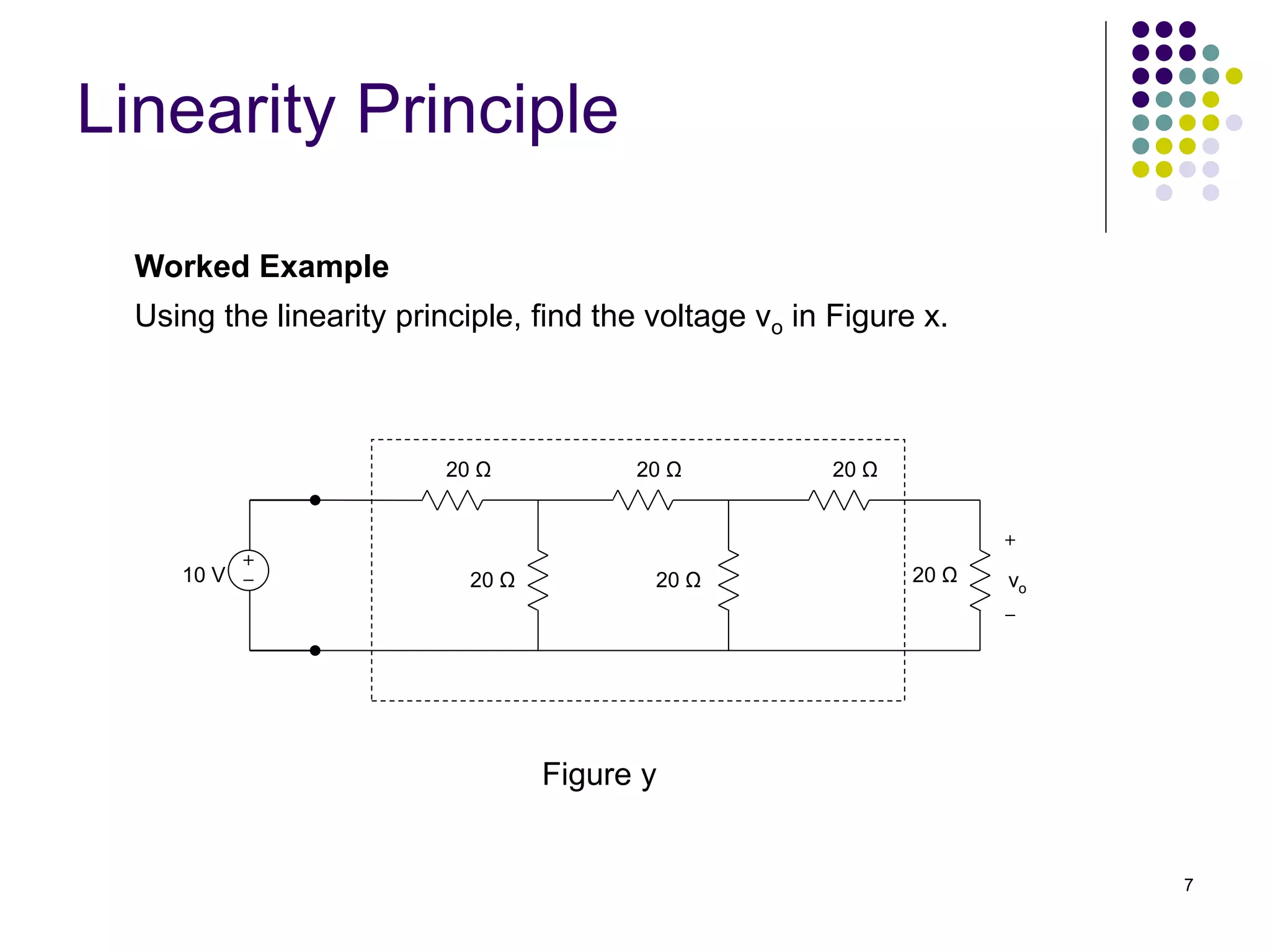
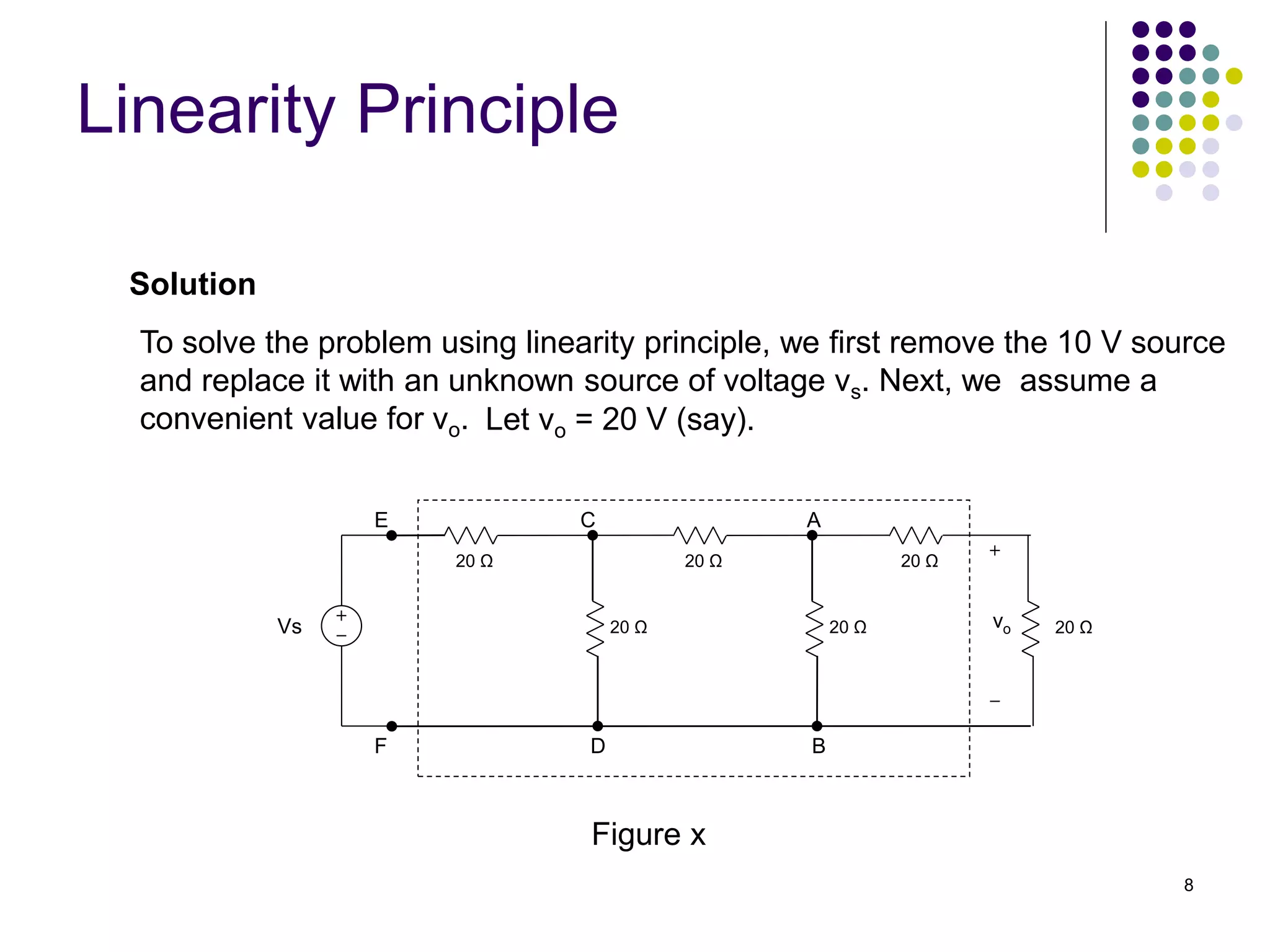
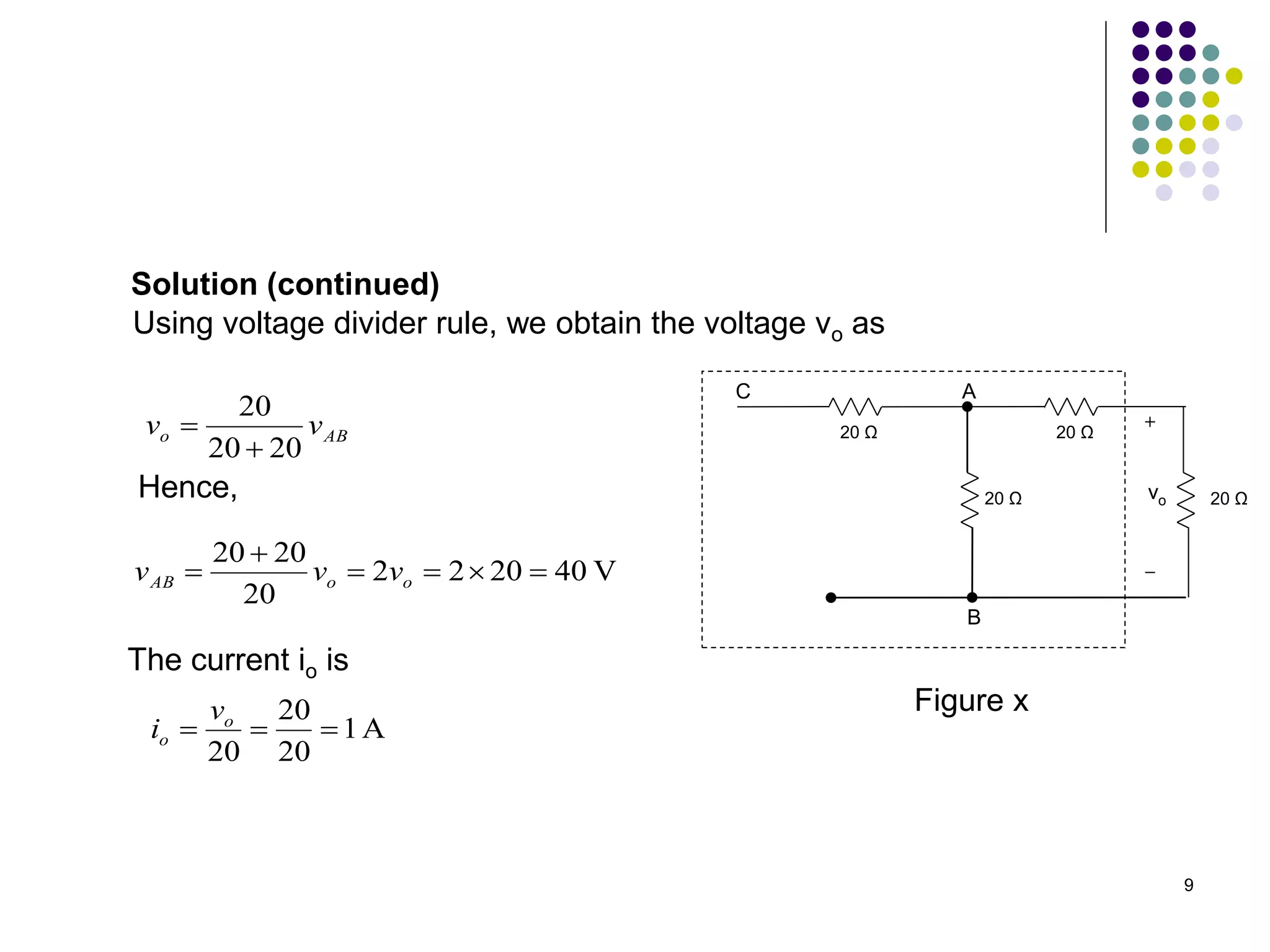
This document discusses linear circuits and techniques for analyzing them, including linearity principle, superposition theorem, and source transformations. It provides examples of using linearity principle to find unknown voltages and currents when an independent source is applied to a linear network. It also provides examples of using superposition theorem to solve for unknowns in a linear circuit with multiple independent sources by considering each source individually.

1. Week 7
Linearity and
Superposition Principles

2. 2
Learning Outcomes
After completing this module, you will be able to:
1. Apply the principle of linearity to linear circuits containing linear resistors
and independent sources to solve for unknown voltages and currents.
2. Apply the principle of superposition to linear circuits containing linear
resistors and independent sources to solve for unknown voltages and
currents.
3. Compute Thevenin’s and Norton’s equivalent circuits for networks
containing resistors and independent sources.
4. Apply source transformations techniques to circuits containing resistors
and independent sources to solve for unknown voltages and currents

3. 3
In this topic we will learn three techniques for analysing linear resistive
circuits. The circuit analysis techniques are:
i. Linearity principle
ii. Superposition theorem
iii. Source transformations

4. 4
A linear network is a circuit composed entirely of independent sources, linear
dependent sources, and linear elements.
One important consequence of linearity is
that a proportionality relationship exists
between one circuit variable and another . Linear
resistive
network,
N
vs R
io
v
Figure x
Let us develop the linearity principle by
considering first the network of Figure x,
which contains an independent source, a
voltage generator, that applies a voltage vs
at the input of the network.
Linearity Principle

5. 5
where k1 and k2 are proportionality contants
that depend on the actual circuit configuration
and component values.
vo = k1 vs
The resulting voltage (vo) and current (io) (response or output) can be written in
the form
and
io = k2 vs
If vs is now doubled, then the new output voltage and output current are
vo
* = k1 vs
* = k1(2vs)
io* = k2 vs* = k2(2vs)
These results show that due to the linear nature of the circuit, doubling the
input doubles the output. This is the linearity principle.
Linear
resistive
network,
N
vs R
io
v
Linearity Principle

6. 6
The same results are obtained when a current source is is applied to the linear
network N as shown in Figure x. The resulting output voltage (vo) and output
current (io) can be written in the form
vo = k3 is and io = k4 vs
Linear
resistive
network,
N
is R
io
v
where k3 and k4 are proportionality contants
that depend on the actual circuit configuration
and component values.
If is is now doubled, then the new output voltage
and output current are
vo
* = k3 is
* = k1(2is) and io* = k4 is* = k4(2is)
where is* is the new input current, and is* = 2is.
Again, as with the case of a voltage input, this results shows that due to the
linear nature of the network doubling the input doubles the output.
Figure x
Linearity Principle

7. 7
Worked Example
Using the linearity principle, find the voltage vo in Figure x.
Linearity Principle
Figure y
10 V
20 Ω
20 Ω
20 Ω
20 Ω
20 Ω
20 Ω vo

8. 8
Solution
To solve the problem using linearity principle, we first remove the 10 V source
and replace it with an unknown source of voltage vs. Next, we assume a
convenient value for vo. Let vo = 20 V (say).
Linearity Principle
20 Ω 20 Ω
20 Ω
20 Ω
vo
Vs 20 Ω 20 Ω
A
B
C
D
E
F
Figure x

9. 9
V
40
20
2
2
20
20
20





 o
o
AB v
v
v
AB
o v
v
20
20
20


Solution (continued)
Using voltage divider rule, we obtain the voltage vo as
Hence,
The current io is
A
1
20
20
20


 o
o
v
i
20 Ω
20 Ω
20 Ω
vo
20 Ω
A
B
C
Figure x

10. 10
Solution (continued)
The current iCA is
A
3
20
40
1
20
o 



 AB
CA
v
i
i
20 Ω 20 Ω
20 Ω
20 Ω
vo
Vs 20 Ω 20 Ω
A
B
C
D
E
F
Figure x :
The voltage vCD is
vCD = vCA + vAB
vCD = (3)(20) + 40 = 100 V
Hence,
The current iEC is
iEC = iCA + iCD = 3 + 100/20 = 8 A

11. 11
Solution (continued)
20 Ω 20 Ω
20 Ω
20 Ω
vo
Vs 20 Ω 20 Ω
A
B
C
D
E
F
Figure x:
The voltage VEF is given by
vEF = vEC + vCD = (8)(20) + 100 = 260 V

12. 12
Solution (continued)
20 Ω 20 Ω
20 Ω
20 Ω
vo
Vs 20 Ω 20 Ω
A
B
C
D
E
F
Figure x:
By the linearity principle, we can write
vo = kvs
where k is a constant of proportionality.
Hence,
20 = k (260) ……. ……….(i)
and
vo = k (10) ……. … …….(ii)

13. 13
Solution (continued)
20 Ω 20 Ω
20 Ω
20 Ω
vo
Vs 20 Ω 20 Ω
A
B
C
D
E
F
Figure x:
Dividing Eq.(i) with Eq.(ii), we obtain
10
260
20

o
v
or,
vo = 20/26 = 0.769 V

14. 14
Exercise
Use the proportionality principle to obtain the voltage vo.
1 Ω
0.5 Ω
3 Ω
vo
E = 10 V 5 Ω 1 Ω
A
B
C
D
E
F
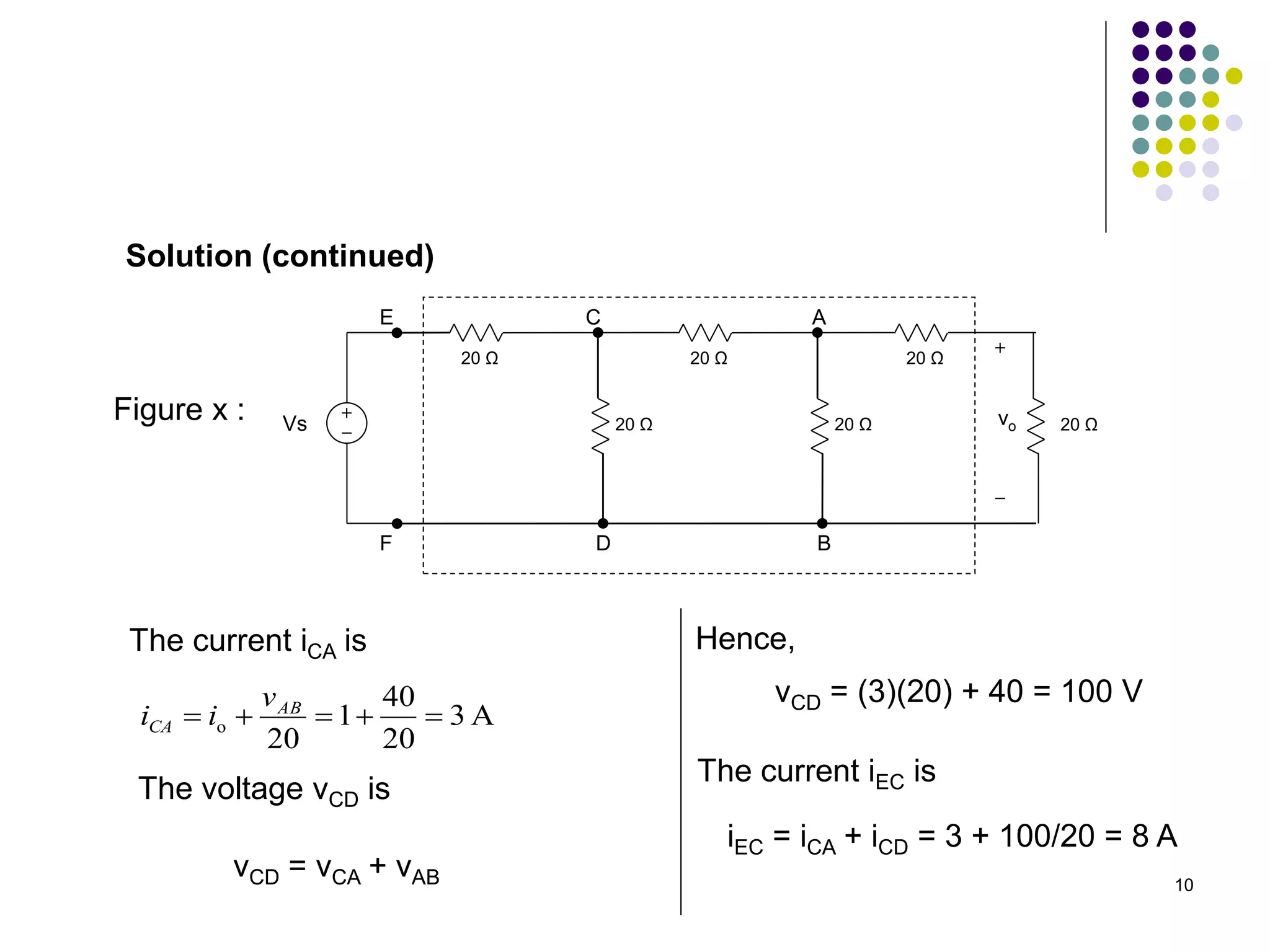
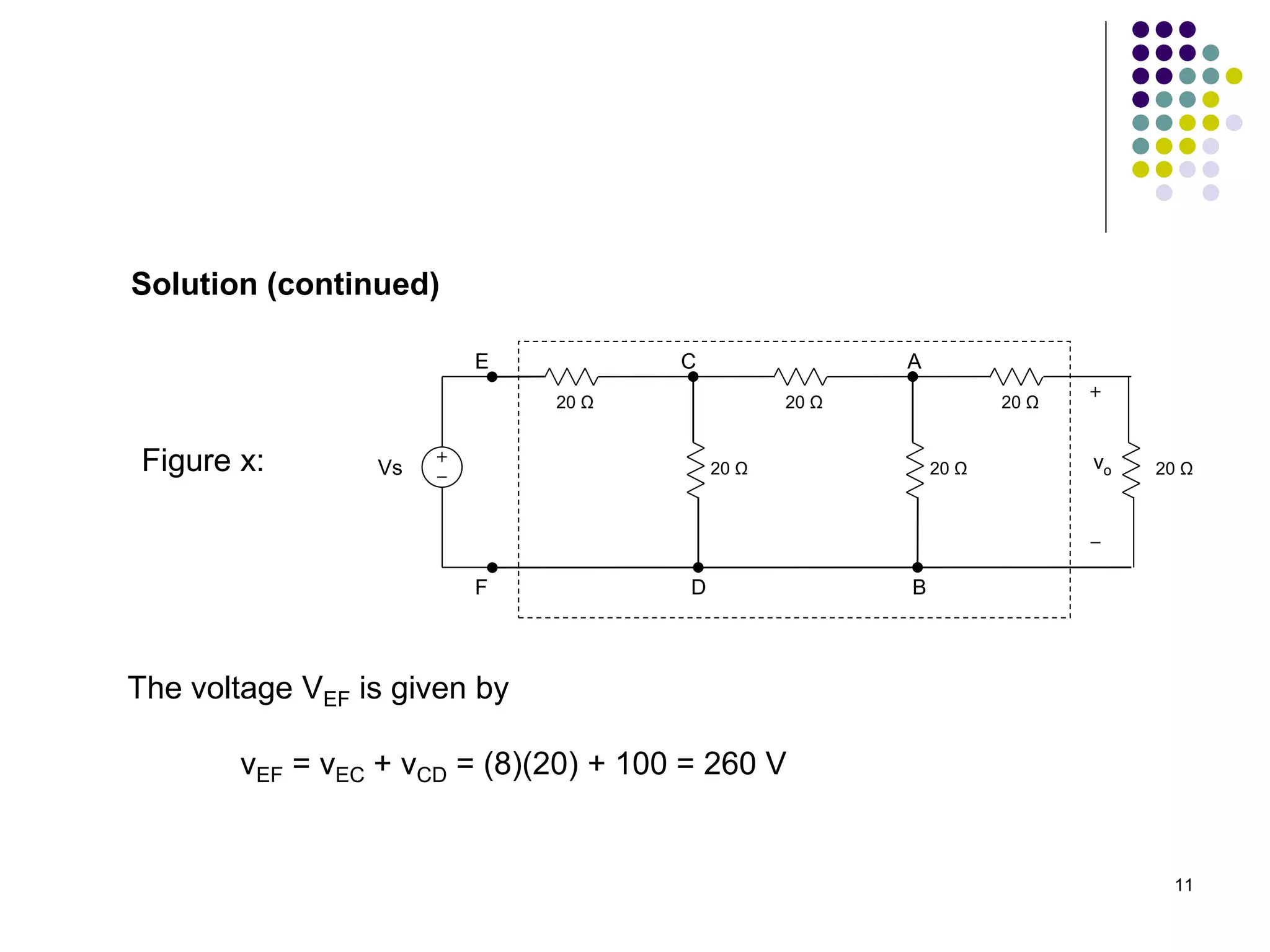
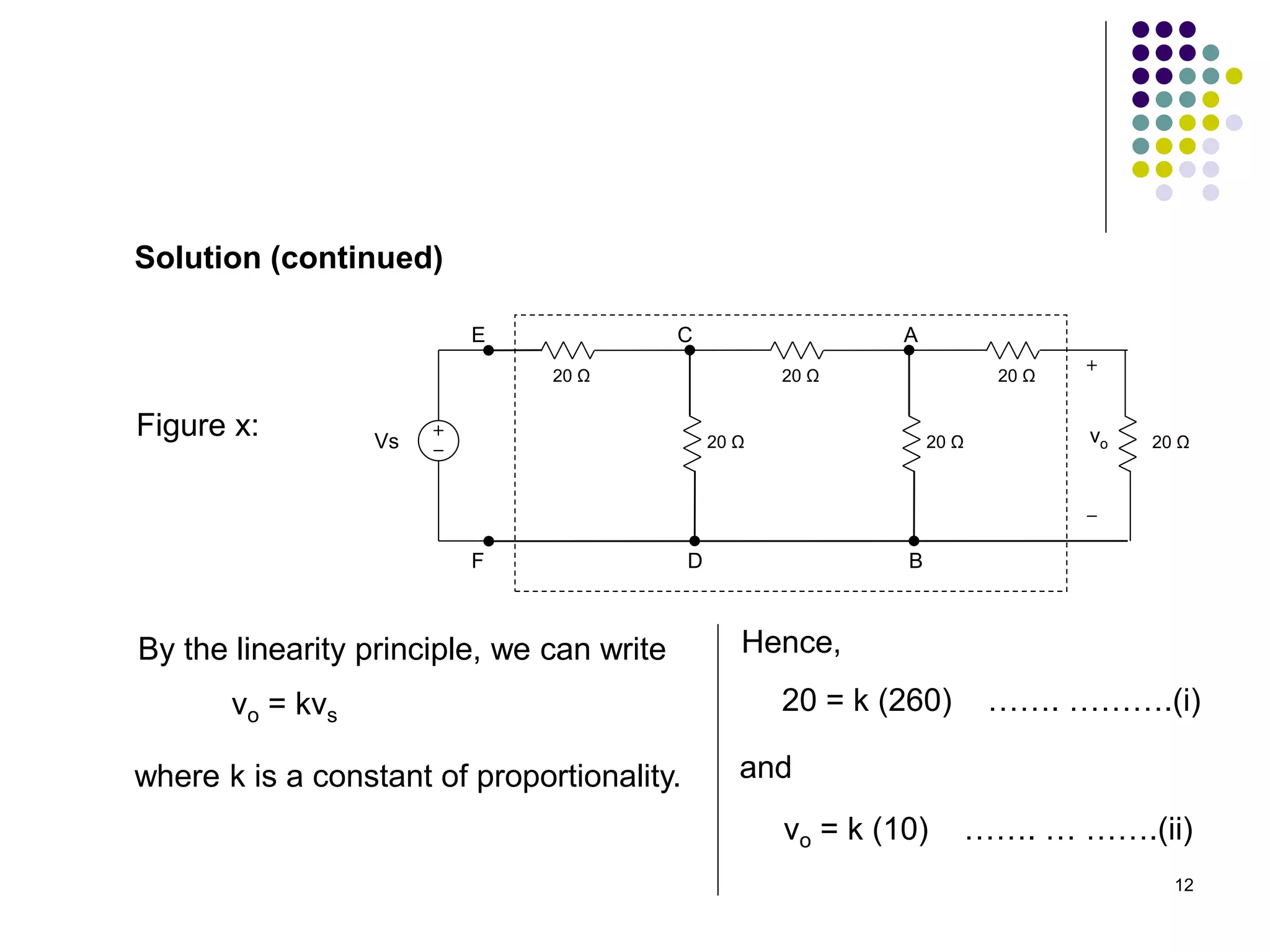
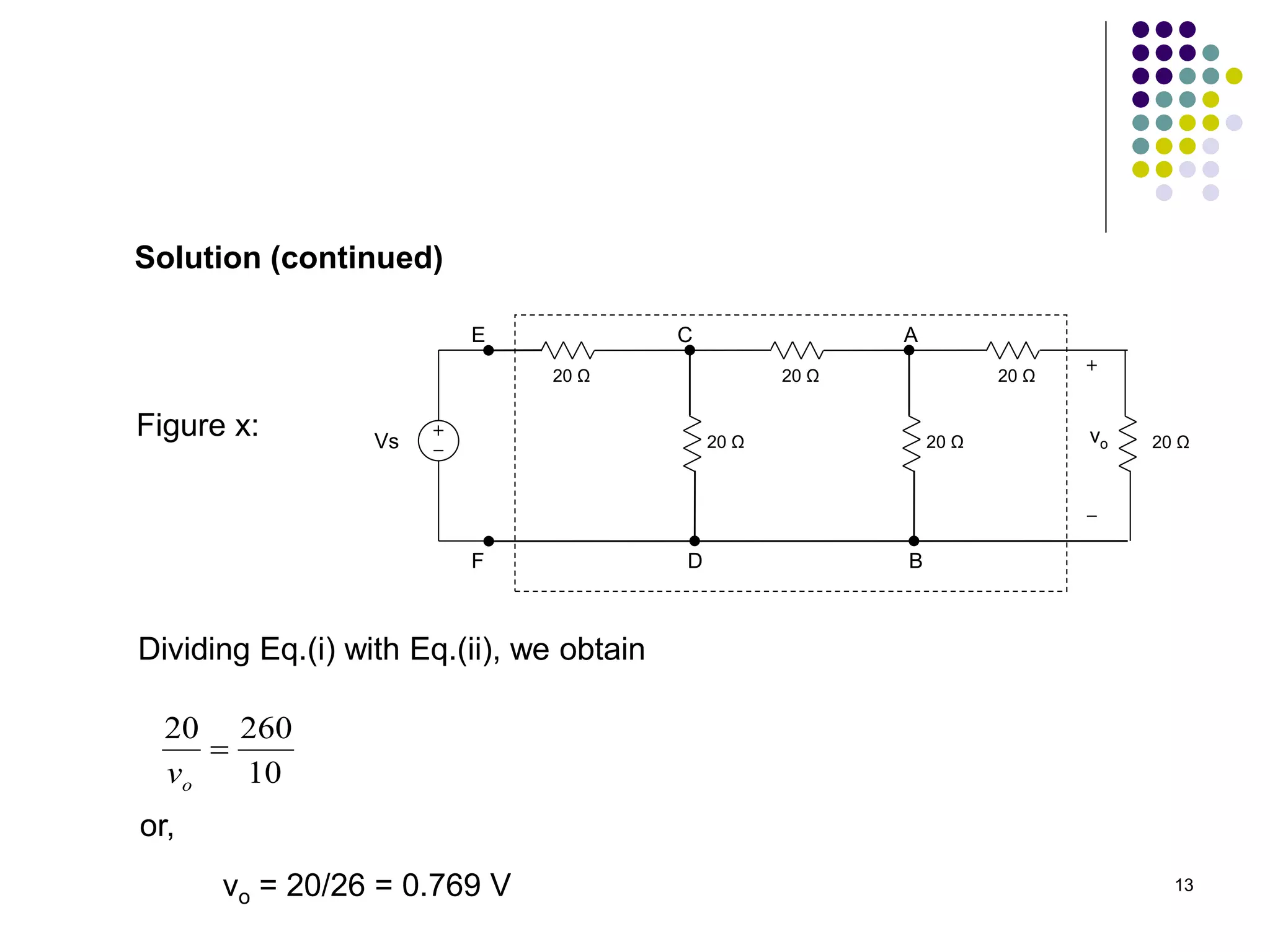
Figure x
[ Ans: vo = 3 V ]

15. 15
Superposition Theorem
Superposition Theorem
The superposition theorem is very useful for analysing a linear circuit with
more than one independent source. The superposition theorem helps ease
the solution of a complex circuit by doing away with the need to solve
simultaneous linear equations.
The overall response of a circuit containing several sources is the sum of
the responses to each individual source with the other sources killed.
Current sources are killed, or zeroed out, by replacing them with open circuits
and voltage sources by short circuits.
Note

16. 16
vs1
vs2
is1
R
io
vo
Linear
network
Consider a linear network where three linear sources are supplying power
to a linear resistor R, as shown in the figure below.

17. 17
To calculate the voltage vo and the current io due to the voltage source vs1,
we replace voltage source vs2 with a short-circuit and current source is1
with an open-circuit.
vs1
R
io1
vo1
Linear
network
Let vo1 be the voltage drop at resistor R due to the current flow
through it caused by voltage source VS1.

18. 18
To calculate the voltage vo and the current io due to the voltage source vs2,
we replace voltage source vs1 with a short-circuit and current source is1
with an open-circuit.
vs2 R
io2
vo2
Linear
network
Let vo2 be the voltage drop at resistor R due to the current flow
through it caused by voltage source VS2.

19. 19
To calculate the voltage vo and the current io due to the curent source is1,
we replace voltage sources vs1 and vs2 with short-circuits.
is1
R
io3
vo3
Linear
network By superposition theorem, we can write
vo = vo1 + vo2 + vo3
and
io = io1 + io2 + io3
Let vo3 be the voltage drop at resistor R
due to the current flow through it caused by
current source iS1.

20. 20
Superposition Theorem
Worked Example
Use superposition theorem to find the voltage v in the circuit shown in Figure x.
18 V
6 Ω
2 Ω 3 Ω
2 A
6 V
A
B
C
D
v

21. 21
Superposition Theorem
Solution
1. To find the voltage drop v1 due to the 6-V source only, we replace the 18-
V source with a short-circuit and the 2 A source with an open-circuit, as
shown in Figure x. To help us recognise which resistors are in parallel
and which are in series, the circuit in Figure x can be redrawn in the form
shown in Figure y.
6 Ω
2 Ω 3 Ω
6 V
A
B
C
D
v
6 Ω
6 V
A
C
B, D
v1
2 Ω 3 Ω

22. 22
Superposition Theorem
By voltage division, we have
Solution
V
4
6
3
2
6
2
6
3
1 





v
2. To find the voltage drop v2 due to the
18-V source, we replace the 6-V source
in Figure x with a short-circuit and the
2-A source with an open circuit. The
resulting circuit is shown in Figure x.
18 V
6 Ω
2 Ω 3 Ω
A
B
C
D
v2
Again, to help us identify which resistors
are in parallel and which are in series, the
circuit in Figure x is redrawn as shown in
Figure y.
18 V
6 Ω
2 Ω
A
C
D
3 Ω
B
v2

23. 23
Superposition Theorem
Solution (continued)
By voltage division, we have
V
3
18
6
2
3
2
3
2
3
2
3
2 







v
3. To find the voltage drop v3 due to the 2-
A current source, we replace the 6-V
and the 18-V sources in Figure x with
short-circuits. The resulting circuit is
shown in Figure x.
6 Ω
2 Ω 3 Ω
2 A
A
B
C
D
v3
The circuit in Figure x can be redrawn
as shown in Figure y.
6 Ω 2 Ω 3 Ω 2 A
A
C
D B
v3

24. 24
Superposition Theorem
Solution (continued)
The total resistance RT seen by the 2-A current source is given by
3
1
2
1
6
1
1



T
R
Hence, RT = 1 Ω and
v3 = - i x RT = - (2)(1) = - 2 V
The total output voltage due to the three sources is the sum of the
individual responses;
v = v1 + v2 +v3 = 4 + 3 + (-2) = 5 V

25. 25
Exercise
For the circuit shown below, use superposition principle to find i(t).
Take R = 1 Ω.