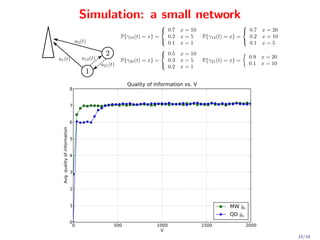
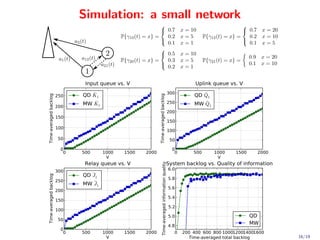
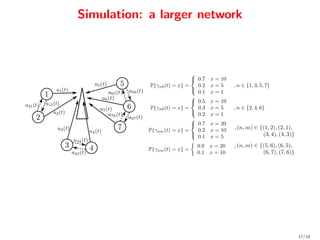
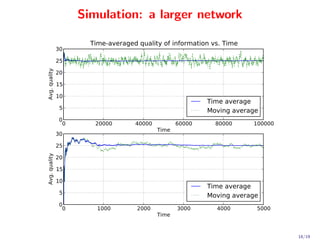
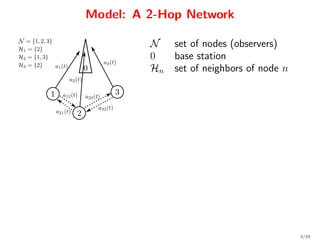
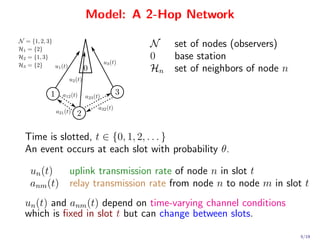
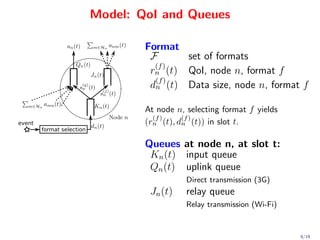
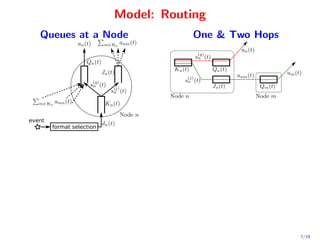
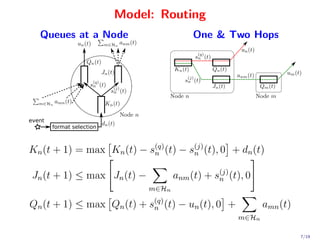
This document proposes a novel quadratic policy for maximizing quality of information (QoI) in a two-hop wireless network. It models a system where observers record random events in different formats, which have varying QoI values and data sizes. Data is transmitted over time-varying channels either directly or by relaying through neighbors, with a maximum of two hops. The policy formulates the problem using Lyapunov optimization to stabilize queues while maximizing average received QoI. It presents a quadratic formulation that yields separable subproblems allowing distributed implementation, improving over standard linearized approaches. Analysis shows average QoI achieves optimality within O(1/V) while average queue size grows within O(

1. Quality of Information Maximization
in Two-Hop Wireless Networks
Sucha Supittayapornpong, Michael J. Neely
IEEE ICC 2012
May 12, 2012
Electrical Engineering
University of Southern California

2. Motivation
Rate optimization problems and algorithms have long been
studied. (Chiang, 2007) (Neely, 2006)
However, application-layer utility, which affects directly to users, is
not considered.
2/19

3. Motivation
Rate optimization problems and algorithms have long been
studied. (Chiang, 2007) (Neely, 2006)
However, application-layer utility, which affects directly to users, is
not considered.
Quality of Information (QoI) is the usefulness of
information (Kang, 2010) (Johnson, 2005)
Its value depends on how valuable the information is to users.
The value is not necessarily proportional to a number of bits.
Example: QoI may depend on
- Formats (ex: video, audio, text),
- Quality (ex: resolution, simpling rate)
2/19

4. Motivation
Rate optimization problems and algorithms have long been
studied. (Chiang, 2007) (Neely, 2006)
However, application-layer utility, which affects directly to users, is
not considered.
Quality of Information (QoI) is the usefulness of
information (Kang, 2010) (Johnson, 2005)
Its value depends on how valuable the information is to users.
The value is not necessarily proportional to a number of bits.
Example: QoI may depend on
- Formats (ex: video, audio, text),
- Quality (ex: resolution, simpling rate)
A static system of QoI maximization was proposed by Liu
in 2011.
The system optimizes total quality of information obtained from an
event.
An integer programming was proposed.
2/19

5. A System in Consideration
A system consisting of observers maximizes average QoI
obtained from random events.
- This is a more general version of a previous static system (Liu,
2011)
3/19

6. A System in Consideration
A system consisting of observers maximizes average QoI
obtained from random events.
- This is a more general version of a previous static system (Liu,
2011)
Observers select a format to record an event.
Different formats have different QoI values
Always selecting highest quality format can overload a network.
implication: Intelligent format selection is needed.
3/19

7. A System in Consideration
A system consisting of observers maximizes average QoI
obtained from random events.
- This is a more general version of a previous static system (Liu,
2011)
Observers select a format to record an event.
Different formats have different QoI values
Always selecting highest quality format can overload a network.
implication: Intelligent format selection is needed.
Data is transmitted over time-varying channels to a base
station in two modes.
Direct transmission (3G)
Relay to neighbors (Wi-Fi)
in order to utilize better channels (3G) of neighbors
3/19

8. A System in Consideration
A system consisting of observers maximizes average QoI
obtained from random events.
- This is a more general version of a previous static system (Liu,
2011)
Observers select a format to record an event.
Different formats have different QoI values
Always selecting highest quality format can overload a network.
implication: Intelligent format selection is needed.
Data is transmitted over time-varying channels to a base
station in two modes.
Direct transmission (3G)
Relay to neighbors (Wi-Fi)
in order to utilize better channels (3G) of neighbors
Maximum of two hops is allowed to reduce queuing delay.
3/19

9. Contributions
A two-hop system maximizing QoI has been
modeled in such a way that
Randomness of events and transmission rates are
considered.
Loops in Routing are avoided.
The number of hops is at most 2 to reduce delay.
4/19

10. Contributions
A two-hop system maximizing QoI has been
modeled in such a way that
Randomness of events and transmission rates are
considered.
Loops in Routing are avoided.
The number of hops is at most 2 to reduce delay.
A novel quadratic policy has been proposed.
The policy reduces significant number of backlogs in
the system.
It can also be applied to the general Lyapunov
optimization technique.
4/19

11. Model: A 2-Hop Network
N set of nodes (observers)
0 base station
Hn set of neighbors of node n
5/19

12. Model: A 2-Hop Network
N set of nodes (observers)
0 base station
Hn set of neighbors of node n
Time is slotted, t ∈ {0, 1, 2, . . . }
An event occurs at each slot with probability θ.
5/19

13. Model: A 2-Hop Network
N set of nodes (observers)
0 base station
Hn set of neighbors of node n
Time is slotted, t ∈ {0, 1, 2, . . . }
An event occurs at each slot with probability θ.
un (t) uplink transmission rate of node n in slot t
anm (t) relay transmission rate from node n to node m in slot t
un (t) and anm (t) depend on time-varying channel conditions
which is fixed in slot t but can change between slots.
5/19

14. Model: QoI and Queues
Format
F set of formats
(f )
rn (t) QoI, node n, format f
(f )
dn (t) Data size, node n, format f
At node n, selecting format f yields
(f ) (f )
event (rn (t), dn (t)) in slot t.
format selection
6/19

15. Model: QoI and Queues
Format
F set of formats
(f )
rn (t) QoI, node n, format f
(f )
dn (t) Data size, node n, format f
At node n, selecting format f yields
(f ) (f )
event (rn (t), dn (t)) in slot t.
format selection
Queues at node n, at slot t:
Kn (t) input queue
Qn (t) uplink queue
Direct transmission (3G)
Jn (t) relay queue
Relay transmission (Wi-Fi)
6/19

16. Model: Routing
Queues at a Node One & Two Hops
event
format selection
7/19

17. Model: Routing
Queues at a Node One & Two Hops
event
format selection
Kn (t + 1) = max Kn (t) − s(q) (t) − s(j) (t), 0 + dn (t)
n n
Jn (t + 1) ≤ max Jn (t) − anm (t) + s(j) (t), 0
n
m∈Hn
Qn (t + 1) ≤ max Qn (t) + s(q) (t) − un (t), 0 +
n amn (t)
m∈Hn
7/19

18. Problem Formulation
Received QoI at time t
y0 (t) = rn (t)
n∈N
8/19

19. Problem Formulation
Received QoI at time t
y0 (t) = rn (t)
n∈N
Optimization problem:
t−1
1
max lim E {y0 (τ )}
t→∞ t
τ =0
s. t. all queues Kn (t), Qn (t), Jn (t) are mean rate stable
This problem is solved by the Lyapunov optimization.
(Neely, 2010)
8/19

20. Lyapunov Optimization Technique
Lyapunov function (Tassiulas, 1992) :
1
L(t) Kn (t) + Q2 (t) + Jn (t)
2
n
2
2 n∈N
- All queue lengths at time t are cast to a 1-dim value.
9/19

21. Lyapunov Optimization Technique
Lyapunov function (Tassiulas, 1992) :
1
L(t) Kn (t) + Q2 (t) + Jn (t)
2
n
2
2 n∈N
- All queue lengths at time t are cast to a 1-dim value.
Lyapunov drift: ∆(t) L(t + 1) − L(t)
- The drift represents the difference of queues in consecutive slots.
- Minimizing the drift lead to mean rate stability of all queues.
9/19

22. Lyapunov Optimization Technique
Lyapunov function (Tassiulas, 1992) :
1
L(t) Kn (t) + Q2 (t) + Jn (t)
2
n
2
2 n∈N
- All queue lengths at time t are cast to a 1-dim value.
Lyapunov drift: ∆(t) L(t + 1) − L(t)
- The drift represents the difference of queues in consecutive slots.
- Minimizing the drift lead to mean rate stability of all queues.
Drift-plus-penalty function with variable V (Neely, 2010)
∆(t) + V (−y0 (t))
where −y0 (t) is a penalty value at time t.
- Minimizing this function every slot will stabilize queues and
optimize the objective function.
9/19

23. Lyapunov Drift Minimization
Pure Lyapunov optimization has quadratic nature of ∆(t).
1 2
min (max[Q(t) − b(t), 0] + a(t)) − Q2 (t)
a(t),b(t) 2
Reduce delay, Non-separable decisions (centralized algorithm)
10/19

24. Lyapunov Drift Minimization
Pure Lyapunov optimization has quadratic nature of ∆(t).
1 2
min (max[Q(t) − b(t), 0] + a(t)) − Q2 (t)
a(t),b(t) 2
Reduce delay, Non-separable decisions (centralized algorithm)
Standard Lyapunov optimization optimizes a linearized ∆(t).
min Q(t) [a(t) − b(t)] (T assiulas, 1992)(N eely, 2010)
a(t),b(t)
Large delay, Separable decisions (distributed algorithm)
10/19

25. Lyapunov Drift Minimization
Pure Lyapunov optimization has quadratic nature of ∆(t).
1 2
min (max[Q(t) − b(t), 0] + a(t)) − Q2 (t)
a(t),b(t) 2
Reduce delay, Non-separable decisions (centralized algorithm)
Standard Lyapunov optimization optimizes a linearized ∆(t).
min Q(t) [a(t) − b(t)] (T assiulas, 1992)(N eely, 2010)
a(t),b(t)
Large delay, Separable decisions (distributed algorithm)
Novel Quadratic Lyapunov Optimization preserves the quadratic
nature of ∆(t).
2 2
min [Q(t) + a(t)] + [Q(t) − b(t)]
a(t),b(t)
Reduce delay, Separable decisions (distributed algorithm)
10/19

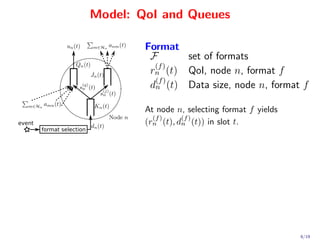
26. Quadratic Policy
min
2 2
 
 K (t) − s(q) (t) + K (t) − s(j) (t) +
n n


 n n 

 
 2 
(q)
[Kn (t) + dn (t)]2 + [Qn (t) − un (t)]2 + Qn (t) + sn (t) +

 

2 2
n∈N  Qn (t) +

 m∈Hn amn (t) + Jn (t) − m∈Hn anm (t) + 


 2 
 Jn (t) + s(j) (t) − 2V rn (t)

 

n

s. t.
s(q) (t) ∈ {0, 1, 2, . . . , s(q)(max) }, s(j) (t) ∈ {0, 1, 2, . . . , s(j)(max) } ,
n n n n
fn (t) ∈ F, dn (t) = d(fn (t)) (t), rn (t) = rn n (t)) (t) , n ∈ N
n
(f
a(t) ∈ Aγ(t) , u(t) ∈ Uγ(t)
11/19

27. Separable Problems (1)
Admission-Control problem:
2
min Kn (t) + d(fn (t)) (t)
n − 2V rn n (t)) (t)
(f
fn (t)∈F
Uplink-Routing problem:
2 2
min Kn (t) − s(q) (t)
n + Qn (t) + s(q) (t)
n
(q) (q)(max)
sn (t)∈{0,1,...,sn }
Relay-Routing problem:
2 2
min Kn (t) − s(j) (t)
n + Jn (t) + s(j) (t)
n
(j) (j)(max)
sn (t)∈{0,1,...,sn }
12/19

28. Separable Problems (2)
Uplink-Allocation problem:
min [Qn (t) − un (t)]2
u(t)∈Uγ(t)
n∈N
Relay-Allocation problem:
2 2
min Qn (t) − amn (t) + Jn (t) − anm (t)
a(t)∈Aγ(t)
n∈N m∈Hn m∈Hn
13/19

29. Performance Bounds
QoI vs. V
The avg. QoI approaches optimality with O(1/V )
t−1
1 A (opt)
lim inf E {y0 (τ )} ≥ − + y0
t→∞ t V
τ =0
14/19

30. Performance Bounds
QoI vs. V
The avg. QoI approaches optimality with O(1/V )
t−1
1 A (opt)
lim inf E {y0 (τ )} ≥ − + y0
t→∞ t V
τ =0
Total queue backlog vs. V
The avg. queue size grows with order O(V )
t−1
1
lim sup E {Kn (τ ) + Qn (τ ) + Jn (τ )}
t→∞ t τ =0 n∈N
A V (max) ( )
≤ + y0 − y0
14/19

31. Simulation: a small network
Quality of Information vs. V
8
7
6
Avg. quality of information
5
4
3
2
1 MW y0
¯
QD y0
¯
00 500 1000 1500 2000
V
15/19

32. Simulation: a small network
Input queue vs. V Uplink queue vs. V
250 QD K1
¯ 300 QD Q1
¯
Time-averaged backlog
Time-averaged backlog
MW K1¯ 250 MW Q1¯
200
200
150
150
100 100
50 50
00 500 1000 1500 2000 00 500 1000 1500 2000
V V
Relay queue vs. V System backlog vs. Quality of information
Time-averaged information quality
300 6.0
QD J1
¯
5.8
Time-averaged backlog
250 MW J1
¯
200 5.6
150 5.4
100 5.2
50 5.0 QD
4.8 MW
00 500 1000 1500 2000 0 200 400 600 800 1000120014001600
V Time-averaged total backlog 16/19

33. Simulation: a larger network
17/19

34. Simulation: a larger network
Time-averaged quality of information vs. Time
30
25
20
Avg. quality
15
10
Time average
5 Moving average
00 20000 40000 60000 80000 100000
30 Time
25
20
Avg. quality
15
10
Time average
5 Moving average
00 1000 2000 3000 4000 5000
Time
18/19

35. Conclusion
We have formulated a more realistic QoI maximization
system.
We have proposed the novel Quadratic Lyapunov
Optimization technique.
The technique reduces significantly numbers of backlogs.
The technique is general for Lyapunov Optimization technique.
We have derived the distributed algorithm which
approaches optimality.
19/19