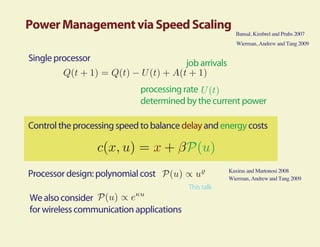
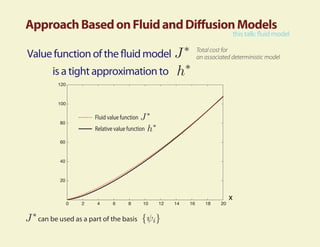
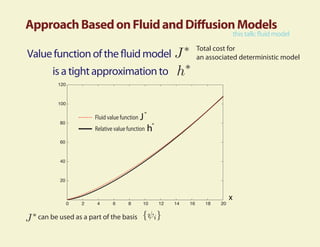
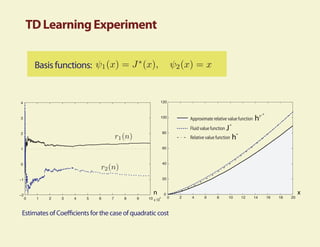
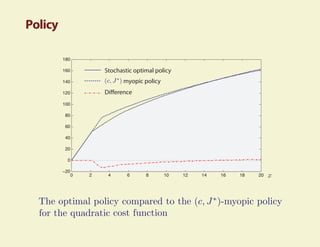
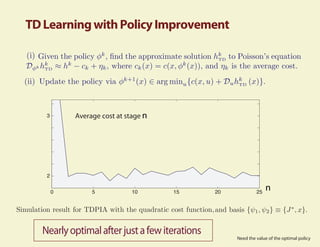
This document summarizes research on using fluid and diffusion approximations within approximate dynamic programming for applications in power management. Specifically, it discusses how: 1) The fluid value function provides a tight approximation to the relative value function and can be used as part of the basis for TD learning. 2) TD learning with policy improvement finds a near-optimal policy in a few iterations when applied to power management problems. 3) Fluid and diffusion models provide useful insights into the structure of optimal policies for average cost problems.

1. Approximate Dynamic Programming using
Fluid and Diffusion Approximations
with Applications to Power Management
Speaker: Dayu Huang
Wei Chen, Dayu Huang, Ankur A. Kulkarni,1Jayakrishnan Unnikrishnan, Quanyan Zhu,
Prashant Mehta, Sean Meyn, and Adam Wierman 2
Coordinated Science Laboratory, UIUC
Dept. of IESE, UIUC 1
Dept. of CS, California Inst. of Tech. 2
4 120
3 100
80
J
2
1 60
National Science Foundation (ECS-0523620 and CCF-0830511), 0 40
ITMANET DARPA RK 2006-07284, and Microsoft Research
−1 20
−2 n 0 x
0 1 2 3 4 5 6 7 8 9 10 x 104 0 2 4 6 8 10 12 14 16 18 20

2. Introduction
MDP model Control
i.i.d
Cost
Minimize average cost

3. Introduction
MDP model Control
i.i.d
Cost
Minimize average cost
Generator

4. Introduction
MDP model Control
i.i.d
Cost
Minimize average cost
Average Cost Optimality Equation (ACOE)
Generator
Relative value function
Solve ACOE and Find

5. TD Learning
The “curse of dimensionality”:
Complexity of solving ACOE grows exponentially with
the dimension of the state space.
Approximate within a nite-dimensional function class
Criterion: minimize the mean-squre error
solved by stochastic approximation algorithms

6. TD Learning
The “curse of dimensionality”:
Complexity of solving ACOE grows exponentially with
the dimension of the state space.
Approximate within a nite-dimensional function class
Criterion: minimize the mean-squre error
solved by stochastic approximation algorithms
Problem: How to select the basis functions ?
key to the success of TD learning

7. Total cost for
an associated deterministic model
is a tight approximation to
120
100
Fluid value function
80
Relative value function
60
40
20
0 2 4 6 8 10 12 14 16 18 20
can be used as a part of the basis

8. Related Work
Multiclass queueing network
Meyn 1997, Meyn 1997b
optimal control Chen and Meyn 1999
simulation Hendersen et.al. 2003
network scheduling Veatch 2004
and routing Moallemi, Kumar and Van Roy 2006
Meyn 2007 Control Techniques for
Complex Networks
other approaches Tsitsiklis and Van Roy 1997
Mannor, Menache and Shimkin 2005

9. Related Work
Multiclass queueing network
Meyn 1997, Meyn 1997b
optimal control Chen and Meyn 1999
simulation Hendersen et.al. 2003
network scheduling Veatch 2004
and routing Moallemi, Kumar and Van Roy 2006
Meyn 2007 Control Techniques for
Complex Networks
other approaches Tsitsiklis and Van Roy 1997
Mannor, Menache and Shimkin 2005
Taylor series approximation this work

10. Power Management via Speed Scaling
Bansal, Kimbrel and Pruhs 2007
Wierman, Andrew and Tang 2009
Single processor
job arrivals
processing rate
determined by the current power
Control the processing speed to balance delay and energy costs
Kaxiras and Martonosi 2008
Processor design: polynomial cost Wierman, Andrew and Tang 2009
This talk
We also consider
for wireless communication applications

11. Fluid Model MDP
Fluid model:
Total Cost
Total Cost Optimality Equation (TCOE) for the uid model:

12. Why Fluid Model? MDP
First order Taylor series approximation

13. Why Fluid Model? MDP
First order Taylor series approximation
TCOE
ACOE
almost solves the ACOE Simple but
powerful idea!

14. Policy
180
160 Stochastic optimal policy
140 myopic policy
120 Di erence
100
80
60
40
20
0
−20
0 2 4 6 8 10 12 14 16 18 20 x

15. Value Iteration
250
200
150 Initialization: V0 0
Initialization: V0 =
100
50
0
5 10 15 20 n
(See also [Chen and Meyn 1999])

16. Approximation of the Cost Function
Error Analysis
constant?

17. Approximation of the Cost Function
Error Analysis
constant?
Surrogate cost
approximates
Bounds on ?

18. Structure Results on the Fluid Solution

19. Lower Bound
Convexity of

20. Lower Bound
Convexity of

21. Upper Bound

22. Upper Bound

23. Upper Bound

24. Approach Based on Fluid and Di usion Models
this talk: uid model
Total cost for
Value function of the uid model an associated deterministic model
is a tight approximation to
120
100
Fluid value function
80
Relative value function
60
40
20
0 2 4 6 8 10 12 14 16 18 20
can be used as a part of the basis

25. TD Learning Experiment
Basis functions:
4 120
3 100 Approximate relative value function
Fluid value function
2 80
Relative value function
1 60
0 40
−1 20
−2 0
0 1 2 3 4 5 6 7 8 9 10 x 104 0 2 4 6 8 10 12 14 16 18 20
Estimates of Coe cients for the case of quadratic cost

26. TD Learning with Policy Improvement
3 Average cost at stage
2
0 5 10 15 20 25
Nearly optimal after just a few iterations
Need the value of the optimal policy

27. Conclusions
The uid value function can be used as a part of the basis for TD-learning.
Motivated by analysis using Taylor series expansion:
The uid value function almost solves ACOE. In particular,
it solves the ACOE for a slightly di erent cost function; and
the error term can be estimated.
TD learning with policy improvement gives a near optimal policy
in a few iterations, as shown by experiments.
Application in power management for processors.

28. References
[1] W. Chen, D. Huang, A. Kulkarni, J. Unnikrishnan, Q. Zhu, P. Mehta, S. Meyn, and A. Wierman.
Approximate dynamic programming using fluid and diffusion approximations with applications to power
management. Accepted for inclusion in the 48th IEEE Conference on Decision and Control, December
16-18 2009.
[1] P. Mehta and S. Meyn. Q-learning and Pontryagin’s Minimum Principle. To appear in Proceedings of
the 48th IEEE Conference on Decision and Control, December 16-18 2009.
[1] R.-R. Chen and S. P. Meyn. Value iteration and optimization of multiclass queueing networks. Queueing
Syst. Theory Appl., 32(1-3):65–97, 1999.
[1] S. G. Henderson, S. P. Meyn, and V. B. Tadi´. Performance evaluation and policy selection in multiclass
c
networks. Discrete Event Dynamic Systems: Theory and Applications, 13(1-2):149–189, 2003. Special
issue on learning, optimization and decision making (invited).
[1] S. P. Meyn. The policy iteration algorithm for average reward Markov decision processes with general
state space. IEEE Trans. Automat. Control, 42(12):1663–1680, 1997.
[1] S. P. Meyn. Control Techniques for Complex Networks. Cambridge University Press, Cambridge, 2007.
[1] C. Moallemi, S. Kumar, and B. Van Roy. Approximate and data-driven dynamic programming for
queueing networks. Preprint available at http://moallemi.com/ciamac/research-interests.php, 2008.