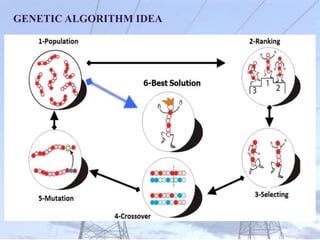
This document summarizes a thesis on using genetic algorithms to optimize space trusses. It begins with background information on the thesis author and supervisors. It then discusses the importance of structural optimization to reduce weight while maintaining safety. The research objectives are outlined as developing a new approach to overcome drawbacks of classical optimization methods by using different design variables. The document provides details on the genetic algorithm approach and compares the proposed method to traditional techniques. Several case studies are presented to demonstrate applying the proposed approach to optimize benchmark space truss problems. Results are compared to other studies to validate the effectiveness of the method.

1. ZAGAZIG UNIVERSITY
FACULTY OF ENGINEERING
STRUCTURAL ENGINEERING DEPARTMENT
Optimization of Space Trusses Using Genetic
Algorithm
By
Osman Hamdy Osman Mohammed
B.Sc. in Civil Engineering, Faculty of Engineering, Zagazig University
Supervised by
Prof. Dr. Osman Shallan
Prof. of Structural Engineering - Head of Structural Engineering Department - Zagazig University
Prof. Dr. Atef Eraky
Prof. of Structural Engineering - Zagazig University
2015
Asst. Prof. Dr. Tharwat Sakr
Asst. Prof. of Structural Engineering - Zagazig University

2. 2
Optimization is a design process aims to save the
most valuable factors used where in structure
case it is the weight and that leads to safe :
STRUCTURAL OPTIMIZATION IMPORTANCE

3. 3
Truss optimization
categories
Shape
optimization
Topology
optimization
TRUSS OPTIMIZATION CATEGORIES

4. The objective of this research is to develop a new approach to overcome drawbacks
of classical method by using untraditional variables
Study
objectives
Reduce No
of variables
and
chromosome
Length
Overcome
drawbacks
of using X-
section as a
variable
Over come
complexity of
making
Topology Opt.
simultaneousl
y With other
Opts.
THE OBJECTIVE OF THIS RESEARCH

5. GENETIC ALGORITHM
Genetic algorithm (GA) is an optimization tool that mimics the processes
of evolution theory through selection , crossover and mutation processes.
.
For instance, the following string consists of five genes, g1-g5, representing five design variables:
𝑁𝑜. 𝑜𝑓 𝐵𝑖𝑡𝑒𝑠 = 𝑙𝑜𝑔2
ximax
− ximin
∈ i
Where:
Xi
min is the lower bound of variable i;
Xi
max is the upper bound of variable i;
∈i is the desired precision in variable i;
In GA decimal values represented in binary coded string
The number of string (chromosome ) bites is dependent on
The number
of variables
need opt.
Min. and Max
limits for the
variable.
The required
precision.
No of object
subjected To
opt.

6. GENETIC ALGORITHM IDEA

7. 7
Design Variables in Traditional
Technique
Members
cross sections
A1,A2,A3 …etc.
Shape
optimization
Free nodes
coordinates
x1,y1,z1,x2,y2,z2
…etc.
Topology
optimization
Members
distribution
1 for presence
0 for absence
TRADITIONAL VARIABLE

8. Design Variables in proposed approach
Nodal coordinates x, y and z
coordinates of variable nodes of the
truss
Nodal Deflection Dx, Dy and Dz
of non-support nodes of the truss
Chromosome sample for 10-bar plane truss
PROPOSED APPROACH VARIABLES

9. COMPARISONS BETWEEN NO. OF BITES FOR TRADITIONALAND
PROPOSED APPROACH
10-bar plane benchmark truss.
Optimization Variable Traditional Method Proposed Method
Shape 30 30
Size 80 ‫ــــــــــــــــــــــــــ‬
Topology 10 ‫ــــــــــــــــــــــــــ‬
Deflection ‫ــــــــــــــــــــــــــ‬ 48
Total 120 Bites 78 Bites
No. of possible solutions 1.32923E+36 3.02231E+23
As it is shown the number of possible solution has been reduced from
1.32923E+36 to 2.8823E+17 which represents approximately 100 % reduction.

10. 10
Proposed Versus
Traditional Approaches
X-sec. Random
Selection
X-sec. Long
Chromosome
Topology
complex.
Shorter
Chromosome
Reduction In No. of Variables
Defl. Limit is Lower than X-sec. limits
Defl. Related to nodes not members
Defl. Limits could be reduced 50%
Better
Solution
TRADITIONAL VARIABLE

11. Proposed Steps
Calculate each member length in the truss according to
proposed coordinates Li = ∆x2 + ∆y2 + ∆z 2
Calculate each member elongation according to proposed
deflections and coordinates
ΔL = ∆x Cosθx + ∆y Cosθy + ∆z Cosθz
Combining topology matrix by comparing the strain of each
member to the allowable strain of used material (all)
excluding members violate this condition
0.0 <
𝛥𝐿
L0
≤ εall
Making analysis for the proposed truss (topology and node
coordinate) considering A/L=constant to check the stability
and to get the local forces Fi in the truss members
Calculate the proposed cross section for each member Ai
= Max(
Fi
σall
,
FiLi
E∆Li
)
Finally making full analysis for the proposed truss (topology,
node coordinates and member cross sections ) to check stress
and deflection constrains

12. constraints
Stability
The proposed
truss must be
statically
stable
Constructability
No nodes
come over
other one
Member
stresses
All members
stresses not
exceed
allowable
stress
Nodal
displacements
All nodes
deflections
not exceed
allowable
deflection

13. Proposed approach is used to optimize the most
three famous benchmark problems through the
literature
25-bar space
truss
72-bar space
truss
STUDY CASES

14. A- SIZE, SHAPE AND TOPOLOGY OPTIMIZATION FOR 10-BAR PLANE TRUSS .
F=445.374 KN (100 kips) & a=9.144 m (360 inches) , E = 68.95 Gpa (104 ksi) & ρ = 2
,768 kg/m3 (0.1 lb/in3) allowable stress=172.37 MPa (25 KSI) & allowable deflection =
50.8 mm (in2).
Structure of the10-bar truss

15. Optimized structure of the 10-bar
The optimized truss consist of 6-bars and 5-nodes where 4 bars are
removed. Coordinates of free Node P3 is (11.73 ; 6.4).
A- SIZE, SHAPE AND TOPOLOGY OPTIMIZATION FOR 10-BAR PLANE TRUSS .
Max. actual deflection absolute value is 50.79 in Z- direction at node P2
which represent 99.98% of allowable deflection
Max. actual stress absolute value is 23.424 KSI at member M1 which
represents 93.70% of allowable stress
Element No.
Area
in2
m2
M1 6.045 0.004
M2 24.18 0.016
M3 19.18 0.012
M4 12.5 0.008
M5 21.08 0.014
M6 28.87 0.019
Cross Sections Area

16. Results of 10-bar plane truss compared with literature results.
Search Method
Optimization category
Weight (lbs.) Note
Size Shape Topology
Rajeev (1992) LINRM √
6249.00
Rajeev (1992) SUMT √
5932.00
Rajeev (1992) GRP-UI √
5727.00
Rajeev (1992) M-5 √
5725.00
Rajeev (1992) M-3 √
5719.00
Rajeev (1992) Genetic algorithm √
5613.84
Coello Coello (1994) Genetic algorithm √
5586.59
Rajeev (1992) CONMIN √
5563.00
Rajeev (1992) OPTDYN √
5472.00
Galante (1996) Genetic algorithm √ √ 5119.3
Kripakaran, Gupta and Baugh Jr. (2007) Hybrid search method. √ 5073.03
Li, Huang and Liu (2006) Particle swarm √ 5060.9
Su Ruiyi, Gui Liangjin, Fan Zijie (2009) Genetic algorithm √ √ 4962.07
Schmid (1997) Genetic algorithm √ √ 4962.10
Rajan (1995) Genetic algorithm √ √ 4962.1
Hajela and Lee (1995) Genetic algorithm √ √ 4942.7
Rajeev (1997) Genetic algorithm √ √ √ 4925.80 Two stages
Wenyan (2005) Genetic algorithm √ √ 4921.25
Deb and Gulati (2001) Genetic algorithm √ √ 4899.15
H. Rahami, A. Kaveh (2008) Force method √ √ 4855.2
Deb and Gulati (2001)
Genetic algorithm √ √ 4731.65
Const. constrain
not considered
Genetic algorithm √ √ 4899.15
Const. constrain
considered
This study Genetic algorithm √ √ √ 4762.1
A- SIZE, SHAPE AND TOPOLOGY OPTIMIZATION FOR 10-BAR PLANE TRUSS .

17. B- SIZE OPTIMIZATION FOR 25-BAR SPACE TRUSS.
E =68.95 GPa (104 ksi) & ρ = 2,768 kg/m3 (0.1 lb/in3) allowable stress= 275.8 MPa (40
KSI) & allowable deflection = 8.9 mm (0.35 in).
Structure of 25-bar truss
Node Fx (lbs.) Fy (lbs.) Fz (lbs.)
1 1000 -10000 -10000
2 0 -10000 -10000
3 500 0 0
6 600 0 0
Loading case

18. Member Area (in2) Length (in) Weight (lb.)
1,2 0.1 75.00 0.75
2,6 0.3 130.50 3.92
1,5 0.3 130.50 3.92
2,3 0.3 130.50 3.92
1,4 0.3 130.50 3.92
1,6 3.6 106.80 38.45
1,3 3.6 106.80 38.45
2,5 3.6 106.80 38.45
2,4 3.6 106.80 38.45
6,5 1.7 75.00 12.75
3,4 1.7 75.00 12.75
5,4 0.1 75.00 0.75
6,3 0.1 75.00 0.75
4,9 0.8 181.14 14.49
5,8 0.8 181.14 14.49
6,7 0.8 181.14 14.49
3,10 0.8 181.14 14.49
6,9 0.4 181.14 7.25
5,10 0.4 181.14 7.25
4,7 0.4 181.14 7.25
3,8 0.4 181.14 7.25
5,9 3.6 133.46 48.05
6,10 3.6 133.46 48.05
4,8 3.6 133.46 48.05
3,7 3.6 133.46 48.05
Weight (lb.) 476.337
Max. actual deflection absolute value is 8.8002
mm at node 1 in Y direction which represents
98.87% of allowable deflection.
Max. actual stress absolute value is 124.17
MPA (18.01 KSI) in member 6,3 which
represents 45.02% of allowable stress.
B- SIZE OPTIMIZATION FOR 25-BAR SPACE TRUSS.
Resulted Cross section for 25-bar space truss

19. Results of sizing optimized 25-bar space truss compared with literature results.
Search Year Weight (lbs.)
Zhu 1986 562.93
Rajeev and Krishnamoor-thy 1992 546.01
Coello et al. 1994 493.94
Cao 1996 485.05
Erbatur et al. 2000 493.8
Lee et al. 2005 484.85
Camp 2007 484.85
Kaveh and Shojaee 2007 484.85
To˘gan and Dalo˘glu 2008 483.35
Talaslioglu 2009 485.9
Li et al. 2009 484.85
Tayfun Dede 2011 484.85
This study 476.337
B- SIZE OPTIMIZATION FOR 25-BAR SPACE TRUSS.

20. Shape, Sizing and Topology optimized 25-bar space truss
structure Model in Matlab .
Size, shape and topology optimized 25-bar space
truss literature results
Members and its groups
Wu [48] Wenyan [22] H. Rahami [23]
This study
1995 2005 2008
Cross section area (in2)
1,2 Group 1 0.1 Removed Removed Removed
2,6
Group 2
0.2 0.10 0.10 0.10
1,5 0.2 0.10 0.10 0.10
2,3 0.2 0.10 0.10 0.10
1,4 0.2 0.10 0.10 Removed
1,6
Group 3
1.1 0.90 0.90 0.90
1,3 1.1 0.90 0.90 0.90
2,5 1.1 0.90 0.90 0.90
2,4 1.1 0.90 0.90 0.90
6,5
Group 4
0.2 Removed Removed Removed
3,4 0.2 Removed Removed Removed
5,4
Group 5
0.3 Removed Removed Removed
6,3 0.3 Removed Removed Removed
4,9
Group 6
0.10 0.10 0.10 0.10
5,8 0.10 0.10 0.10 0.10
6,7 0.10 0.10 0.10 0.10
3,10 0.10 0.10 0.10 0.10
6,9
Group 7
0.2 0.10 0.10 0.10
5,10 0.2 0.10 0.10 0.10
4,7 0.2 0.10 0.10 0.10
3,8 0.2 0.10 0.10 0.10
5,9
Group 8
0.90 1.00 1.00 1.00
6,10 0.90 1.00 1.00 1.00
4,8 0.90 1.00 1.00 1.00
3,7 0.90 1.00 1.00 1.00
X4 41.07 39.91 38.7913 40.60
Y4 53.47 61.99 66.111 58.40
Z4 124.6 118.23 112.9787 123.80
X8 50.8 53.13 48.7924 56.20
Y8 131.48 138.49 138.891 139.20
Weight (lb.) 136.2 114.74 114.3701 114.171
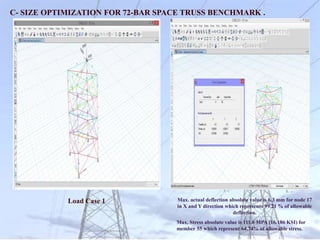
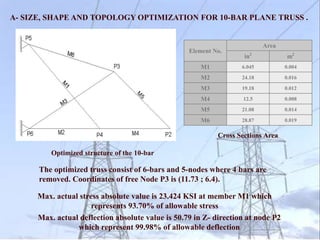
C- SIZE, SHAPE AND TOPOLOGY OPTIMIZATION FOR 25-BAR SPACE TRUSS.
Max. actual deflection absolute value is 8.8889 mm at node
1 in Y direction which represents 99.87% of allowable
deflection.
Max. actual stress absolute value is 119.62 MPA (17.35 KSI)
in member 2,5 which represents 43.73% of allowable stress .
Node 3,4,5& 6 are free in X,Y & Z Dir.
Node 7,8,9&10 are free in X& Y Dir.

21. C- SIZE OPTIMIZATION FOR 72-BAR SPACE TRUSS BENCHMARK .
E = 68.95 Gpa (104 ksi) & ρ = 2 ,768 kg/m3 (0.1 lb/in3) & allowable stress=172.37
MPa (25 KSI) & allowable deflection = 6.35 mm (0.25 in). in x and y directions for
nodes = 17,18,19 and 20.
Structure of the 72-bar truss

22. C- SIZE OPTIMIZATION FOR 72-BAR SPACE TRUSS BENCHMARK .
Member No. X-section group X-section Area (in2) Length (in) Weight (Lb) Member No. X-section group X-section Area (in2) Length (in) Weight (Lb)
1 A1 1.9941 60 11.96 37 A9 0.70363 60 4.22
2 A1 1.9941 60 11.96 38 A9 0.70363 60 4.22
3 A1 1.9941 60 11.96 39 A9 0.70363 60 4.22
4 A1 1.9941 60 11.96 40 A9 0.70363 60 4.22
5 A2 0.57611 134.16 7.73 41 A10 0.45689 134.16 6.13
6 A2 0.57611 134.16 7.73 42 A10 0.45689 134.16 6.13
7 A2 0.57611 134.16 7.73 43 A10 0.45689 134.16 6.13
8 A2 0.57611 134.16 7.73 44 A10 0.45689 134.16 6.13
9 A2 0.57611 134.16 7.73 45 A10 0.45689 134.16 6.13
10 A2 0.57611 134.16 7.73 46 A10 0.45689 134.16 6.13
11 A2 0.57611 134.16 7.73 47 A10 0.45689 134.16 6.13
12 A2 0.57611 134.16 7.73 48 A10 0.45689 134.16 6.13
13 A3 0.06734 120 0.81 49 A11 0.034095 120 0.41
14 A3 0.06734 120 0.81 50 A11 0.034095 120 0.41
15 A3 0.06734 120 0.81 51 A11 0.034095 120 0.41
16 A3 0.06734 120 0.81 52 A11 0.034095 120 0.41
17 A4 0.022226 169.71 0.38 53 A12 0.064083 169.71 1.09
18 A4 0.022226 169.71 0.38 54 A12 0.064083 169.71 1.09
19 A5 1.5916 60 9.55 55 A13 0.1733 60 1.04
20 A5 1.5916 60 9.55 56 A13 0.1733 60 1.04
21 A5 1.5916 60 9.55 57 A13 0.1733 60 1.04
22 A5 1.5916 60 9.55 58 A13 0.1733 60 1.04
23 A6 0.5536 134.16 7.43 59 A14 0.48978 134.16 6.57
24 A6 0.5536 134.16 7.43 60 A14 0.48978 134.16 6.57
25 A6 0.5536 134.16 7.43 61 A14 0.48978 134.16 6.57
26 A6 0.5536 134.16 7.43 62 A14 0.48978 134.16 6.57
27 A6 0.5536 134.16 7.43 63 A14 0.48978 134.16 6.57
28 A6 0.5536 134.16 7.43 64 A14 0.48978 134.16 6.57
29 A6 0.5536 134.16 7.43 65 A14 0.48978 134.16 6.57
30 A6 0.5536 134.16 7.43 66 A14 0.48978 134.16 6.57
31 A7 0.029919 120 0.36 67 A15 0.38727 120 4.65
32 A7 0.029919 120 0.36 68 A15 0.38727 120 4.65
33 A7 0.029919 120 0.36 69 A15 0.38727 120 4.65
34 A7 0.029919 120 0.36 70 A15 0.38727 120 4.65
35 A8 0.03593 169.71 0.61 71 A16 0.49385 169.71 8.38
36 A8 0.03593 169.71 0.61 72 A16 0.49385 169.71 8.38
Total Weight (Lb) 375.77
Resulted Cross section for 72-bar space truss

23. Load Case 1 Max. actual deflection absolute value is 6.3 mm for node 17
in X and Y direction which represents 99.21 % of allowable
deflection.
Max. Stress absolute value is 111.6 MPA (16.186 KSI) for
member 55 which represent 64.74% of allowable stress.
C- SIZE OPTIMIZATION FOR 72-BAR SPACE TRUSS BENCHMARK .

24. Load case 2 Max. Stress absolute value is 4.206/0.1733 = 24.27 KSI for
members 55, 56, 57 and 58 which represent 97.08% of
allowable stress.
Max. Stress absolute value is 0.99949 mm for nodes 17, 18, 19
and 20 in X and Y directions which represents 15.74 % of
allowable deflection.
C- SIZE OPTIMIZATION FOR 72-BAR SPACE TRUSS BENCHMARK .

25. 25
Size optimization results for 72-bar space truss.
Search Year W (lb)
Venkayya 1971 381.2
Gellatly and Berke 1971 395.97
Schmit and Farshi 1974 388.63
Khan et al. 1979 387.67
Adeli and Kamal 1986 379.31
Cao 1996 380.32
Erbatur et al. 2000 383.12
Barbaso and Lemonge 2003 384.1341
Camp 2007 379.85
Perez and Behdinan 2007 381.91
Talaslioglu 2009 380.783
Tayfun Dede 2011 382.35
This study 375.77
C- SIZE OPTIMIZATION FOR 72-BAR SPACE TRUSS BENCHMARK .

26. 26
Conclusion
Genetic algorithm
is considered as
suitable tool for
truss optimization.
The proposed
approach
succeeded to
reduce the
chromosome
length lead to
reduction in
calculation time
and effort.
Proposed
approach
succeeded to
overcome
traditional
drawbacks of x-
section variables
and topology
optimization
The results
obtained by using
the proposed
approach are
more optimized
when compared
with previous
research.

28. Max. actual deflection absolute value is 50.79 in Z- direction at node P2 which
represent 99.98% of allowable deflection
Element No. Dimensions (mm)
Area Stress
% Stress of allowable
in2 m2 KSI Mpa
M1 200x200x5 6.045 0.004 23.424 161.5 93.70%
M2 400x400x10 24.18 0.016 -8.398 -57.9 33.60%
M3 260x260x12.5 19.18 0.012 -5.782 -39.9 23.10%
M4 180x180x12 12.5 0.008 -8.236 -56.8 32.90%
M5 350x350x10 21.08 0.014 6.8122 46.97 27.20%
M6 400x400x12 28.87 0.019 7.1245 49.12 28.50%
Max. actual stress absolute value is 23.424 KSI at member M1 which represents
93.70% of allowable stress
A- SIZE, SHAPE AND TOPOLOGY OPTIMIZATION FOR 10-BAR PLANE TRUSS .

29. A- SIZE, SHAPE AND TOPOLOGY OPTIMIZATION FOR 10-BAR PLANE TRUSS .

30. Member Area (in2) Length (in) Weight (lb.) Axial Force (lb.) Stress Abs. value (KSI)
1,2 0.1 75.00 0.75 -7.00 0.07
2,6 0.3 130.50 3.92 3,815.00 12.72
1,5 0.3 130.50 3.92 3,120.00 10.40
2,3 0.3 130.50 3.92 709.00 2.36
1,4 0.3 130.50 3.92 1,014.00 3.38
1,6 3.6 106.80 38.45 55,766.00 15.49
1,3 3.6 106.80 38.45 10,236.00 2.84
2,5 3.6 106.80 38.45 45,923.00 12.76
2,4 3.6 106.80 38.45 15,032.00 4.18
6,5 1.7 75.00 12.75 -6,731.00 3.96
3,4 1.7 75.00 12.75 3,113.00 1.83
5,4 0.1 75.00 0.75 -1,222.00 12.22
6,3 0.1 75.00 0.75 -1,801.00 18.01
4,9 0.8 181.14 14.49 743.00 0.93
5,8 0.8 181.14 14.49 -3,304.00 4.13
6,7 0.8 181.14 14.49 -4,616.00 5.77
3,10 0.8 181.14 14.49 1,350.00 1.69
6,9 0.4 181.14 7.25 -2,308.00 5.77
5,10 0.4 181.14 7.25 -1,652.00 4.13
4,7 0.4 181.14 7.25 372.00 0.93
3,8 0.4 181.14 7.25 675.00 1.69
5,9 3.6 133.46 48.05 -20,181.00 5.61
6,10 3.6 133.46 48.05 -28,191.00 7.83
4,8 3.6 133.46 48.05 4,539.00 1.26
3,7 3.6 133.46 48.05 8,243.00 2.29
Weight (lb.) 476.337 Max Stress 18.01
Max. actual deflection absolute value is 8.8002
mm at node 1 in Y direction which represents
98.87% of allowable deflection.
Max. actual stress absolute value is 124.17 MPA
(18.01 KSI) in member 6,3 which represents
45.02% of allowable stress.
B- SIZE OPTIMIZATION FOR 25-BAR SPACE TRUSS.

31. B- SIZE OPTIMIZATION FOR 25-BAR SPACE TRUSS.

32. C- SIZE, SHAPE AND TOPOLOGY OPTIMIZATION FOR 25-BAR SPACE TRUSS.
The size, shape and topology optimization simultaneously will be considered with same data
input and constrains. For shape optimization case the coordinates limits for free node number 4
in X-direction From 20 to 60 inch and in Y-direction from 40 to 80 inch and in Z-direction from 90
to 130 inch where another free nodes 3,5 and 6 are symmetric to node number 4. And for
support node number 8 in X-direction From 40 to 80 inch and in Y-direction from 100 to 140
where another support nodes 7,9 and 10 are symmetric to node number 8.
Max. actual deflection absolute value is 8.8889 mm at node 1 in Y
direction which represents 99.87% of allowable deflection.
Max. actual stress absolute value is 119.62 MPA (17.35 KSI) in member
2,5 which represents 43.73% of allowable stress .
Member Area (in2) Length (in) Weight (lb.) Axial Force (lb.) Stress Abs. value (KSI)
1,2 Removed
2,6 0.10 123.76 1.24 844.30 8.44
1,5 0.10 123.76 1.24 1,549.30 15.49
2,3 0.10 123.76 1.24 748.60 7.49
1,4 Removed
1,6 0.90 96.06 8.65 12,136.50 13.49
1,3 0.90 96.06 8.65 7,639.20 8.49
2,5 0.90 96.06 8.65 15,618.60 17.35
2,4 0.90 96.06 8.65 6,334.20 7.04
6,5 Removed
3,4 Removed
5,4 Removed
6,3 Removed
4,9 0.10 233.70 2.34 351.30 3.51
5,8 0.10 233.70 2.34 72.70 0.73
6,7 0.10 233.70 2.34 193.50 1.94
3,10 0.10 233.70 2.34 398.90 3.99
6,9 0.10 176.71 1.77 255.90 2.56
5,10 0.10 176.71 1.77 96.10 0.96
4,7 0.10 176.71 1.77 464.70 4.65
3,8 0.10 176.71 1.77 527.60 5.28
5,9 1.00 148.65 14.87 1,142.00 1.14
6,10 1.00 148.65 14.87 3,042.00 3.04
4,8 1.00 148.65 14.87 5,524.00 5.52
3,7 1.00 148.65 14.87 6,272.00 6.27
Weight (lb.) 114.171 Max Stress 17.35

33. C- SIZE, SHAPE AND TOPOLOGY OPTIMIZATION FOR 25-BAR SPACE TRUSS.

34. Load Case 1 Max. actual deflection absolute value is 6.3 mm for node 17 in
X and Y direction which represents 99.21 % of allowable
deflection.
Max. Stress absolute value is 111.6 MPA (16.186 KSI) for
member 55 which represent 64.74% of allowable stress.
C- SIZE OPTIMIZATION FOR 72-BAR SPACE TRUSS BENCHMARK .

35. Load case 2 Max. Stress absolute value is 4.206/0.1733 = 24.27 KSI for
members 55, 56, 57 and 58 which represent 97.08% of
allowable stress.
Max. Stress absolute value is 0.99949 mm for nodes 17, 18, 19
and 20 in X and Y directions which represents 15.74 % of
allowable deflection.
C- SIZE OPTIMIZATION FOR 72-BAR SPACE TRUSS BENCHMARK .

36. C- SIZE OPTIMIZATION FOR 72-BAR SPACE TRUSS BENCHMARK .