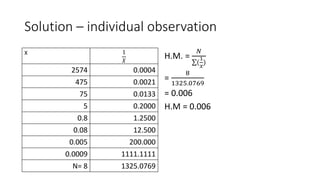
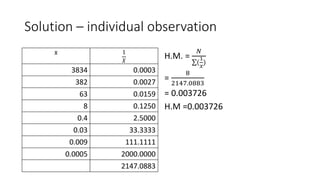
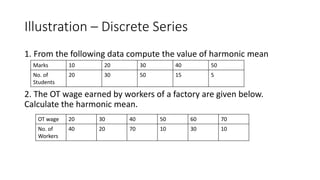
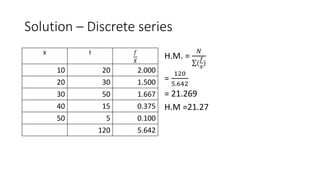
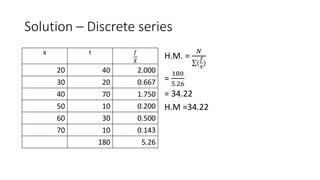
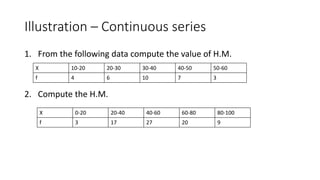
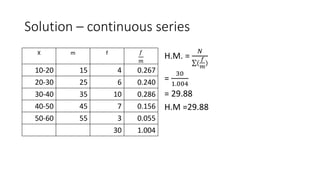
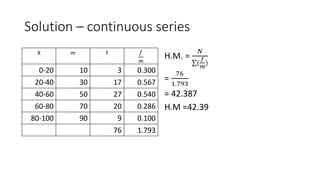
The document defines and provides examples of calculating the harmonic mean. The harmonic mean is based on the reciprocals of numbers. It is calculated as the reciprocal of the arithmetic mean of the reciprocals of the individual observations or data points. Examples are provided for calculating the harmonic mean of individual observations, discrete data series, and continuous data series. The harmonic mean provides an average rate for data expressed as proportions or rates.

1. Harmonic Mean
Dr. RMKV
SBKC

2. Harmonic Mean
• Is based on the reciprocals of numbers
• Is defined as the reciprocal of the arithmetic mean
• Individual observation H.M. =
𝑁
(
1
𝑥
)
• Discrete series H.M. =
𝑁
(
𝑓
𝑥
)
• Continuous series H.M. =
𝑁
(
𝑓
𝑚
)

3. Illustration – Individual Observation
1. Find the Harmonic Mean from the following :
• 2574,475,75,5, 0.8,0.08, 0.005, 0.0009
2. Calculate Harmonic mean from the following data:
• 3834,382,63,8,0.4,0.03,0.009,0.0005

4. Solution – individual observation
X 1
𝑋
2574 0.0004
475 0.0021
75 0.0133
5 0.2000
0.8 1.2500
0.08 12.500
0.005 200.000
0.0009 1111.1111
N= 8 1325.0769
H.M. =
𝑁
(
1
𝑥
)
=
8
1325.0769
= 0.006
H.M = 0.006

5. Solution – individual observation
X 1
𝑋
3834 0.0003
382 0.0027
63 0.0159
8 0.1250
0.4 2.5000
0.03 33.3333
0.009 111.1111
0.0005 2000.0000
2147.0883
H.M. =
𝑁
(
1
𝑥
)
=
8
2147.0883
= 0.003726
H.M =0.003726

6. Illustration – Discrete Series
1. From the following data compute the value of harmonic mean
2. The OT wage earned by workers of a factory are given below.
Calculate the harmonic mean.
Marks 10 20 30 40 50
No. of
Students
20 30 50 15 5
OT wage 20 30 40 50 60 70
No. of
Workers
40 20 70 10 30 10

7. Solution – Discrete series
X f 𝑓
𝑋
10 20 2.000
20 30 1.500
30 50 1.667
40 15 0.375
50 5 0.100
120 5.642
H.M. =
𝑁
(
𝑓
𝑥
)
=
120
5.642
= 21.269
H.M =21.27

8. Solution – Discrete series
X f 𝑓
𝑋
20 40 2.000
30 20 0.667
40 70 1.750
50 10 0.200
60 30 0.500
70 10 0.143
180 5.26
H.M. =
𝑁
(
𝑓
𝑥
)
=
180
5.26
= 34.22
H.M =34.22

9. Illustration – Continuous series
1. From the following data compute the value of H.M.
2. Compute the H.M.
X 10-20 20-30 30-40 40-50 50-60
f 4 6 10 7 3
X 0-20 20-40 40-60 60-80 80-100
f 3 17 27 20 9

10. Solution – continuous series
X m f 𝑓
𝑚
10-20 15 4 0.267
20-30 25 6 0.240
30-40 35 10 0.286
40-50 45 7 0.156
50-60 55 3 0.055
30 1.004
H.M. =
𝑁
(
𝑓
𝑚
)
=
30
1.004
= 29.88
H.M =29.88

11. Solution – continuous series
X m f 𝑓
𝑚
0-20 10 3 0.300
20-40 30 17 0.567
40-60 50 27 0.540
60-80 70 20 0.286
80-100 90 9 0.100
76 1.793
H.M. =
𝑁
(
𝑓
𝑚
)
=
76
1.793
= 42.387
H.M =42.39