A queue is a first-in, first-out (FIFO) data structure where items are inserted at one end and removed from the other. The document discusses different implementations of queues including physical, single-step append-serve, and circular queue models. It also covers priority queues where items are served based on priority level. An example application using queues to simulate airport arrivals and departures is provided. Key queue operations like append, serve, isEmpty and isFull are implemented in C++ using templates.

1. QUEUE

2. QUEUE
A queue is two ended data structure in which
items can be inserted from one end and taken out
from the other end. Therefore , the first item
inserted into queue is the first item to be taken out
from the queue. This property is called First in
First out [FIFO].

3. Queue Example
● A queue of people in the bank who are
trying to submit utility bills.
● A line of vehicle on the motorway toll plaza.
● Consider a shared printer in a computer
laboratory. Student can send their print
request to the printer and each print
request goto queue and serve one by one.
● Computer input operations performing
through mouse and keyboard are also
recorded into queue and serve on the basis
of FIFO.

4. Queue Operations
● Rear: is the tail/bottom of the queue. The entry at rear is the most
recently arrived item and must wait until the other entries are
present in the queue.
● Front: is the position from where items can be taken out from
queue. It is also termed as head or top of the queue. The entry at the
front position is ready to be served.
● Append: The operation to add an item at the rear position of the
queue is termed as append or enqueue. We can append items at the
rear position of the queue until the queue is not full. The rear points
towards the position where new item has been appended.
● Serve: The operation to remove an item from the front position of
the queue is termed as server or dequeue. We can serve the items in
the queue until the queue is not empty. The front points towards the
position from where the available item can be severed

5. Queue Operations
● IsEmpty: Queue is consider empty when there is no item on
front of the queue. IsEmpty operation checks for this condition and
return true if the queue is empty else return false.
● IsFull: If no element can be appended at rear of the queue then
queue consider as full. When rear of the queue reaches this limit,
then queue is full and the IsFull operation return true else return
false.

6. Abstract DataType of Queue
● Data/Attributes/Values:
int size; //maximum elements that queue can accommodate.
– int Front; //ready to serve position.
– int Rear; //last appended item position.
– Type Items; //Items that the queue can handle.
● Functions/Operations:
– CreateQueue(int size);
● Create queue that can contain size items.
– Void Append(Type n);
● Condition: queue is not full, then append at rear position.
– Type Server( );
● Condition: queue is not empty then return the front item.

7. Abstract DataType of Queue
● Functions/Operations:
– Int IsEmpty( );
● return true if queue is empty else return false.
– Int IsFull( );
● Return true if queue is full else return false.

8. Queue Physical Model
● Items A Z C D E

9. Queue Physical Model
● Items A Z C D E

10. Queue Physical Model
● Items A Z C D E

11. Queue Physical Model
● Items A Z C D E

12. Queue Physical Model
● Items A Z C D E

13. Queue Implementation In C++
● Template <class AnyType>
● Class Queue {
● Private:
– Int Size, Rear, Front;
– AnyType* Items;
● Public:
– Queue( ) { //default constructor
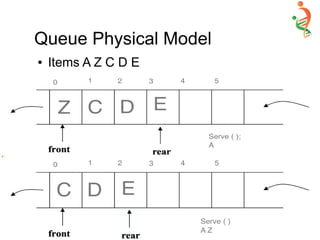
– Size =50; Rear = -1; Front = 0 //Front =0 is constant is Physical Model
– Items = new AnyType[Size];
● }
● Queue(int size) {
– Size=size; Rear = -1; Front = 0;
– Items = new AnyType[Size];
}

14. Queue Implementation In C++
● ~Queue ( ) {
– Delete [ ] Items; }
● Void Append (AnyType newItem) {
– If (!IsFull( ) )
● Items[++Rear ] = newItem;
– else
● Cout << “n Queue is Full … Append Failed”; }
● AnyType Server (void) {
– If (!IsEmpty ( ) )
● AnyType item =Item [Front]; // Same as item =item[0]
● for ( int i=0; i<Rear; i++ ) //Move each item one step forward
– Items[i] =Items [i+1];
● Rear --;
● Return item; }
– else
● Cout << “n Queue is empty … Serve failed”; }

15. Queue Implementation In C++
● Int IsEmpty ( ) { return (Rear == -1 ) ; }
● Int IsFull ( ) { return (Rear == (Size-1) ); }
● Void Display( ) {
● Cout<< “n”;
● If (IsEmpty( ) )
– cout<<”Empty”;
● Else
– for(int i=Rear; i>=Front; i—)
● cout<<Items[i]<< “ “;
● }
● }; //end physical Model Queue class

16. Queue Implementation In C++
● Void main( )
● { Queue<char> q(8);
● q.Display( );
● q.Append('A'); q.Display( );
● q.Append('C'); q.Display( );
● q.Serve( ); q.Display( );
● q.Append('G'); q.Display( );
● q.Append('D'); q.Display( );
● q.Append('M'); q.Display( );
● q.Serve( ); q.Display( );
● q.Append('Q'); q.Display( );
● q.Append('Z'); q.Display( );
● q.Append('R'); q.Display( );
● q.Serve();
● q.Append('J'); q.Display( );
● q.Append('H'); q.Display( );
● q.Append('W'); q.Display( );
● q.Append('E'); q.Display( );
● q.Serve( ); q.Display ( );
● getch( );
● }

17. Physical Model
Action Queue (Rear ← → Front ) Rear Front
Initial Empty -1 0
Append('A') A 0 0
Append('C') C A 1 0
Serve( ); C 0 0
Append('G') G C 1 0
Append('D') D G C 2 0
Append('M') M D G C 3 0
Serve( ); M D G 2 0
Append('Q') Q M D G 3 0
Append('Z') Z Q M D G 4 0
Append('R') R Z Q M D G 5 0
Serve( ); R Z Q M D 4 0
Append('J') J R Z Q M D 5 0
Append('H') H J R Z Q M D 6 0
Append('W') W H J R Z Q M D 7 0
Append('E') Queue Full … Append failed 7 0
Serve( ); W H J R Z Q M 6 0

18. Disadvantage of Physical Model
Queue
● On each server operation requires n move
operations, so that time efficiency of this
model is poor.
● To remove this poor efficiency while serve
is called “Single-Step Append-Serve
Model”. In this mode both rear and append
move.

19. Single Step Append-Serve Model
Action Queue (Rear ← → Front ) Rear Front
Initial Empty -1 0
Append('A') A 0 0
Append('C') C A 1 0
Serve( ); C 1 1
Append('G') G C 2 1
Append('D') D G C 3 1
Append('M') M D G C 4 1
Serve( ); M D G 4 2
Append('Q') Q M D G 5 2
Append('Z') Z Q M D G 6 2
Append('R') R Z Q M D G 7 2
Serve( ); R Z Q M D 7 3
Append('J') Queue Full … Append Fail 7 3
Append('H') Queue Full … Append Fail 7 3
Append('W') Queue Full … Append Fail 7 3
Append('E') Queue Full … Append Fail 7 3
Serve( ); R Z Q M 7 4

20. AnyType Serve(void) {
if(!IsEmpty( ) )
Return Items[Front++] ;
else
cout<<”Queue is Empty... Serve failed”;
}
– int IsEmpty() { return (Front > Rear ); }
– Int IsFull( ) { return (Rear == (Size-1) }
Single Step Append-Serve Model
Implementation

21. Disadvantage of Single Step
Append-Serve Model
Although time efficiency of single step
append-serve mode is good and no need
to move n element on each serve but
space utilization is poor.

22. Circular Queue
● The solution of append-serve model is
circular queue.

23. Circular Queue Implementation
● AnyType Append(AnyType new Item) {
If (!IsFull() ) {
Rear++
if(Rear == Size)
Rear=0;
Items[Rear]= newItem;
}
else
cout<<”Queue is full … Append failed.”;
}

24. Circular Queue Implementation
● AnyType Serve(void) {
If (!IsEmpty( ) {
AnyType item =Items[Front];
Front++;
If (Front ==Size)
Front=0;
Return item;
}
else
cout<<”Queue is Empty … serve failed”;

25. Circular Queue Implementation
● Int IsEmpty( ) {
Return (Front==NextPos(Rear) ); }
● Int Is Full() {
Return (Front ==NextPos(Nextpos(Rear)) ); }
● Int NextPos(int r ) {
r++;
if(r ==size)
r=0;
Return r;
}

26. Circular Queue Append-Serve Model
Action Queue (Rear ← → Front ) Rear Front
Initial Empty -1 0
Append('A') A 0 0
Append('C') C A 1 0
Serve( ); C 1 1
Append('G') G C 2 1
Append('D') D G C 3 1
Append('M') M D G C 4 1
Serve( ); M D G 4 2
Append('Q') Q M D G 5 2
Append('Z') Z Q M D G 6 2
Append('R') R Z Q M D G 7 2
Serve( ); R Z Q M D 7 3
Append('J') J R Z Q M D 0 3
Append('H') H J R Z Q M D 1 3
Append('W') Queue Full … Append Fail 1 3
Append('E') Queue Full … Append Fail 1 3
Serve( ); H J R Z Q M 1 4

27. Circular Queue Append-Serve Model
Action Queue (Rear ← → Front ) Rear Front
Serve( ); H J R Z 1 6
Serve( ); H J R 1 7
Serve( ); H J 1 0
Serve( ); H 1 1
Serve( ); Empty 1 2
Serve( ); Queue Empty … Serve Failed 1 2

28. Queue Application – Airport Simulation
Random Arrivals and
TakeOff
Results & comments Landing
(Rear ← → Front )
Takeoff
(Rear ← → Front)
Initial Simulation start Empty Empty
Landing.Append('G') Plane G Arrive for landing G Empty
Takeoff.Append('K') Plane K Arrive for Take-off G K
Landing.Append('Q') Plane Q Arrive for landing Q G K
Landing.Serve( ) Plane G landed Q K
Takeoff.Append('C') Plane C Arrive for Take-off Q C K
Landing.Append('R') Plane R Arrive for landing R Q C K
Landing.Serve( ) Plane Q landed R C K
Landing.Serve( ) Plane R landed Empty C K
Takeoff.Serve( ) Plane K Take off Empty C
Takeoff.Append('J') Plane J Arrive for Take-off Empty J C
Takeoff.Serve( ) Plane C Take off Empty J
Landing.Append('W') Plane W Arrive for landing W J
Takeoff.Append('K') Plane K Arrive for Take-off W K J
Landing.Serve( ) Plane W landed Empty K J
Takeoff.Serve( ) Plane J Take off Empty K
Takeoff.Serve( ) Plane K Take off Empty Empty

29. Priority Queue
● Priority queue is a data structure in which
items of the queue have priorities with
respect to each other. The items having
higher priority are served first and items
with lower priority are served later.
● Priority queue can implement on many
places e.g. On LAN shared printers print
request can print on the basis of priority.
Similarly Operating system has typically
queue of events. Each event has its own
priority and all event executed on their own
priority.

30. Priority Queue
● There are two type of priority queues
Minimum and Maximum.
● Minimum Priority Queue: A queue from
which the item that is minimum priority is
served first and the item having maximum
priority is served last.
● Maximum Priority Queue: A queue from
which the item that is maximum priority is
served first and the item having maximum
priority is served last.

31. Priority Queue ADT
Data/Attributes/Values
Int Size, Front, Rear;
Type Items;
Functions/Operations:
CreateQueue(int size);
//Create queue that can contain size items
Void place(Type n, int priority);
Condition: if queue is not full, then place at rear position w.r.t priority
For maximum priority queue the items with higher priorities are placed ahead of
lower priorities items and for minimum priority queue this is reverse.
● Type Serve( );
Condition: If queue is not empty then return the front item.
● Int IsEmpty ( ); Return 1 if queue is empty otherwise return 0
● Int IsFull( ); Return 1 if queue is full otherwise return 0

32. Priority Queue Implementation
# include <iostream.h>
● #include <conio.h>
● Template <class AnyType>
● Struct Item {
– AnyType Item;
– Int priority;
● Template <class AnyType>
● Class MaxPriorityQueue {
● private:
– int Size, Rear, Front;
– Item<AnyType>* Items;
● Public:
– MaxPriorityQueue ( ) //default constructor
– Size=50;
– Rear = -1
– Front = 0 //Always 0 in physical model
Items= new Item<AnyType>[Size];
}
● MaxPriorityQueue(int size) {
– Size = size;
– Rear = -1 ;
– Front = 0; //Always 0 in physical model
– Items = new Item<AnyType>[Size];
– }
● ~MaxpriorityQueue ( ) { delete[ ] Items; }
● Void Place(Item<AnyType> newItem) {
– if(IsEmpty( ) ) {
● Items [ ++Rear] = newItem;
– }
–

33. Priority Queue Implementation
if(!IsFull( ) ) {
Int i, putAt;
– For (i=Rear; i>=Front; i - - ) //Find where to
put item
if(newItem.priority <= Item[i].priority )
Break;
– PutAt=++ i //position where to put new item
– Rear ++;
– For (i=Rear; i>putAt; i-- ) //move item to
create space
● Item[i]=Items[ i -1];
– Items[putAt] = newItem;
– }
– Else
● cout<< “n Priority queue is Full. Place
failed “
● } // ending “} “ of place function
AnyType Serve(void) {
– if(!IsEmpty ( ) ) {
● AnyType item=Items[Front].Item;
● //same as item = item[ 0 ]
● for(int i=0; i<Rear; i++)
– Items[i] =Items[ i+1];
● Rear--;
● return item;
}
– else
– cout<<”nQueue is Empty... Serve failed”;
– }
– Int IsEmpty ( ) { return (Rear ==-1); }
– Int IsFull ( ) {return (Rear == (Size-1 ) ); }
– void Display( ) {
– cout<<endl <<Front<<' ' <<Rear<<' ' << “ “;
– If (IsEmpty( ) )
● cout<<”Empty”;

34. Priority Queue Implementation
– void Display( ) {
– cout<<endl <<Front<<' ' <<Rear<<' ' << “ “;
– If (IsEmpty( ) )
● cout<<”Empty”;
– else
● for(int i<Rear; i>=Front; i—)
– cout<<Item[i].Item<< ' ';
– }
– }; //end Physical model max priority Queue
class
– void main( ) {
– MaxpriorityQueue<char> q(8);
– Item<char> Items[ ] = { {'A', 0}, {'C', 0}, {'G', 1},
{'D', 0}, {'M', 2}, {'Q', 1},
{'Z', 2}, {'R', 1}, {'J', 3},
{'H', 0}, {'W', 1},{'E', 2}};
q.Display ( );
q.Place(Items[0]); q.Display( );
q.Place(Items[1]); q.Display( );
q.Serve( ) ;
q.Place(Items[2]); q.Display( );
q.Place(Items[3]); q.Display( );
q.Place(Items[4]); q.Display( );
q.Serve( );
q.Place(Items[5]); q.Display( );
q.Place(Items[6]); q.Display( );
q.Place(Items[7]); q.Display( );
q.Serve( );
q.Place(Items[8]); q.Display( );
q.Place(Items[9]); q.Display( );
q.Place(Items[9]); q.Display( );
q.Place(Items[9]); q.Display( );
● q.Serve( );
● getch ( ); }

35. Max Priority Queue (Physical Model)
Action Max priority Queue
(Rear ← → Front )
Front Rear
Initial Empty 0 -1
Place (A, 0) A, 0 0 0
Place (c, 0) C,0 A,0 0 1
Serve ( ) C, 0 0 0
Place (G, 1) C,0 G,1 0 1
Place (D, 0) D,0 C,0 G,1 0 2
Place (M, 2) D,0 C,0 G,1 M,2 0 3
Serve( ) D,0 C,0 G,1 0 2
Place (Q, 1) D,0 C,0 Q,1 G,1 0 3
Place (Z, 2) D,0 C,0 Q,1 G,1 Z,2 0 4
Place (R, 1) D,0 C,0 R,1 Q,1 G,1 Z,2 0 5
Serve( ) D,0 C,0 R,1 Q,1 G,1 0 4
Place (J, 3) D,0 C,0 R,1 Q,1 G,1 J,3 0 5
Place (H, 0) H,0 D,0 C,0 R,1 Q,1 G,1 J,3 0 6
Place (W, 1) H,0 D,0 C,0 W,1 R,1 Q,1 G,1 J,3 0 7
Place (E, 2) Priority Queue is Full..Place Failed 0 7
Serve( ) H,0 D,0 C,0 W,1 R,1 Q,1 G,1 0 6