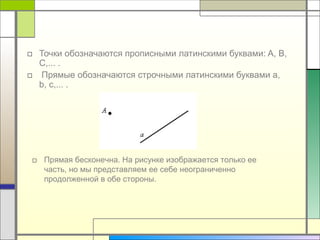
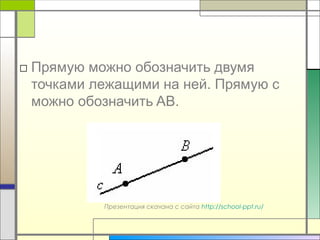
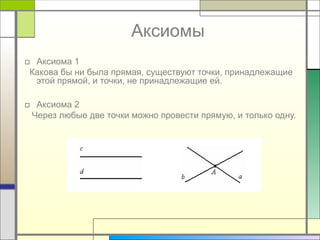
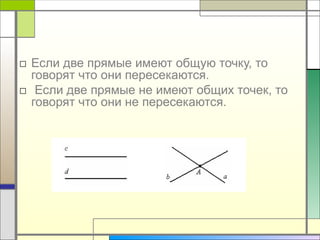
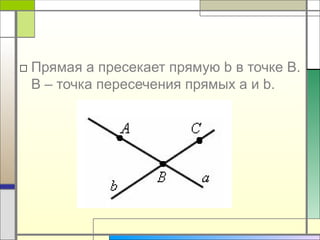
Документ описывает основные понятия геометрии, включая точки и прямые, их обозначения и аксиомы. Он утверждает, что через любые две точки можно провести одну и только одну прямую и объясняет понятия пересечения прямых. Также документ иллюстрирует, какие точки принадлежат или не принадлежат определенной прямой.

1. Прямая и точка
Основными геометрическими
фигурами на плоскости
являются точка и прямая.
Prezentacii.comPrezentacii.com

2. □ Точки обозначаются прописными латинскими буквами: A, B,
C,... .
□ Прямые обозначаются строчными латинскими буквами a,
b, c,... .
□ Прямая бесконечна. На рисунке изображается только ее
часть, но мы представляем ее себе неограниченно
продолженной в обе стороны.

3. □ Прямую можно обозначить двумя
точками лежащими на ней. Прямую с
можно обозначить AB.
Презентация скачана с сайта http://school-ppt.ru/

4. Аксиомы
□ Аксиома 1
Какова бы ни была прямая, существуют точки, принадлежащие
этой прямой, и точки, не принадлежащие ей.
□ Аксиома 2
Через любые две точки можно провести прямую, и только одну.

5. □ Если две прямые имеют общую точку, то
говорят что они пересекаются.
□ Если две прямые не имеют общих точек, то
говорят что они не пересекаются.

6. □ Прямая a пресекает прямую b в точке В.
В – точка пересечения прямых a и b.

7. □ Точки A и B принадлежат прямой a. Тоска С не принадлежит
прямой a.
□ Соответственно точки С и B принадлежат прямой b. Тоска A не
принадлежит прямой b.
□ Так же говорят точки A и B лежат на прямой a, а точка С не
лежит.